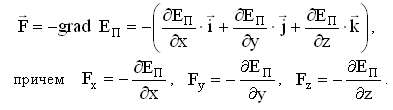2. Стационарное течение жидкости (газа). Линия тока. Трубка тока. Течение идеальной жидкости. Уравнение Бернулли. Условие применимости уравнения Бернулли.

Стационарным называется такой ток жидкости или газа, при котором конфигурация линий тока остаётся неизменной.

Линия тока – линия, касательная к которой всюду совпадает по направлению с вектором скорости частиц среды.

Трубка тока – это трубка, ограниченная линиями тока, столь малого сечения, в пределах которого скорости частиц среды одинаковы.

Течение идеальной жидкости:

Идеальной жидкостью называется воображаемая несжимаемая жидкость, в которой отсутствуют вязкость, внутренне трение и теплопроводность. Так как в ней отсутствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости. Рассмотрим течение идеальной жидкости внутри некоторой трубки тока, обладающей такими сечениями, что скорость молекул жидкости в любой точке каждого из них одинакова. Так как идеальная жидкость несжимаема, то ее масса, сосредоточенная между сечениями S1 и S2 трубки тока, с течением времени не изменяется. Поэтому объемы жидкости dQ, протекшие через эти сечения за промежуток времени dt, будут равны. Поскольку dQ = S·v·dt, то выполняется соотношение: S·v = const (1)

Это выражение называется уравнением неразрывности. Его физический смысл заключается в том, что жидкость нигде не накапливается, т. е. за одинаковый временной интервал в трубку тока втекает и вытекает равное количество жидкости.

Уравнение Бернулли: p + v²/2 + gh = const, всюду вдоль линии тока.

Применимо для:

1. линии тока

2. трубки тока

3. потока в целом (если в пределах любого сечения характеристики потока одинаковы)

4. для 2-х сечений при условии, что в пределах этих сечений характеристики потока одинаковы

Модель: жидкость несжимаема, трение отсутствует, ток стационарный.

p – статическое давление (измеряется монометрическим зондом)

v²/2 – динамическое давление (измеряется трубкой Пито)

p + v²/2 – полное давление (измеряется трубкой Пито)

gh – давление столба

Билет №8.

1. Работа силы. Консервативные силы. Энергия как запас работы. Кинетическая и потенциальная энергия системы материальных точек. Связь консервативных сил с потенциальной энергией. Закон сохранения механической энергии. Примеры его применения.

Элементарная работа силы F : dA(Fdr), где dr – элементарное перемещение точки приложения силы F.

_Работа силы F на участке s -

В физике консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.

Диссипативными называются такие силы, полная работа которых при любых движениях в замкнутой системе всегда отрицательна.

Потенциальными называют силы, работа которых по замкнутому контуру равна нулю.

Консервативные и потенциальные силы – одно и то же.

К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.

Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.

Консервативной называется система, в которой действуют только консервативные силы.

Так как работа консервативных сил зависит только от начального и конечного положения материальной точки, на которую они действуют, то их работа – это работа, совершаемая при изменении конфигурации тел, то есть изменение потенциальной энергии системы, взятое с обратным знаком. Примеры: сила упругости, сила тяжести, сила тяготения.

Закон сохранения механической энергии – механическая энергия системы тел сохраняется неизменной, если суммарная работа всех внешних сил и сил трения в системе равна нулю. Выводится из законов Ньютона. Пример применения: нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости (задача Х. Гюйгенса), машина Атвуда.

ЭНЕРГИЯ КАК ЗАПАС РАБОТЫ: Энергией называется одна из двух форм существования материи. Энергия эквивалентна величине запаса работы, как физического понятия, содержащейся в той или иной материальной системе. Энергией W называется способность тела совершать работу. Энергия — Способность тела совершать работу или запас работы. Любая работа, совершаемая над телом, увеличивает его энергию и делает его способным в свою очередь совершать работу.

Кинетической энергией системы называется скалярная величина Т, равная арифметической сумме кинетических энергий всех точек системы

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Потенциальная энергия системы. Для системы тел, в которой действуют только внутренние консервативные силы, можно ввести понятие потенциальной энергии. Силы, работа которых не зависит от формы перехода системы из начального положения в конечное, а определяется только начальной и конечной конфигурацией системы взаимодействующих тел, называются консервативными (потенциальными). Потенциальная энергия — скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Основная формула: E=mgh.

Связь консервативных сил с потенциальной энергией: Как потенциальная энергия может быть найдена по известной консервативной силе, так и консервативная сила может быть найдена по потенциальной энергии: