2. Гироскопические силы. Примеры гироскопических сил.

Гироскопическими силами называют силы упругости, действующие на опору со стороны быстро вращающихся масс.

Направление гироскопических сил можно легко найти с помощью правила, сформулированного Н.Е. Жуковским: гироскопические силы стремятся совместить момент импульса L гироскопа с направлением угловой скорости вынужденного поворота.

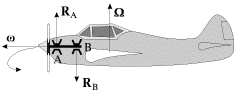
Пример 1. Легкий одномоторный самолет с правым винтом совершает левый вираж . Гироскопический момент передается через подшипники А и В на корпус самолета и действует на него, стремясь совместить ось собственного вращения винта (вектор w) с осью вынужденной прецессии (вектор ). Самолет начинает задирать нос кверху, и летчик должен "дать ручку от себя", то есть опустить вниз руль высоты. Таким образом, момент гироскопических сил будет компенсирован.

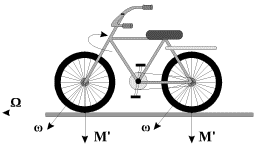
Пример 2. С гироскопическим эффектом мы сталкиваемся и при езде на велосипеде. Совершая, например, поворот направо, велосипедист инстинктивно смещает центр тяжести своего тела вправо, как бы заваливая велосипед. Возникшее принудительное вращение велосипеда с угловой скоростью приводит к появлению гироскопических сил с моментом .На заднем колесе этот момент будет погашен в подшипниках, жестко связанных с рамой. Переднее же колесо, имеющее по отношению к раме свободу вращения в рулевой колонке, под действием гироскопического момента начнет поворачиваться как раз в том направлении, которое было необходимо для правого поворота велосипеда.

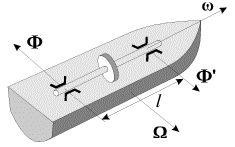
Пример 3. При килевой качке корабля (с носа на корму и обратно) ротор быстроходной турбины участвует в двух движениях: во вращении вокруг своей оси с угловой скоростью w и в повороте вокруг горизонтальной оси, перпендикулярной валу турбины, с угловой скоростью . При этом вал турбины будет давить на подшипники с силами лежащими в горизонтальной плоскости. При качке эти силы, как и гироскопический момент, периодически меняют свое направление на противоположное и могут вызвать "рыскание" корабля, если он не слишком велик (например, буксира).

Билет №3.

1. Понятие массы, импульса и силы в механике Ньютона. Законы Ньютона. Уравнение движения. Роль начальных условий.

Законы динамики – три закона Ньютона и законы, описывающие индивидуальные свойства сил. (см. гравитация, упругость, трение)

Всякое тело оказывает сопротивление при попытках изменить модуль или направление его скорости. Это свойство тел называется инертностью.

Инертная Масса – это мера инертности тела (при его поступательном движении).

Сила - любая причина, изменяющая импульс движущегося тела (мера взаимодействия).

Масса – одна из важнейших физических величин. Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. Тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — масса эквивалентна энергии покоя). (якобы неопределяемое понятие).

И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости.

I закон Ньютона – существуют такие системы отсчёта, в которых изолированное тело сохраняет состояние покоя или равномерного и прямолинейного движения.

II закон Ньютона – a = F / m, где F – равнодействующая сил, действующих на точку, a – ускорение точки, m – инертная масса точки.

III закон Ньютона – совокупность 5 утверждений:

1. силы взаимодействия в природе возникают парами

2. эти силы равны по величине

3. эти силы противоположны по направлению

4. эти силы действуют вдоль одной прямой

5. эти силы имеют одинаковую природу

Закон движения – зависимость координат точки от времени.

Уравнение движения – 2-й закон Ньютона записанный в виде F = m a, где F – равнодействующая сил, a – ускорение точки, m – инертная масса.

Основная задача механики состоит в том, чтобы, зная начальные условия, определить закон движения для тел системы.

Первый способ решения основной задачи механики состоит в том, чтобы найти закон движения, используя законы динамики.

Система законов, описывающих индивидуальные свойства сил, действующих в системе, подставленные в систему из уравнений движений элементов системы + уравнения кинематической связи дают систему дифференциальных уравнений, а законы движения для тел системы являются его решением. Отсюда очевидно, что задача не может быть решена если не известны начальные условия системы.

2. Основы механики деформируемых сред. Виды деформаций: упругие, остаточные, пластические. Классификация деформаций по геометрическому признаку. Деформации растяжения, сжатия, сдвига, кручения, изгиба.

Абсолютно твердым называется тело, конфигурация которого не меняется при любых воздействиях. Абсолютно упругим называется такое тело, у которого не остается деформации после снятия нагрузки.

Пластическим называется такое тело, у которого остаются деформации после снятия нагрузки

Закон Гука – деформация тела, если она достаточно мала, пропорциональна приложенной силе.

График зависимости деформации от силы сначала идёт по прямой, затем, начинает загибаться вверх (деформации ещё упругие), а потом идёт ещё круче вверх, переходя в зону пластических деформаций.

Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия(другими словами, атомы не выходят за пределы межатомных связей); в основе необратимых — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия.

Пластические деформации — это необратимые деформации, вызванные изменением напряжений. Деформации ползучести — это необратимые деформации, происходящие с течением времени. Способность веществ пластически деформироваться называется пластичностью. Остаточная деформация - деформация, которая после прекращения действий внешней силы сохраняется в деформируемом теле в виде пластической деформации (ИЛИ часть деформации, не исчезающая после устранения нагрузок и воздействий, вызвавших её).

Примеры деформаций.

Деформации можно измерять углами и смещениями, как абсолютно, так и относительно.

Деформации растяжения и сжатия. Если к однородному, закрепленному с одного конца стержню приложить силу F вдоль его оси в направлении от стержня, то он подвергнется деформации растяжения. Деформацию растяжения испытывают тросы, канаты, цепи в подъемных устройствах, стяжки между вагонами и т. д. Если на закрепленный стержень подействовать силой вдоль его оси по направлению к стержню, то он подвергнется сжатию. Деформацию сжатия испытывают столбы, колонны, стены, фундаменты зданий и т. п. При растяжении или сжатии изменяется площадь поперечного сечения тела.

Деформация сдвига. Деформацию сдвига можно наглядно продемонстрировать на модели твердого тела, представляющего собой ряд параллельных пластин, соединенных между собой пружинами. Горизонтальная сила F сдвигает пластины друг относительно друга без изменения объема тела. У реальных твердых тел при деформации сдвига объем также не изменяется. Деформации сдвига подвержены заклепки и болты, скрепляющие части мостовых ферм, балки в местах опор и др. Сдвиг на большие углы может привести к разрушению тела – срезу. Срез происходит при работе ножниц, долота, зубила, зубьев пилы и т. д.

Деформация изгиба. Легко согнуть стальную или деревянную линейку руками или с помощью какой-либо другой силы. Балки и стержни, расположенные горизонтально, под действием силы тяжести или нагрузок прогибаются – подвергаются деформации изгиба. Деформацию изгиба можно свести к деформации неравномерного растяжения и сжатия.

Деформация кручения. Если на стержень, один из концов которого закреплен, подействовать парой сил, лежащей в плоскости поперечного сечения стержня, то он закручивается. Возникает, как говорят, деформация кручения. Кручение испытывают валы всех машин, винты, отвертки и т. п.