Билет №21.
Вращение твёрдого тела вокруг неподвижной оси. Уравнение моментов. Плоское движение. Мгновенная ось вращения. Уравнение движения и уравнение моментов при плоском движении.
Вращение твердого тела:
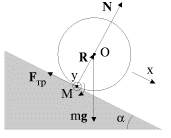Мгновенная
ось вращения проходит через точку
соприкосновения цилиндра и плоскости
(точку М). При таком подходе отпадает
необходимость в уравнении движении
центра масс и уравнении кинематической
связи. Уравнение моментов относительно
мгновенной оси имеет вид:
Здесь
В
проекции на ось вращения (ось y):
Ускорение
центра масс выражается через угловое
ускорение:
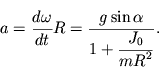
Уравнение
моментов:
Плоским называется такое движение твёрдого тела, при котором траектории всех его точек располагаются в параллельных плоскостях.
Мгновенной называется такая ось вращения, при помощи которой движение твердого тела в данное мгновение можно представить как только (чисто) вращательное.
Уравнение движения и уравнение моментов при плоском движении:
Движение
центра масс:
Ур-ние моментов:
Стоячие волны. Распределение амплитуд смещений, скоростей и ускорений «частиц» в стоячей волне. Узлы и пучности. Нормальные колебания стержня, струны, столба газа в трубе.
Уравнение плоской волны: y(x,t) = f(t- x/v) + f(t+x/v),
Стоячая волна – периодическое во времени синфазное колебание с характерным пространственным распределением амплитуды – чередованием узлов и пучностей.
В случае стоячей волны мех. энергия оказывается локализованной в промежутках между соседними узлами и пучностями, переходя из кинетической (в пучностях) в потенциальную (в узлах).
Варианты граничных условий:
закреплённая граница => узел
незакреплённая граница => пучность
Пучность — участок стоячей волны, в котором колебания имеют наибольшую амплитуду. Противоположностью пучности является узел — участок волны, в котором амплитуда колебаний минимальна.
Стоячие волны, волны, возникающие вследствие интерференции волн, распространяющихся во взаимно противоположных направлениях. Практически С. в. возникают при отражениях волн от преград и неоднородностей в результате наложения отражённой волны на прямую. Различные участки С. в. колеблются в одной и той же фазе, но с различной амплитудой (рис.). В С. в., в отличие от бегущей, не происходит течения энергии. Такие волны возникают, например, в упругой системе — стержне или столбе воздуха, находящегося внутри трубы, закрытой с одного конца, при колебаниях поршня в трубе. Бегущие волны отражаются от границ системы, и в результате наложения падающих и отражённых волн в системе устанавливаются С. в. При этом по длине воздушного столба образуются т. н. узлы смещений (скоростей) — плоскости, перпендикулярные к оси столба, на которых смещения частиц воздуха отсутствуют, а амплитуды давлений максимальны, и пучности смещений — плоскости, на которых смещения максимальны, а давления равны нулю. Узлы и пучности смещений располагаются в трубе на расстояниях четверти длины волны, причём у твёрдой стенки образуются всегда узел смещений и пучность давлений.
Нормальными называются такие колебания системы, при которых все части её колеблются по гармоническому закону с одинаковой частотой.
Условия нормальных колебаний струны, стержня, столба газа: L=kλ, или L=(k+1)(λ/2) (в зависимости от граничных условий).