2. Вектор Умова. Два вклада в энергию волны. Соотношения между ними.

Вектор Умова – вектор, направленный в сторону распространения волны и равный энергии волны, переносимой через единичную площадку в единицу времени

ω_кин=(1/2)ρ(∂ξ/∂x)²

ω_пот=(1/2)E(∂ξ/∂x)²

ω_кин = ω_пот.

p= 2 ω_кинv/v = ρ(∂ξ/∂x)² (∂x/∂t)v= -ρ (∂ξ/∂x) (∂ξ/∂t) v;

(∂ξ/∂x) (∂ξ/∂t) < 0

Билет №20.

1. Теорема Штейнера. Примеры её применения.

Теорема Штейнера: момент инерции твердого тела относительно некоторой произвольной оси равен сумме 2-х слагаемых:

1. момента инерции этого тела относительно оси, проходящей через его центр масс параллельно данной.

2. произведения массы тела на квадрат расстояния между осями.

Примеры: вычисление момента инерции тела относительно произвольной оси. (Момент инерции стержня относительно оси,проходящей через его край)

2. Отражение и преломление волн на границе раздела двух сред. Основные случаи граничных условий.

На примере распространения упругой волны на поверхности воды мы можем увидеть, как волна реагирует на корягу. Она отражается от коряги, часто возвращаясь в место броска камня. Причем, чем большего размера будет коряга, тем большая амплитуда волны отражается. Максимальная амплитуда отраженной волны будет при отражении от берега водоема. Т. е., измерив амплитуду отраженной волны, мы можем оценить размер отражающего объекта.

Поместим в водоем тонкостенную целлофановую емкость с другой жидкостью, например бензином, и возбудим волну в воде. Наблюдается интересный эффект. Дойдя до бензина, волна частично отражается от него, а частично переходит в целлофановую емкость. Оставляя емкость той же, и меняя жидкость, мы увидим, что амплитуда отраженных и прошедших в емкость волн будет различной. Отсюда следует фундаментальный вывод – амплитуды (энергии) отраженной от границы двух сред и прошедшей в другую среду зависит от характеристик этих сред. Эта характеристика называется акустическим сопротивлением (характеристическим импедансом) и для каждой среды описывается выражением z =rC (2.1), где r - плотность материала, а C - скорость упругой волны в этом материале.

Амплитуда (энергия) отраженной волны зависит также от формы отражающего тела и его расположения относительно распространяющейся волны. Если на поверхности воды расположить бревно так, чтобы оно отражало волну всей длиной, то амплитуда отраженной волны будет максимальной. Если бревно расположить длиной вдоль направления распространения волны, то амплитуда отраженной волны будет минимальной. Т. е. параметры отраженной волны определяются формой и расположением отражающего тела. Исследуя параметры отраженной волны, мы сможем определить форму дефекта. Это очень важно для оценки степени его опасности (обычно плоскостные дефекты типа трещин более опасны, чем округлые дефекты - поры).

В твердых телах картина отражения и прохождения упругих волн более сложная. Волны не только отражаются от границы раздела, но и преломляются и трансформируются (преобразуются из одного типа в другой). На рис.2.3 показана схема падения луча продольной волны под углом на границу раздела двух твердых сред.

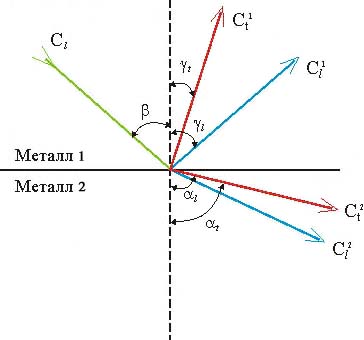
Видно, что от границы раздела отражается не одна, а две волны. Одна продольная, а другая сдвиговая (поперечная). Причем угол отражения продольной волны, как и в оптике, равен углу падения продольной волны. Сдвиговая волна отражается под другим углом.

Во вторую среду проходят также две волны. Продольная – с углом, отличным от угла падения, и сдвиговая, угол которой также отличается от угла отражения сдвиговой волны в первом твердом теле. Углы падения, отражения и преломления подчиняются закону Снеллиуса (закон синусов):

1. Импульсы, идущие «туда» и «обратно» не мешают друг другу.

2. Скорость «туда» такая же как «обратно».

3. Какими порциями энергия поступает к границе, где нет поглощения энергии, такими же она отправляется назад.

4. Энергия, которую несёт импульс не зависит от полярности, поскольку она пропорциональна квадратам деформации и скорости.

Варианты граничных условий:

1. закреплённая граница => узел

2. незакреплённая граница => пучность