Билет №18.

1. Динамика твёрдого тела. Момент силы. Момент импульса тела. Момент инерции тела относительно оси. Тензор инерции.

Динамика абсолютно твердого тела полностью определяется его полной массой, положением центра масс и тензором инерции (также, как динамика материальной точки — ее массой).

Момент силы— векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело: .

расстояние от точки, относительно которой рассматривается момент импульса.

Момент инерции тела относительно оси - величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равен сумме произведений элементарных масс dm всех малых частей тела на квадраты их расстояний r до рассматриваемой оси.

Тензор инерции — в механике абсолютно твёрдого тела — величина, связывающая момент импульса тела и кинетическую энергию его вращения с его угловой скоростью: .

Тензором инерции называется совокупность девяти величин, характеризующих инертные свойства твёрдого тела при его вращательном движении.

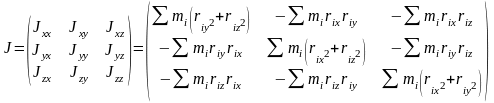
доказывается в лоб, раскрытием векторного произведения

Диагональные составляющие тензора – осевые моменты, остальные – центробежные.

2. Волновое уравнение. Решение волнового уравнения. Волны на струне, в стержне, газе. Связь скорости волны со свойствами среды. Поток энергии в бегущей волне.

Волновое уравнение:

Его решение: y(x,t) = f(t- x/v) + g(t+x/v), где f и g - произвольные дважды дифференцируемые по обеим переменным функции.

Волны на струне.

ρΔx =T(α+Δα) – Tα = TΔα= => =(T/ρ) ; α= => = (T/ρ) => (T/ρ)=v²

ρ – линейная плотность струны.

Продольные волны в твёрдом теле.

Ускорение частицы:

Получаем: , где ρ - плотность тела, E – модуль Юнга.

Продольные волны в газовой среде.

PV^γ=const, где γ≡c_p/c_v= (i+2)/i где i – количество степеней свободы частицы (для воздуха i=2)

∂PV^γ+PγV^γ-1∂V=0

dV/V=(-1/γP)dP сравнивая с = = получаем: v² = γP/ρ

Величина , (относительные значения диэлектрической и магнитной проницаемостей – в вакууме эпсилон=мю=1) определяющая изменение скорости света в среде по сравнению c вакуумом, называется абсолютным показателем преломления среды или оптической плотностью среды. Также известно как соотношение Максвелла, впервые установившего зависимость скорости электромагнитных волн от параметров среды их распространения.

Потоком энергии в бегущей волне называется мощность, перетекающая через единицу площади поверхности волнового фронта. В бегущей волне поток энергии равен модулю вектора Умова. Вектор Умова – вектор, направленный в сторону распространения волны и равный энергии волны, переносимой через единичную площадку в единицу времени.

Билет №19.

1. Главные, центральные, свободные оси вращения. Осевые и центробежные моменты инерции. Примеры.

Главной называется такая ось вращения твердого тела, в случае которой вектора угловой скорости и момента импульса коллинеарны.

Центральной называется такая ось вращения твердого тела, которая проходит через его центр масс.

Свободной называется такая ось вращения твердого тела (эквивалентные определения),

1. в случае которой равнодействующая всех центробежных сил инерции равна нулю и сумма моментов этих сил также равна нулю.

2. которая не испытывает деформирующего влияния со стороны центробежных сил инерции.

3. которая является одновременно главной и центральной

Тензором инерции называется совокупность девяти величин, характеризующих инертные свойства твёрдого тела при его вращательном движении.

доказывается в лоб, раскрытием векторного произведения

Диагональные составляющие тензора – осевые моменты, остальные – центробежные.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси: .

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).