2. Вынужденные колебания. Процесс установления колебаний. Резонанс. Амплитудная и фазовая резонансные характеристики колебательной системы. Добротность.

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:

Время релаксации - характерное время установления равновесия в системе.

Уравнение вынужденных колебаний: x’’+ 2γx’ + ω02x = f0 sin(ωt) (1)

Решение.

По прошествии времени релаксации: x =X sin (ωt+φ). X=? φ=?

x’ = ωXcos (ωt+φ); x’’ = -ω2 X sin (ωt+φ);

Подставляем в (1): -ω2 X sin (ωt+φ) + 2γ ωXcos (ωt+φ) + ω02 X sin (ωt+φ) = f0 sin(ωt)

При ωt = 0: -ω2 X sin (φ) + 2γ ωXcos (φ) + ω02 X sin (φ) = 0;

tg φ = -2γ ω/ ω02- ω2

1/sin2φ=1+ tg2 φ;

При ωt = π/2: 2γ ωX = - f₀ sin(φ);

X=- f0 sin(φ)/ 2γ ω;

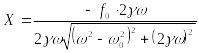
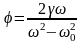
В общем виде x = X₀ e^-γt sin (ω₁t+φ) + X sin (ωt+φ).

Каковы бы ни были условия в момент начала действия внешней силы, осциллятор будет совершать одни и те же установившиеся гармонические колебания. Процесс установления колебаний называется переходным режимом. Он происходит потому, что с течением времени затухнут собственные колебания. Время установления колебаний определяется временем затухания колебаний, которые имелись в момент начала действия силы. Даже если начальных колебаний не было, то все равно время установления будет тем же.

Резонанс – резкое возрастание амплитуды вынужденных колебаний, когда частота вынуждающей силы приближается к частоте собственных колебаний системы.

ω² ≈ ω₀² => φ_x ≈ -π/2

Для вынужденных колебаний вводят, так называемые, амплитудно-частотные (зависимость амплитуды колебаний от частоты вынуждающей силы) и фазово-частотные (зависимость сдвига фаз от частоты вынуждающей силы) характеристики. Графически эти зависимости при различных значениях приведены на рисунках:

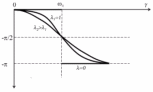
Добротность Q≡ = = 2π/(1-e^-2θ); при θ << 1, или δ << ω₀, Q=π/θ.

ω_рx²=ω₀²-2γ²

ω_рv²=ω₀²

ω_рa²=ω₀⁴/ ω₀²-2γ²

Произведение крайних равно квадрату средней.

X₀(ω=0) =F₀/k

A₀(ω=0) =F₀/m

Куда сдвигается, там и поднимается.

Билет №14.

1. Преобразования Лоренца. Инварианты преобразований Лоренца. Причинно-следственная связь между событиями.

Лоренца преобразования, в специальной теории относительности — преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой. Рассмотрим частный случай двух инерциальных систем отсчёта å и å’ с осями х и x’, лежащими на одной прямой, и соответственно параллельными другими осями (у и y’, z и z’). Если система å’ движется относительно å с постоянной скоростью u в направлении оси х, то Л. п. при переходе от å к å’ имеют вид:

, .

Лоренц-инвариантностью называют свойство какой-нибудь величины сохраняться при преобразованиях Лоренца (обычно имеется в виду скалярная величина).

Л. п. приводят к ряду важных следствий, в том числе к зависимости линейных размеров тел и промежутков времени от выбранной системы отсчёта, к закону сложения скоростей в теории относительности и др. При скоростях движения u<<c, Л. п. переходят в преобразования Галилея, справедливые в классической механике Ньютона.

Чтобы причинно-следственная связь имела объективный характер и не зависела от системы координат, в которой она рассматривается, необходимо, чтобы никакие материальные воздействия, осуществляющие физическую связь событий, происходящих в различных точках, не могли передаваться со скоростью, большей скорости света. Иначе говоря: причинно-следственная связь может иметь место, если s² > 0. в силу инвариантности интервала.