Раздел 2 .Математическая статистика

2 Выборочный метод.

2.1.1. Задачи математической статистики

Основная задача математической статистики состоит в установлении распределения реальной случайной величины или ее числовых характеристик по наблюденным значениям этой величины, причем используя не всю совокупность возможных значений (генеральную совокупность), а лишь часть ее – выборку.

Основные методы математической статистики:

Выборочный метод - основной метод математической статистики, состоящий в принятии статистических решений на основании выборки. Различают: - случай предварительного планирования объема выборки; - случай последовательного анализа, когда необходимый объем выборки выясняется в процессе эксперимента.

Конец формы

Дисперсионный анализ - предложенный Р.Фишером метод статистического анализа, позволяющий определить достоверность гипотезы о различиях в средних значениях на основании сравнения дисперсий распределений.

Начало формы

Конец формы

Канонический анализ - метод нахождения канонической корреляции, основанный на построении таких линейных комбинаций признаков (в двух заданных группах признаков), что обычный коэффициент парной корреляции между этими комбинациями достигает наибольшего значения.

Конец формы

Ковариационный анализ - совокупность методов математической статистики, предназначенных для выявления зависимости среднего значения некоторой случайной величины - от набора неколичественных факторов, задающих условия качественной природы, при которых получены наблюдения; и одновременно - от набора количественных факторов (сопутствующих переменных).

Конец формы

Корреляционный анализ - статистические методы обнаружения корреляционной зависимости между двумя или более случайными признаками или факторами.

Генеральная или выборочная совокупности

Генеральная совокупность - вся изучаемая выборочным методом статистическая совокупность объектов и/или явлений общественной жизни, имеющих общие качественные признаки или количественные переменные.

Выборочная совокупность (Выборка)- часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение о всей генеральной совокупности.

Для того, чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность выборка должна обладать свойством репрезентативности.

Вариационный ряд и полигон частот

Вариационный ряд - последовательность значений наблюденной величины, расположенных в порядке возрастания. Напр., вариационный ряд значений 1, - 3, 0, 5, 3, 4 имеет вид -3, 0, 1, 3, 4, 5. Вариационный ряд полностью определяется указанием различных значений входящих в него величин и числа членов ряда.

Полигон распределения частот случайной величины - графическое выражение распределения дискретной случайной величины; это — ломаная линия, координатами ее по оси X являются значения середин разрядов, в которые сгруппирована вся совокупность значений этой величины, а по оси У — частоты встречаемости значений, заключенных в пределах выделенных разрядов. Др. способ графического выражения этой величины — гистограмма.

Эмпирическая функция распределения и гистограмма

Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения x относительную частоту события X<x. Таким образом, по определению , где – число вариант, меньших x, n – объем выборки.

В отличие от эмпирической функции распределения выборки, функцию распределения генеральной совокупности называют теоретической функцией распределения. Различие между этими функциями состоит в том, что теоретическая функция определяет вероятность события X<x, тогда как эмпирическая – относительную частоту этого же события.

При росте n относительная частота события X<x, т.е. стремится по вероятности к вероятности этого события. Иными словами:

.

Гистограмма помимо эмпирических функций распределения, наглядное (но, вместе с тем, довольно приближенное) представление о неизвестном распределении можно получить при помощи гистограмм. Для построения гистограммы относительных частот на ось абсцисс наносим интервалы

[x_k-1 , x_k] и, используя каждый из них как основание, строим прямоугольник с соответствующей высотой H_k. Получаем гистограмму.

2.Статическое оценивание и проверка гипетез. Статические методы обработки эксперементальных данных.

2.2.1 Статистические оценки параметров распределения: генеральная средняя, выборочная средняя, генеральная дисперсия, выборочная дисперсия, исправленная дисперсия.

Основные требования к точечным оценкам параметров распределения.Несмещенность оценки. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности.

Состоятельность оценки. Оценка называется состоятельной, если она по вероятности с увеличением объема выборки п стремится к параметру генеральной совокупностиЭффективность оценки. Если составлять множество несмещенных и состоятельных оценок, то эти оценки будут иметь разные дисперсии. Ясно, что, чем меньше будет дисперсия, тем меньше будет вероятность грубой ошибки при определении приближенного параметра генеральной совокупности. Поэтому нужно выбрать такую оценку, у которой дисперсия была бы минимальной

Выборочная средняя дисперсия

Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения признака выборки различны, то

если же все значения имеют частоты n₁, n₂,…,n_k, то

Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней.

Замечание: Если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Выборочная дисперсия.

Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения , вводят сводную характеристику- выборочную дисперсию.

  Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения признака выборки различны, то

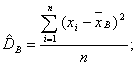
если же все значения имеют частоты n₁, n₂,…,n_k, то

Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:

Вычисление дисперсии- выборочной или генеральной, можно упростить, используя формулу:

Замечание: если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Исправленная дисперсия.

Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

 

Для исправления выборочной дисперсии достаточно умножить ее на дробь

получим исправленную дисперсию S². Исправленная дисперсия является несмещенной оценкой.

В качестве оценки генеральной дисперсии принимают исправленную дисперсию.

Для оценки среднего квадратического генеральной совокупности используют исправленное среднее квадратическое отклонение

Замечание: формулы для вычисления выборочной дисперсии и исправленной дисперсии отличаются только знаменателями. При достаточно больших n выборочная и исправленная дисперсии мало отличаются, поэтому на практике исправленной дисперсией пользуются, если n<30.

2.2.2. Интервальные оценки параметров нормального распредления

Интервальной называют оценку, которая определяется двумя числами—концами интервала, покрывающего оцениваемый параметр.

Понятия доверительного интервала и доверительной вероятности

Доверительным называют интервал, который с заданной надежностью  покрывает заданный параметр.

P(₁< < ₂) =P ((₁; ₂)) = 

Числа ₁ и ₂ называются доверительными границами, интервал (₁, ₂) — доверительным интервалом для параметра . Число  называется доверительной вероятностью или надежностью сделанной оценки.

Сначала задается надежность. Обычно ее выбирают равной 0.95, 0.99 или 0.999. Тогда вероятность того, что интересующий нас параметр попал в интервал (₁, ₂) достаточно высока. Число (₁ + ₂) / 2 – середина доверительного интервала – будет давать значение параметра  с точностью (₂ – ₁) / 2, которая представляет собой половину длины доверительного интервала.

Границы ₁ и ₂ определяются из выборочных данных и являются функциями от случайных величин x₁, x₂,..., x_n , а следовательно – сами случайные величины. Отсюда – доверительный интервал (₁, ₂) тоже случаен. Он может покрывать параметр  или нет. Именно в таком смысле нужно понимать случайное событие, заключающееся в том, что доверительный интервал покрывает число .

Доверительный интервал для оценки математического ожидания при известном s.

Известно среднее квадратическое отклонение этого распределения -s. Требуется оценить математическое ожидание а по выборочной средней ( ). Найдем доверительный интервал, покрывающий а с надежностью g. Выборочную среднюю будем рассматривать как случайную величину ( она изменяется от выборки к выборке), выборочные значения признака- как одинаково распределенные независимые СВ с математическим ожиданием каждой а и средним квадратическим отклонением s. Примем без доказательства, что если величина Х распределена нормально, то и выборочная средняя тоже распределена нормально с параметрами

Потребуем, чтобы выполнялось равенство

Заменив Х и s, получим

получим

Задача решена. Число t находят по таблице функции Лапласа Ф(х).