1.1.4.Формула полной вероятности

  Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно ,

 Применяя аксиому сложения вероятностей, имеем

   Но (i=1, 2, ..., n), поэтому

Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами».

Формула Байеса

Пусть событие происходит одновременно с одним из несовместных событий . Требуется найти вероятность события , если известно, что событие произошло.

На основании теоремы о вероятности произведения двух событий можно написать

Откуда

или 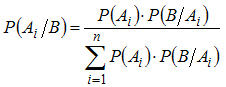(3.2)

Формула (3.2) носит название формулы Байеса.

Схема независимых испытаний по Бернулли

Проводится серия из nнезависимых испытаний, каждое из которых заканчивается либо “успехом” либо “неуспехом”, в каждом испытании (опыте) вероятность успеха p, а вероятность неуспеха q=1-p. Вероятность того, что в серии будет реализовано ровно k “успехов” вычисляется по формуле , где 0<p<1,k=0,1, …, n, , .

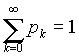Формулы Бернулли

Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность Pk,n того, что событие A наступит k раз в n независимых испытаниях, равна: ,

где q = 1-p

Локальная теорема Лапласа.

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

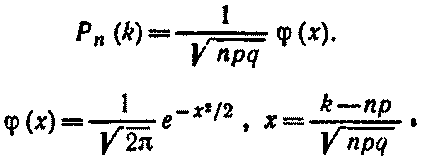
Для определения значений φ(x) можно воспользоваться специальной таблицей.

Интегральная теорема Лапласа.

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна

P(k₁;k₂)=Φ(x'') - Φ(x')

Здесь

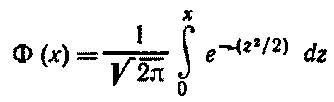
-функция Лапласа

Значения функции Лапласа находят по специальной таблице.

Теорема Пуассона

   При большом количестве испытаний вычисления по формуле Бернулли становятся затруднительными. Однако в ряде случаев их можно заменить более простыми асимптотическими формулами. Одна из них основана на теореме Пуассона.

Если число испытаний и так, что , , то при любых

Это означает, что при больших nи малых p вместо вычислений по точной формуле

можно воспользоваться приближенной формулой ,

т.е. использовать формулу Пуассона для  =np.

2.Случайные величины и законы их распределения

Понятие случайной величины.

Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.2 типа СВ: Дискретная-СВ,принимающая конечное или бесконечн.счетное множ-во значений. Например:частота попаданий при трех выстрелах;число бракованных изделий в партии из n штук; число вызовов, поступающих на телефон.станцию в течение суток; возможн.число горошин в 1 кг.

Непрерывная-СВ, кот. м.принимать люб.значения из некоторого конечн. или бесконечн.интервала.. Например: ошибка при измерении дальности радиолокатора;время безотказной работы микросхемы; погрешность изготовл-я деталей;концентрация соли в морской воде. Для задания случайной величины надо перечислить все ее возможн. значения и вероятности их появления. Совокупность всех возможн.знач-ий СВ и соответствующих им вероят-тей – распредел-е СВ.

Дискретные СВ- величина, кот.в рез-те испытаний принимает то или иное(только одно)возможн.значение,заранее неизвестное, меняющееся от испытания к испытанию и зависящее от случайн.обстоятельств. В отличие от случайн.события,кот. явл-ся качественной характеристикой случайн. рез-та испытания,случайн.величина характеризует рез-т испытания колич-но. Примеры: размер обрабатываемой детали,погрешность рез-та измерения к-л параметра изделия или среды.

Примеры распределений ДСВ:

Биномиальное распределение-распр-е кол-ва «успехов» в последоват-ти из n независимых случайн.экспериментов, таких что вероятность «успеха» в каждом из них одинакова.

фор-ла Бернулли: 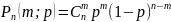, где p-вероят-ть,n-число испытаний, m-число появл-ий соб.А

Мат.ожид-е: 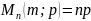, Дисперс.: 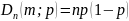прим. Вероятность поломки одного из пяти работающих независимо друг от друга станков = 0,2. Если происходит поломка, станок до конца дня не работает. Какова вероятность, что 0, 1, 2, 3, 4, 5 станков сломаются в течение дня?Решение:

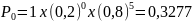
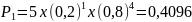и.т.д

Распред-е Пуассона-моделирует СВ, представляющую собой число событий, произошедших за фиксир-е время, при условии, что данные события происходят с нек. фиксиро-й средн.интенсивностью и независ.друг от друга (число испытаний 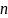-оч.велико, вероят.появл. соб. А-оч.мала) Фор-ла Пуассона: 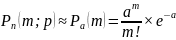(a=n*p)

Мат.ожид-е:

Дисперс.:

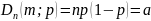
прим.:на АТС в теч-е 1 часа поступило n=500 сигналов.Вероят-ть сбоя p=0,002.Написать 5 первых членов закона распр-я.Решение:

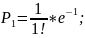
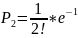и т.д.

Геометри́ч-е распред-е- распред-е дискретн.случайн. величины равной колич-ву испытаний случайн. эксперимента до наблюдения 1-го «успеха».

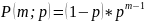где m-число испыт-ий

Мат.ожид-е:

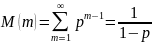
Дисперс.:

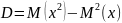
Прим.2стрелка поочерёдно стреляют по целям до 1-го попадания одного из орудий. Вероят-ть попадания 1-ым стрелком=0,7; 2-ым=0,8.Вначале стреляет 1-ый стрелок. Сост-ть 1-ые 5 членов распр-я. Реш-е: P(1)=0,7; Р(2)=0,3*0,8; Р(3)=0,3*0,2*0,7 и т.д.

Гипергеометрическое рас-е-моделирует кол-во удачных выборок без возвращения из конечн.совокупности.

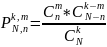Прим.В партии из N=20 изелий n=5 изд. имеют дефект.Какова вероят-ть,что из взятых m=4 изд. k=2 изд-я явл-ся дефектными? Реш.: