§15. Интервалы выпуклости и вогнутости.

Определение 1. F:y=f(x) направлена выпуклостью вверх или является выпуклой на некотором , если все точки,  graf, лежат ниже соответствующих точек,  касательным и построенным в  точке графика.

Определение 2. F:y=f(x) направлена выпуклостью вниз или является вогнутой на некотором интервале  если все точки графика этой функции лежат выше соответствующих им точек  касательным и построенным в  точке графика функции на этом интервале.

Теорема. Для того чтобы функция на некотором интервале была бы выпуклой необходимо чтобы f’’<0 во всех точках. 2)чтобы вогнутой – f’’>0.

Док-во. Необходимость. Пусть функция для определенности является выпуклой на некотором интервале, тогдапо определению каждая точка, принадлежащая графику, лежит ниже соответствующей точки, -ей касательной.

Т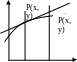 ак как уравнение касательной y-y₀=f(x₀)(x-x₀), где y₀=f(x₀), а из определений графика (х,у) связаны между собой следующими отношениями: x,y=f(x) условия соответствия точек можно переписать в виде y=f(x₀)+f’(x₀)(x-x₀)(для касательной) и y=f(x) – для точки  Y-y=f(x₀)-f(x)+f’(x₀)(x-x₀)=-f’()(x-x₀)+f’(x₀)(x-x₀)=-(f’()-f’(x₀))(x-x₀)=-f’’(ζ)(-х₀)(х-х₀). И при этом ζ,  и х₀ связаны между собой. Х₀ ζ  х.

Так как по предположению функция выпуклая, то У-у>0, что возможно, если f’’<0.

Док-во. Имея записанное выражение Y-y =f’’(ζ)(-х₀)(х-х₀), то f’’<0x-y>0функция выпуклая на рассматриваемом интервале, так как точка и касательная были выбраны произвольно.

Определение 1. хD₀(f)- точка перегиба, если она разделяет интервалы вогн. и выпукл.

Теорема 1. Если точка х – точка перегиба, то либо вторая производная равна 0 либо ∄.

Док-во. Пусть точка х- точка перегиба и функция непрерывна дифференцируема до 2-го порядка в окрестности этой точки, тогда по определению в левосторонней окрестности функция является выпуклой, а в правосторонней вогнутой  f_лев’’0, f_прав’’0. F’’ - limf_лев’’(∆x0,∆x<0)=limf_прав’’((∆x0,∆x>0).

Определение 2. Множество точек, где f’’=0 или ∄, называется множеством критических точек второго родав таких точках либо  точка перегиба, либо это некоторая особая точка функции.

Теорема о достаточном условии. Если х  К₂ и в окрестности указанной точки f’’ меняет свой знак, тогда эта точка и есть точка перегиба.

Билет 11(14).

§17. Ассимптотическое поведение функции. Ассимптоты графика.

Определение 1. Говорят что точка Г  графику функций, стремится вдоль графика на бесконечность, если lim длины радиуса-вектора этой точки есть +.

Определение 2. При х=а, где а может быть и не собственным, то есть (+-), линейно ассимптотическое поведение, если в окрестности указанной точки функция может быть представлена в виде f(x)=kx+b+(x), k,b-числа, (х)- б.м. в окрестности указанной точки.

Определение 3. Прямая с уравнением у=kx+b называется ассимптотой графика функции в окрестности той или иной точки, если при стремлении точки вдоль графика на бесконечность расстояние между соответствующей точкой  графику функции и указанной прямой есть б.м. но, другими словами если PGr(f), то имеет место соотношение limPP_P=0(P). P_p-прямой, кот. Явл. Ассимт.

1))) вертикальные ассимптоты.

Теорема . если х=а есть точка разрыва функции, то прямая с уравнением х=а является ассимптотой графика функции, которую принято называть вертикальной ассимптотой.

2)))Определение 3. При х+, x- у функции f:y=f(x) есть наклонная ассимптотаб если в окрестности бесконечно удаленной точки функция имеет линейное ассимптотическое представление, при этом р:кх+в – наклонная ассимптота.

Теорема 2. x+/- чтобы у функции была наклонная ассимптота необходимо и достаточно чтобы  два предела: limf(x)/x=k (x+) и limf(x)-kx=b (x+). Если первый lim ∄, то у функ. Нет ассим.

Док-во. Пусть при x+ у функции  наклонная ассимптотапри стремлении вдоль Gr на  в окрестности указанной бесконечно удаленной точки функция имеет aсс-ое линейное представление:f(x)=kx+b+(x)lim =[k+0+0]=k. Limf(x)-kx=limkx+b+(x)-kx=[b+a]=0. (x+)2) пусть  оба предела, тогда из limf(x)-(kx+b)(x+) следует, что limf(x)-(kx+b)=0f(x)-(kx+b)=(x)=[0]f(x)=kx+b+(x)(линейное асс-ое представление функциипрямая по определению р:у=кх+в – наклонная ассимптота.

Билет Ш(1).