§8. Производные и диф-лы высших порядков.

Определение 1. Пусть f:z=f(x,y), пусть  частные производные от указанных производных по переменным х и у называются частными производными второго порядка, если они  и при этом если частная производная берется по той же самой переменной, что ипроизводная первого порядка, то такие производные называются частными производными второго порядка, в противном–случае смешанными.

Определение 2. Частной производной п-того порядка называется производная 1-го порядка по производной (п-1) порядка, если они .

Теорема 1. О смешанной производной.

Если смешанные производные, вычесленные в разном порядке, являются непрерывными в окрестности рассматриваемой точки, то смешанная производная не зависит от порядка диф-ния.

Док-во. Пусть z=z(x,y) и в окрестности рассматриваемой точки  смешанные производные . Введем вспомогательную функцию: R(∆x,∆y)=z(x₀+∆x,y₀+∆y)-z(x₀+∆x,y₀)-z(x₀,y₀+∆y)+z(x₀,y₀)R(∆x,∆y)=z(x₀+∆x,y₀+∆y)-z(x₀+∆x,y₀)-(z(x₀,y₀+∆y)-z(x₀,y₀))=∆(x,y₀,y₀+∆y)=  (x)=z(x,y₀+∆y)-z(x,y₀) по теореме Лагранжа = (2)

R(∆x,∆y)=z(x₀+∆x,y₀+∆y)-z(x₀+∆x,y₀)-(z(x₀,y₀+∆y)-z(x₀,y₀))∆=z(x₀+∆x,y)-z(x₀y) (1). При ∆х, ∆у0 (1) и (2) совпадают.

Билет Ш(8).

§10. Loc и glob extr-мы функции нескольких действительных переменных.

Определение 1. Р₀ – точка loc extr и при этом является точкой loc min если U(P₀), что для всех точек изэтой окрестности имеет место неравенство f(P)-f(P₀)0; P_* называется точкой loc max если  U(P_*), чтл  PU(P_*)f(P)-f(P_*)0.

Определение 2. Точка Р₀ называется glob min в некотрой области , если : Р f(P)-f(P₀)0. Точка Р_* называется glob max в некотрой области , если : Р f(P)-f(P_*)0.

Теорема 1. О необходимом условии  loc extr-ма.

Если точка Р₀ является точкой loc extк f, то либо 1)df: (P₀)=0, и  одновременно обращаются в ноль частные производные 1-го порядка по независимым переменным, либо 2) хотя бы одна из частных производных в указанной точке ∄.

Док-во. Пусть f:z=f(x,y), тогда, если функция диф-ма в точке, то  производная по  направлению и в частности  частные производные z/x и z/y  по направлению O_x функция и её приращение относительно точки P₀ являются функциями лишь одной независимой переменной  по теореме о необходимом условии -ия loc extr функции одной действительной переменной z/x=0, а в случае недиф-ти ∄ вовсе. Аналогично по направлению О_у: либо z/y=0, либо в случае недиф-ти ∄ вовсе, а так как df(P₀)=(f/x)*∆x+(f/y)/∆y, то в случае диф-ти обе произв-ые равны нулю и тогда df(P₀)=0.

Билет Ш(9).

§11. Достаточные условия -ия loc extr в случае диф-емой функции двух независимых переменных.

Теорема 1. Если f:y=f(р) имеет в окрестности точки Р₀ все непрерывные производные до п-того порядка включительно, то в U(P₀) имеет место равенство f(P)=f(P₀+ , где ∆=Р_*Р(формула Тейлора п-того порядка).

Теорема 2. Пусть f:z=f(x,y). Пусть точка Р_оК₁, то есть множеству точек, в которых выполнены необходимые условия  loc extr. Пусть функция в окрестности этой точки имеет непрерывные вторые производные, тогда если если определитель , то Р₀ есть точка loc extr и при этом если a₁₁>0, то в точке имеется locmin, если же a₁₁<0в точке loc extr нет и точка является точкой minmax. Если определитель=0, то теорема ответа о характере точки не дает.

Док-во. В силу условий, указанных втеореме, df(P₀)0 формула Тейлора 2-го порядка в U(P₀) будет иметь вид f(x,y)=f(x₀,y₀)+ , или после элементарных перобразованийf(P)-f(P₀)= . Пусть определитель>0,a₁₁a₂₂-(a₁₂)²>0, тогда учитывая, что ∆x/∆=cosץ, ∆y/∆=sinץ, где

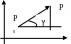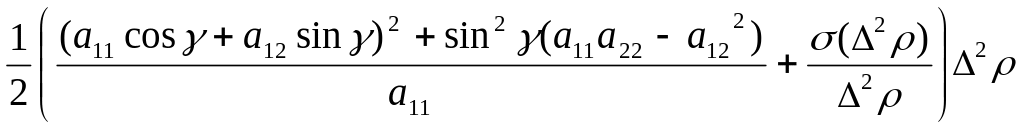И з последнего выражения для приращения функций  f(P)-f(P₀)= . Из полученной формулы для приращения тогда  что знак указанного приращения определяется знаком определителя, а так как по предположению определитель положителен, то если a₁₁>0, то знак будет положителен и f(P)-f(P₀)>0, то определитель точки P₀loc min. Аналогично, когда a₁₁<0.