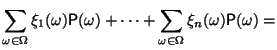- •5. Классическое определение вероятности:
- •6. Геометрическая вероятность.
- •7.Теорема сложения вероятностей несовместных событий.
- •8. Условная вероятность. Теорема произведения вероятностей зависимых событ.
- •9.Формула полной вероятности.
- •10.Формула Байеса.
- •12.Последовательность независимых испытаний. Формула Бернулли.
- •20Дисперсия
- •Случайные величины и законы их распределения
- •29.Неравенство Чебышева.
- •18.Математическое ожидание функции одного случайного аргумента.
- •[Править] Свойства независимых случайных величин
29.Неравенство Чебышева.
Неравенство Чебышева, используемое для доказательства дальнейших теорем, справед-ливо как для непрерывных, так и для дискретных случайных величин. Докажем его для дискретных случайных величин.
неравенство Чебышева.
p( | X – M(X)| < ε ) ≥ D(X) / ε². (13.1)
Доказательство. Пусть Х задается рядом распределения
Х |
х1 |
х2 |
… |
хп |
р |
р1 |
р2 |
… |
рп |
Так как события |X – M(X)| < ε и |X – M(X)| ≥ ε противоположны, то р ( |X – M(X)| < ε ) + + р ( |X – M(X)| ≥ ε ) = 1, следовательно, р ( |X – M(X)| < ε ) = 1 - р ( |X – M(X)| ≥ ε ). Найдем р ( |X – M(X)| ≥ ε ).
D(X) = (x1 – M(X))²p1 + (x2 – M(X))²p2 + … + (xn – M(X))²pn . Исключим из этой суммы те слагаемые, для которых |X – M(X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые k слагаемых. Тогда
D(X) ≥ (xk+1 – M(X))²pk+1 + (xk+2 – M(X))²pk+2 + … + (xn – M(X))²pn ≥ ε² (pk+1 + pk+2 + … + pn).
Отметим, что pk+1 + pk+2 + … + pn есть вероятность того, что |X – M(X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D(X) ≥ ε² р(|X – M(X)| ≥ ε), или р (|X – M(X)| ≥ ε) ≤ D(X) / ε². Тогда вероятность противоположного события p( | X – M(X)| < ε ) ≥ D(X) / ε², что и требо-валось доказать.
18.Математическое ожидание функции одного случайного аргумента.
Пусть Y = φ(X) – функция случайного аргумента Х, и требуется найти ее математическое ожидание, зная закон распределения Х.
1)Если Х – дискретная случайная величина, то
![]() (10.2)
(10.2)
2)Если Х – непрерывная случайная величина, то M(Y) можно искать по-разному. Если известна плотность распределения g(y), то
![]()
Если же g(y) найти сложно, то можно использовать известную плотность распределения f(x):
![]()
В частности, если все значения Х принадлежат промежутку (а, b), то
![]()
26.Корреляционным
моментом системы
двух случайных величин называется
второй смешанный центральный момент:
Kxy
= μ1,1
= M((X
– M(X))(Y
– M(Y))).
Для дискретных случайных величин
![]()
для
непрерывных случайных величин
![]() Безразмерной характеристикой
коррелированности двух случайных
величин является коэффи-циент
корреляции
Безразмерной характеристикой
коррелированности двух случайных
величин является коэффи-циент
корреляции
![]() .
Корреляционный момент описывает связь
между составляющими двумерной
случайной вели-чины. Действительно,
убедимся, что для независимых Х
и Y
Kxy
= 0. В этом
случае f(x,y)
= =f1(x)f2(y),
тогда
.
Корреляционный момент описывает связь
между составляющими двумерной
случайной вели-чины. Действительно,
убедимся, что для независимых Х
и Y
Kxy
= 0. В этом
случае f(x,y)
= =f1(x)f2(y),
тогда![]() Итак,
две независимые случайные величины
являются и некоррелированными. Однако
понятия коррелированности и зависимости
не эквивалентны, а именно, величины
могут быть зависимы-ми, но при этом
некоррелированными. Дело в том, что
коэффициент корреляции характеризует
не всякую зависимость, а только линейную.
В частности, если
Y
= aX
+ b,
то rxy
= ±1. Найдем
возможные значения коэффициента
корреляции.
Теорема
9.1.
Итак,
две независимые случайные величины
являются и некоррелированными. Однако
понятия коррелированности и зависимости
не эквивалентны, а именно, величины
могут быть зависимы-ми, но при этом
некоррелированными. Дело в том, что
коэффициент корреляции характеризует
не всякую зависимость, а только линейную.
В частности, если
Y
= aX
+ b,
то rxy
= ±1. Найдем
возможные значения коэффициента
корреляции.
Теорема
9.1.
![]() Доказательство.
Докажем сначала, что
Доказательство.
Докажем сначала, что
![]() Действительно, если рассмотреть
случай-ную величину
Действительно, если рассмотреть
случай-ную величину
![]() и найти ее дисперсию, то получим:
и найти ее дисперсию, то получим:![]() .
Так как дисперсия всегда неотрицательна,
то
.
Так как дисперсия всегда неотрицательна,
то
![]() откуда
Отсюда
откуда
Отсюда
![]() что и требовалось доказать.
что и требовалось доказать.
3.

4.


13. Теорема Пуассона
Если
число испытаний n
в схеме
независимых испытаний Бернулли стремится
к бесконечности и
![]() так,
что
так,
что
![]() ,
,
![]() ,
то при любых
,
то при любых
![]()
![]()
Это
означает, что при больших n
и малых p
вместо громоздких вычислений по точной
формуле
![]() можно
воспользоваться приближенной формулой
можно
воспользоваться приближенной формулой
![]() ,
т.е. использовать формулу Пуассона для
= np.
,
т.е. использовать формулу Пуассона для
= np.
2.Пространство
элементарных исходов
— множество исходов случайного
эксперимента;
обычно обозначается Ω,
а его элементы
![]() —
исходы случайного эксперимента —
называются элементарными
событиями;
одно из основных понятий теории
вероятностей.
Для случайных экспериментов «бросание
монеты» или «игральной кости» пространства
элементарных событий имеют вид Ω1
= {ω1,ω2},
где ω1
— «выпадение герба», ω2
— «выпадение решётки»; Ω2
= {ω1,ω2,ω3,ω4,ω5,ω6}где
ωn
— «выпадение n очков»
—
исходы случайного эксперимента —
называются элементарными
событиями;
одно из основных понятий теории
вероятностей.
Для случайных экспериментов «бросание
монеты» или «игральной кости» пространства
элементарных событий имеют вид Ω1
= {ω1,ω2},
где ω1
— «выпадение герба», ω2
— «выпадение решётки»; Ω2
= {ω1,ω2,ω3,ω4,ω5,ω6}где
ωn
— «выпадение n очков»
1. Теория вероятностей-раздел математики, изучающий в абстрактной форме реально существующие закономерностей случайных явлений. Возникла в 17 веке, в связи со след. прикладными задачами:
расчет вероятности в азартных играх,
задача теория стрельбы (сколько раз нужно выстрелить по цели, чтобы она была поражена с заданной вер-тью)
задача страхового дела (расчет страх. платежей, составление таблиц смертности)
задача демографии(во всех странах, рождаемость мальчиков 0,514)
задача теории ошибок наблюдения
Основоположники Ферма, Паскаль. Теория вероятностей развивалась в работах Лапласа, Вернули и др.(рус.-Чебышев, Марков, Ляпунов, Космогоров, Романовский и др.)Из теории вероятностей развилась мат статистика, теория игр, защиты инф-ии, массового обслуживания. Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах, относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Оказалось, что это постоянное число есть вероятность появления события.Таким образом, если опытным путем установлена относительная частота, то полученное число можно принять за приближенное значение вероятности.
21. Случайные векторы
Пусть на одном и
том же вероятностном пространстве (
![]() , F, P)
задано n
случайных величин
, F, P)
задано n
случайных величин
![]() ,
,
![]() ,
…,
,
…,
![]() .
Совокупность случайных величин
.
Совокупность случайных величин
![]() называется
многомерной
(n-мерной)
случайной
величиной,
или (n-мерным)
случайным вектором.
называется
многомерной
(n-мерной)
случайной
величиной,
или (n-мерным)
случайным вектором.
Пример 2.2.1. Широта
X
и долгота Y
падения метеорита на Землю представляют
собой двумерный случайный вектор
![]() .
В эту модель можно ввести также третью
координату Z
– время от начала наблюдений до момента
падения первого метеорита на Землю.
Тогда получится трехмерный случайный
вектор
.
В эту модель можно ввести также третью
координату Z
– время от начала наблюдений до момента
падения первого метеорита на Землю.
Тогда получится трехмерный случайный
вектор
![]() .
.
Пример 2.2.2. Успеваемость студента, окончившего курс обучения в вузе, характеризуется системой n случайных величин – оценками, проставленными в его дипломе.
22.
Если () — дискретный случайный вектор, то совместным распределением случайных величин и чаще всего называют таблицу вида
|
y1 |
y2 |
... |
ym |
x1 |
p11 |
p12 |
... |
p1m |
x2 |
p21 |
p22 |
... |
p2m |
... |
... |
... |
pij |
... |
xn |
pn1 |
pn2 |
... |
pnm |
где
![]() и
и
![]() .
.
По этой таблице можно найти распределение каждой из случайных величин и по формулам:
Случайные величины
называются независимыми,
если для
любых
![]() справедливо
справедливо
![]() .
.
Для того, чтобы рij были распределением
вероятностей дискретного случайного вектора
![]() ,
,
необходимо и достаточно выполнение условий :
![]()
![]()
Д о к а з а т е л ь с т в о
Докажем только необходимость. Для того, чтобы доказать достаточность нужно описать эксперимент, похожий на (15.2.2) .
Условие 1) очевидно необходимо.
Покажем, что события
Hij = {X1 = x1i}{X2 = x2j} (20.1.1)
образуют полную систему событий.
События Ai = {X1 = x1i} , i = 1…n , образуют полную систему и события
Bi = {X2 = x2j} , j = 1…m образуют полную систему. Имеем Hij = AiBj
Покажем, что они несовместны.
Пусть
![]() ,
т.е. хотя бы 1 из индексов не совпадает,
например,
,
т.е. хотя бы 1 из индексов не совпадает,
например,
![]()
![]()
Покажем, что их сумма - достоверное событие :
![]()
Отсюда следует, что
![]()
Что и требовалось доказать.
19.
Если случайная
величина
![]() постоянна,
то есть, для некоторой константы
постоянна,
то есть, для некоторой константы
![]() имеет
место
имеет
место
![]() ,
то
,
то
![]()
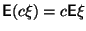 для
любого
для
любого
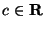 .
.
Если
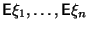 существуют,
то
существуют,
то
![]()
Если
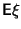 и
и
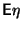 существуют
и
существуют
и
 для
всех
для
всех
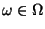 ,
то
,
то
![]()
В частности, если
![]()
![]() ,
то математическое ожидание
неотрицательно
при условии, что оно существует.
,
то математическое ожидание
неотрицательно
при условии, что оно существует.
Доказательство.
Свойства 1) и 2) очевидны. Докажем 3).
|
|
|
|
|
|
|
|
|
|
|
|
Докажем
4). Так как при каждом
![]() имеет
место
,
то
имеет
место
,
то

что влечет
![]() .
.
14 Если поток событий стационарен, ординарен и без последействий, то такой поток называется простейшим (пуассоновским) потоком.
Это название связано с тем, что в этом случае число событий, попадающих на любой фиксированный интервал времени, распределено по распределению Пуассона .
В соответствии с этим законом распределения математическое ожидание числа точек, попавших попадающих на участок времени t, имеет вид:
![]()
l - плотность потока – среднее число событий в единицу времени.
Вероятность того, что за время t произойдет ровно т событий, равна
![]() Вероятность
того, что в течение данного времени не
произойдет ни одного события, равна:
Вероятность
того, что в течение данного времени не
произойдет ни одного события, равна:
![]() Пусть
Т – промежуток времени между двумя
произвольными соседними событиями в
простейшем потоке. Найдем функцию
распределения
Пусть
Т – промежуток времени между двумя
произвольными соседними событиями в
простейшем потоке. Найдем функцию
распределения
![]() В
соответствии с законом распределения
Пуассона, получаем:
В
соответствии с законом распределения
Пуассона, получаем:
![]() Математическое
ожидание, дисперсия и среднее квадратическое
отклонение этой величины соответственно
равны:
Математическое
ожидание, дисперсия и среднее квадратическое
отклонение этой величины соответственно
равны:
![]() Таким
образом, для величины Т получили
показательный закон распределения
Таким
образом, для величины Т получили
показательный закон распределения
24.Пусть
![]() -
случайный вектор. Тогда по определению
-
случайный вектор. Тогда по определению
![]() ,
,
то есть математическое ожидание вектора определяется покомпонентно.
Ковариацио́нная ма́трица (или ма́трица ковариа́ций) в теории вероятностей — это матрица, составленная из попарных ковариаций элементов двух случайных векторов.
Пусть
![]() —
два случайных вектора размерности n
и m
соответственно. Пусть также случайные
величины
—
два случайных вектора размерности n
и m
соответственно. Пусть также случайные
величины
![]() имеют
конечный второй момент,
то есть
имеют
конечный второй момент,
то есть
![]() .
Тогда матрицей ковариации векторов
.
Тогда матрицей ковариации векторов
![]() называется
называется
![]() то
есть
то
есть
Σ = (σij),где
![]() .
.
Если
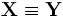 ,
то Σ
называется матрицей ковариации вектора
,
то Σ
называется матрицей ковариации вектора
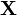 и
обозначается
и
обозначается
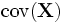 .
Такая матрица ковариации является
обобщением дисперсии
для многомерной случайной
величины,
а ее след — скалярным выражением
дисперсии
многомерной случайной
величины.
Собственные
векторы
и собственные
числа
этой матрицы позволяют оценить размеры
и форму облака распределения такой
случайной
величины,
аппроксимировав его эллипсоидом (или
эллипсом в двумерном случае).
.
Такая матрица ковариации является
обобщением дисперсии
для многомерной случайной
величины,
а ее след — скалярным выражением
дисперсии
многомерной случайной
величины.
Собственные
векторы
и собственные
числа
этой матрицы позволяют оценить размеры
и форму облака распределения такой
случайной
величины,
аппроксимировав его эллипсоидом (или
эллипсом в двумерном случае).
23.
Если случайный
вектор
![]() является непрерывным, то его
характеристическая функция (63.1)
определяется через его плотность
является непрерывным, то его
характеристическая функция (63.1)
определяется через его плотность
![]() :
:
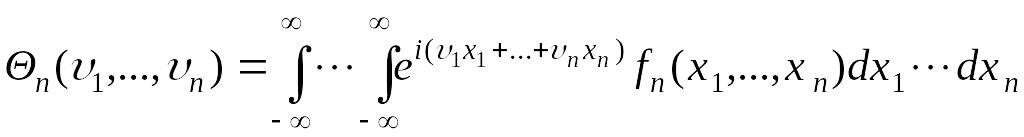 . (63.2)
. (63.2)
Это соотношение
является
![]() - мерным преобразованием Фурье от функции
.
Поэтому плотность
можно выразить через характеристическую
функцию
- мерным преобразованием Фурье от функции
.
Поэтому плотность
можно выразить через характеристическую
функцию
![]() в виде обратного преобразования Фурье
по отношению к (63.2):
в виде обратного преобразования Фурье
по отношению к (63.2):
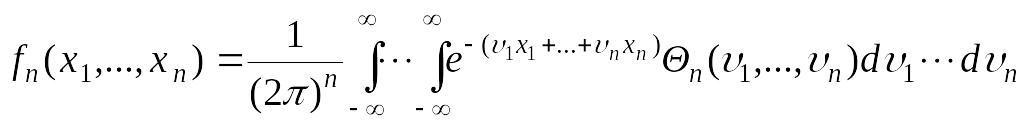 .
(63.3)
.
(63.3)
63.2 Несложно доказать следующие свойства характеристической функции.
1.
![]() .
.
2.
![]() .
.
25.Ковариа́ция — это мера линейной зависимости случайных величин.Св-ва: Ковариация симметрична:
![]() .
.
В силу линейности математического ожидания, ковариация может быть записана как
![]() .
.
Пусть
![]() случайные
величины, а
случайные
величины, а
![]() их
две произвольные линейные
комбинации.
Тогда
их
две произвольные линейные
комбинации.
Тогда
![]() .
.
В частности ковариация (в отличие от коэффициента корреляции) не инварианта относительно смены масштаба, что не всегда удобно в приложениях.
Ковариация случайной величины с собой равна дисперсии:
![]() .
.
Если
![]() независимые
случайные величины, то
независимые
случайные величины, то
![]() .
.
Обратное, вообще говоря, неверно.
Неравенство Коши — Буняковского:
![]()
27.
Определение
5. Пусть дано
семейство случайных величин
![]() ,
так что
,
так что
![]() .
Тогда эти случайные величины попарно
независимы,
если попарно независимы порождённые
ими сигма-алгебры
.
Тогда эти случайные величины попарно
независимы,
если попарно независимы порождённые
ими сигма-алгебры
![]() .
Случайные величины независимы
в совокупности,
если таковы порождённые ими сигма-алгебры.
.
Случайные величины независимы
в совокупности,
если таковы порождённые ими сигма-алгебры.
Определение,
данное выше, эквивалентно любому другому
из нижеперечисленных. Две случайные
величины
![]() независимы
тогда и только тогда, когда:
независимы
тогда и только тогда, когда:
Для любых
![]() :
:
![]()
Для любых борелевских
функций
![]() случайные
величины
случайные
величины
![]() независимы.
независимы.
Для любых ограниченных борелевских функций :
![]()