
- •Основные сведения о матрицах. Операции над матрицами.
- •2.Определитель n-го порядка и их свойства.
- •Определители любого порядка. Свойства определителей.
- •6.Решение системы n линейных уравнений с n неизвестными методом обратных матриц.
- •7. Система m линейных уравнений с n неизвестными. Метод Гаусса.
- •9. Модель Леонтьева многоотраслевой экономики (балансовый анализ).
- •10. Расстояние между двумя точками. Деление отрезка в данном отношении. Площадь треугольника.
- •11. Линии первого порядка на плоскости.
- •12. Параллельность и перпендикулярность прямых.
- •13. Расстояние от точки до прямой.
- •14.Вектор. N-мерное векторное пространство. Линейные операции над векторами.
- •15. Линейная зависимость и независимость векторов. Базис. Разложение вектора по базису.
- •16. Предел функций в точке. Арифметические операций над пределами.
- •Первый замечательный предел
- •Второй замечательный предел
- •18. Бесконечно малые и бесконечно большие функций. Свойства.
- •Свойства бесконечно малых
- •19. Сравнение бесконечно малых.
- •22. Разрывы первого и второго рода.
- •23. Задача о производительности труда. Определение производной. Зависимость между непрерывностью и дифференцируемостью функции.
- •Понятие производной
- •24.Основные правила дифференцирования. Производные элементарных функций. Правила дифференцирования
- •25.Производные обратной и сложной функций.
- •26. Производные и дифференциалы высших порядков.
- •27.Понятие дифференциала функции. Применение дифференциала в приближенных вычислениях.
- •28.Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа.
- •29.Раскрытие неопределенностей.
- •30.Экстремумы функций. Необходимые и достаточные условие экстремума.
- •31.Наибольшее и наименьшее значение функций.
- •32.Выпуклость, вогнутость и точки перегиба кривой.
- •33.Асимптота графика функций. Общая схема исследования и построение графика функций.
- •34.Первообразная функций и неопределенный интеграл. Свойства неопределенного интеграла.
- •41.Дифференциальные уравнения с разделяющимися переменными.
- •42.Однородные линейные дифференциальные уравнения первого порядка.
- •43.Линейные дифференциальные уравнения первого порядка. Использование дифференциальных уравнении в экономике.
- •44. Определение функции двух переменных. Линии и поверхности уровня функции двух переменных.
- •45. Частные производные. Полное производное и полный дифференциал.
- •46. Производная по направлению. Градиент функции.
- •47. Экстремум функции многих переменных (необходимое и достаточное условия).
- •48. Наибольшее и наименьшее значения функции.
- •49. Метод Лагранжа.
- •50. Классическое и статистическое определение вероятности.
- •51. Элементы комбинаторики.
- •52. Теоремы сложения и умножения вероятностей.
- •53. Условная вероятность. Теорема сложения вероятностей для совместных событий.
- •54. Формула полной вероятности. Формула Бейеса.
- •55. Формула Бернулли. Формула Пуассона.
- •56. Понятие случайной величины. Закон распределения дискретных случайных величин.
- •57. Числовые характеристики дискретных случайных величин.
- •58. Биноминальный закон распределения.
- •59. Непрерывная случайная величина. Закон распределения вероятностей и основные числовые характеристики.
- •60. Функция плотности вероятностей.
- •61. Нормальное распределение.
- •62. Неравенство и теорема Чебышева. Закон больших чисел.
- •63. Задача математической статистики. Выборочный метод. Статистические оценки параметров распределения.
- •64. Несмещенные, эффективные и состоятельные оценки.
- •65. Интервальная оценка.
- •66. Корреляционный анализ. Линейная регрессия. Коэффициент корреляции.
15. Линейная зависимость и независимость векторов. Базис. Разложение вектора по базису.
Векторы
![]() называются линейно
зависимыми,
если существует такая линейная комбинация
называются линейно
зависимыми,
если существует такая линейная комбинация
![]() ,
при не равных нулю одновременно
,
при не равных нулю одновременно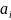 ,
т.е.
,
т.е.
![]() .
Если же только при
= 0 выполняется
,
то векторы называются линейно
независимыми.
.
Если же только при
= 0 выполняется
,
то векторы называются линейно
независимыми.
Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.
Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
Свойство 6. Любые 4 вектора линейно зависимы.
В
частном случае, когда векторы
, . . .,
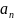 - элементы нек-рого числового поля К,a
k
- подполе в К, возникает понятие линейной
независимости ч и с е л. Л. н. чисел над
полем рациональных чисел Q
можно рассматривать также, как обобщение
понятия иррациональности. Так, числа
a
и 1 линейно независимы тогда и только
тогда, когда a
иррационально.
- элементы нек-рого числового поля К,a
k
- подполе в К, возникает понятие линейной
независимости ч и с е л. Л. н. чисел над
полем рациональных чисел Q
можно рассматривать также, как обобщение
понятия иррациональности. Так, числа
a
и 1 линейно независимы тогда и только
тогда, когда a
иррационально.
Пусть
L, Р и S – прямая, плоскость и пространство
точек соответственно и
![]() .
Тогда
.
Тогда
![]() – векторные пространства векторов как
направленных отрезков на прямой L, на
плоскости Р и в пространстве S
соответственно.
– векторные пространства векторов как
направленных отрезков на прямой L, на
плоскости Р и в пространстве S
соответственно.
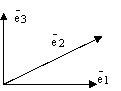
Определение.
Базисом
векторного пространства
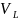 называется любой ненулевой вектор
называется любой ненулевой вектор![]() ,
т.е. любой ненулевой вектор коллинеарный
прямой L:
,
т.е. любой ненулевой вектор коллинеарный
прямой L:
![]() и
и![]() .
.
Обозначение
базиса
:
![]() –
базис
.
–
базис
.
Определение.
Базисом векторного пространства
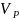 называется любая упорядоченная пара
неколлинеарных векторов пространства
.
называется любая упорядоченная пара
неколлинеарных векторов пространства
.
![]() ,
где
,
где ![]()
![]() ,
,![]() –
базис
–
базис
Определение.
Базисом
векторного пространства называется любая упорядоченная тройка
некомпланарных векторов (т.е. не лежащих
в одной плоскости) пространства
.
называется любая упорядоченная тройка
некомпланарных векторов (т.е. не лежащих
в одной плоскости) пространства
.
![]() –
базис
–
базис
Замечание. Базис векторного пространства не может содержать нулевого вектора: в пространстве по определению, в пространстве два вектора будут коллинеарные, если хотя бы один из них нулевой, в пространстве три вектора будут компланарные, т.е будут лежать в одной плоскости, если хотя бы один из трех векторов будет нулевой.
Разложение вектора по базису.
Определение.
Пусть
![]() –
произвольный вектор,
–
произвольный вектор,
![]() –
произвольная система
векторов. Если выполняется
равенство
–
произвольная система
векторов. Если выполняется
равенство![]() ,то
говорят, что вектор
представлен
в виде линейной комбинации данной
системы
векторов. Если данная система
векторов
является
базисом векторного
пространства, то равенство
называется разложением вектора
по
базису
.
Коэффициенты линейной комбинации
,то
говорят, что вектор
представлен
в виде линейной комбинации данной
системы
векторов. Если данная система
векторов
является
базисом векторного
пространства, то равенство
называется разложением вектора
по
базису
.
Коэффициенты линейной комбинации
![]() называются
в этом случае координатами вектора
относительно
базиса
.
называются
в этом случае координатами вектора
относительно
базиса
.
Теорема. (О разложении вектора по базису.)
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
 Доказательство.
1) Пусть L произвольная прямая (или ось)
и
Доказательство.
1) Пусть L произвольная прямая (или ось)
и
![]() –
базис
–
базис
![]() .
Возьмем произвольный вектор
.
Возьмем произвольный вектор
![]() .
Так как оба вектора
.
Так как оба вектора
![]() и
коллинеарные
одной и той же прямой
L, то
и
коллинеарные
одной и той же прямой
L, то
![]() .
Воспользуемся теоремой о коллинеарности
двух
векторов. Так как
.
Воспользуемся теоремой о коллинеарности
двух
векторов. Так как
![]() ,
то найдется (существует) такое число
,
то найдется (существует) такое число
![]() ,
что
,
что
![]() и
тем самым мы получили разложение вектора
по
базису
векторного
пространства
.
и
тем самым мы получили разложение вектора
по
базису
векторного
пространства
.
Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису векторного пространства :
и
![]() ,
где
,
где
![]() .
Тогда
.
Тогда
![]() и
используя закон дистрибутивности,
получаем:
и
используя закон дистрибутивности,
получаем:
![]() .
.
Так
как
,
то из последнего равенства следует,
что
![]() ,
ч.т.д.
,
ч.т.д.
2)
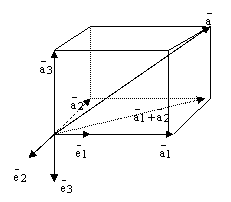
Пусть теперь Р произвольная плоскость
и
![]() –
базис
–
базис
![]() .
Пусть
.
Пусть
![]() произвольный
вектор этой плоскости. Отложим все три
вектора от какой-нибудь одной точки
этой плоскости. Построим 4 прямых.
Проведем прямую
произвольный
вектор этой плоскости. Отложим все три
вектора от какой-нибудь одной точки
этой плоскости. Построим 4 прямых.
Проведем прямую
![]() ,
на которой лежит вектор
,
прямую
,
на которой лежит вектор
,
прямую
![]() ,
на которой лежит вектор
,
на которой лежит вектор
![]() .
Через конец вектора
проведем
прямую
параллельную вектору
и
прямую параллельную вектору
.
Эти 4 прямые
высекают параллелограмм. См. ниже рис.
3. По правилу параллелограмма
.
Через конец вектора
проведем
прямую
параллельную вектору
и
прямую параллельную вектору
.
Эти 4 прямые
высекают параллелограмм. См. ниже рис.
3. По правилу параллелограмма
![]() ,
и
,
и
![]() ,
,
![]() ,
–
базис
,
,
–
базис
,
![]() –
базис
.Теперь,
по уже доказанному в первой
части
этого доказательства, существуют такие
числа
–
базис
.Теперь,
по уже доказанному в первой
части
этого доказательства, существуют такие
числа
![]() ,
что
,
что ![]() и
и
![]() .
Отсюда получаем:
.
Отсюда получаем:
![]() и
возможность разложения по базису
доказана.
и
возможность разложения по базису
доказана.
Теперь докажем
единственность разложения по базису.
Допустим противное. Пусть имеется два
разложения вектора
по
базису
векторного
пространства
:
![]() и
и
![]() .
Получаем равенство
.
Получаем равенство![]() ,
откуда следует
,
откуда следует
![]() .
Если
.
Если
![]() ,
то
,
то
![]() ,
а т.к.
,
а т.к.
![]() ,
то
,
то
![]() и
коэффициенты разложения равны:
и
коэффициенты разложения равны:
![]() ,
,
![]() .
Пусть теперь
.
Пусть теперь
![]() .
Тогда
.
Тогда
![]() ,
где
,
где
![]() .
По теореме о коллинеарности двух
векторов
отсюда следует, что
.
По теореме о коллинеарности двух
векторов
отсюда следует, что
![]() .
Получили противоречие условию теоремы.
Следовательно,
и
,
ч.т.д.
.
Получили противоречие условию теоремы.
Следовательно,
и
,
ч.т.д.
3)
Пусть
![]() –
базис
–
базис
![]() и
пусть
и
пусть
![]() произвольный
вектор. Проведем следующие построения.
произвольный
вектор. Проведем следующие построения.
Отложим
все три базисных вектора
![]() и
вектор
от
одной точки и построим 6 плоскостей:
плоскость, в которой лежат базисные
векторы
и
вектор
от
одной точки и построим 6 плоскостей:
плоскость, в которой лежат базисные
векторы
![]() ,
плоскость
,
плоскость
![]() и
плоскость
и
плоскость
![]() ;
далее через конец вектора
проведем
три плоскости
параллельно только что построенным
трем плоскостям. Эти 6 плоскостей
высекают параллелепипед:
;
далее через конец вектора
проведем
три плоскости
параллельно только что построенным
трем плоскостям. Эти 6 плоскостей
высекают параллелепипед:
По
правилу сложения
векторов
получаем равенство:![]() .
.
По
построению
![]() .
Отсюда, по теореме о коллинеарности
двух
векторов, следует, что существует число
.
Отсюда, по теореме о коллинеарности
двух
векторов, следует, что существует число
![]() ,
такое что
,
такое что
![]() .
Аналогично,
и
.
Аналогично,
и
![]() ,
где
,
где
![]() .
Теперь, подставляя эти равенства в,
получаем
.
Теперь, подставляя эти равенства в,
получаем
![]()
и возможность разложения по базису доказана.
Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису :
и
![]() .
Тогда
.
Тогда![]() .
.
Заметим, что по условию векторы некомпланарные, следовательно, они попарно неколлинеарные.
Возможны два случая: или .
а)
Пусть
,
тогда из равенства следует:
![]() .
.
Из
равенства следует, что вектор
раскладывается
по базису
![]() ,
т.е. вектор
лежит
в плоскости
векторов
и,
следовательно, векторы
компланарные,
что противоречит условию.
,
т.е. вектор
лежит
в плоскости
векторов
и,
следовательно, векторы
компланарные,
что противоречит условию.
б)
Остается случай
,
т.е.
![]() .
Тогда из равенства получаем
.
Тогда из равенства получаем
![]() или
или
![]() . Так
как
–
базис
пространства
векторов
лежащих в плоскости, а мы уже доказали
единственность разложения по базису
векторов
плоскости, то из равенства (5) следует,
что
и
. Так
как
–
базис
пространства
векторов
лежащих в плоскости, а мы уже доказали
единственность разложения по базису
векторов
плоскости, то из равенства (5) следует,
что
и
![]() ,
ч.т.д.
,
ч.т.д.
