
- •Основные сведения о матрицах. Операции над матрицами.
- •2.Определитель n-го порядка и их свойства.
- •Определители любого порядка. Свойства определителей.
- •6.Решение системы n линейных уравнений с n неизвестными методом обратных матриц.
- •7. Система m линейных уравнений с n неизвестными. Метод Гаусса.
- •9. Модель Леонтьева многоотраслевой экономики (балансовый анализ).
- •10. Расстояние между двумя точками. Деление отрезка в данном отношении. Площадь треугольника.
- •11. Линии первого порядка на плоскости.
- •12. Параллельность и перпендикулярность прямых.
- •13. Расстояние от точки до прямой.
- •14.Вектор. N-мерное векторное пространство. Линейные операции над векторами.
- •15. Линейная зависимость и независимость векторов. Базис. Разложение вектора по базису.
- •16. Предел функций в точке. Арифметические операций над пределами.
- •Первый замечательный предел
- •Второй замечательный предел
- •18. Бесконечно малые и бесконечно большие функций. Свойства.
- •Свойства бесконечно малых
- •19. Сравнение бесконечно малых.
- •22. Разрывы первого и второго рода.
- •23. Задача о производительности труда. Определение производной. Зависимость между непрерывностью и дифференцируемостью функции.
- •Понятие производной
- •24.Основные правила дифференцирования. Производные элементарных функций. Правила дифференцирования
- •25.Производные обратной и сложной функций.
- •26. Производные и дифференциалы высших порядков.
- •27.Понятие дифференциала функции. Применение дифференциала в приближенных вычислениях.
- •28.Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа.
- •29.Раскрытие неопределенностей.
- •30.Экстремумы функций. Необходимые и достаточные условие экстремума.
- •31.Наибольшее и наименьшее значение функций.
- •32.Выпуклость, вогнутость и точки перегиба кривой.
- •33.Асимптота графика функций. Общая схема исследования и построение графика функций.
- •34.Первообразная функций и неопределенный интеграл. Свойства неопределенного интеграла.
- •41.Дифференциальные уравнения с разделяющимися переменными.
- •42.Однородные линейные дифференциальные уравнения первого порядка.
- •43.Линейные дифференциальные уравнения первого порядка. Использование дифференциальных уравнении в экономике.
- •44. Определение функции двух переменных. Линии и поверхности уровня функции двух переменных.
- •45. Частные производные. Полное производное и полный дифференциал.
- •46. Производная по направлению. Градиент функции.
- •47. Экстремум функции многих переменных (необходимое и достаточное условия).
- •48. Наибольшее и наименьшее значения функции.
- •49. Метод Лагранжа.
- •50. Классическое и статистическое определение вероятности.
- •51. Элементы комбинаторики.
- •52. Теоремы сложения и умножения вероятностей.
- •53. Условная вероятность. Теорема сложения вероятностей для совместных событий.
- •54. Формула полной вероятности. Формула Бейеса.
- •55. Формула Бернулли. Формула Пуассона.
- •56. Понятие случайной величины. Закон распределения дискретных случайных величин.
- •57. Числовые характеристики дискретных случайных величин.
- •58. Биноминальный закон распределения.
- •59. Непрерывная случайная величина. Закон распределения вероятностей и основные числовые характеристики.
- •60. Функция плотности вероятностей.
- •61. Нормальное распределение.
- •62. Неравенство и теорема Чебышева. Закон больших чисел.
- •63. Задача математической статистики. Выборочный метод. Статистические оценки параметров распределения.
- •64. Несмещенные, эффективные и состоятельные оценки.
- •65. Интервальная оценка.
- •66. Корреляционный анализ. Линейная регрессия. Коэффициент корреляции.
14.Вектор. N-мерное векторное пространство. Линейные операции над векторами.
Вектором называется направленный отрезок. Если начало вектора находится в точке А, а конец – в точке В, то вектор обозначается АВ. Если же начало и конец вектора не указываются, то его обозначают строчной буквой латинского алфавита a, b, c ,…. Через BA обозначают вектор, направленный противоположно вектору АВ. Вектор, у которого начало и конец совпадают, называется нулевым и обозначается ō. Его направление является неопределенным.
Алгебраический подход
В линейной алгебре вектор — это элемент векторного пространства (или иначе: линейного пространства). Векторы можно складывать и умножать на число. Вектор также можно представить в виде линейной комбинации других векторов. Базис — это линейно независимая совокупность векторов, которая порождает всё пространство. В конечномерном пространстве существует конечный базис, и тогда любой вектор пространства может быть единственным образом представлен в виде разложения вида
![]() где
—
где
—
![]() это базис, а —
это базис, а —
![]() координаты вектора
координаты вектора
![]() в заданном базисе.
в заданном базисе.
Геометрический подход
Понятие вектор в геометрии отлично от определяемого в алгебре. Различают понятие свободного и связанного (приложенного, закреплённого) вектора.
Связанный вектор или направленный отрезок — упорядоченная пара точек евклидова пространства.
Свободный вектор — класс эквивалентности направленных отрезков.
При этом два направленных отрезка считаются эквивалентными, если они:
коллинеарны
равны по длине
одинаково направлены (сонаправлены)
Векторное
пространство
Векторное пространство называют.
n-мерным (или имеет «размерность n»),
если в нём существуют n линейно независимых
элементов
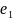 ,
,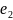 ,
...
,
...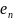 ,
а любые n+1 элементов линейно зависимы.
Векторное пространство называют
бесконечномерным, если в нём для любого
натурального n существует n линейно
независимых векторов. Любые n линейно
независимых векторов n-мерного векторного
пространства образуют базис этого
пространства. Если
,
,
...
- базис векторного пространства, то
любой вектор x этого пространства может
быть представлен единственным образом
в виде линейной комбинации базисных
векторов:
,
а любые n+1 элементов линейно зависимы.
Векторное пространство называют
бесконечномерным, если в нём для любого
натурального n существует n линейно
независимых векторов. Любые n линейно
независимых векторов n-мерного векторного
пространства образуют базис этого
пространства. Если
,
,
...
- базис векторного пространства, то
любой вектор x этого пространства может
быть представлен единственным образом
в виде линейной комбинации базисных
векторов:
x
=
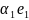 +
+
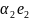 + ... +
+ ... +
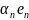 .
.
При
этом числа
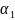 ,
,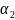 ,
...,
,
...,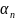 называют координатами вектора x в данном
базисе.
называют координатами вектора x в данном
базисе.
Линейными операциями над векторами называется сложение и умножение на число.
умножение вектора на число (Произведением вектора a и числа α называется вектор, обозначаемый α∙a. (или наоборот a∙α), модуль которого равен |α a| =|α||a|, а направление совпадает с направлением вектора a, если α>0, и противоположно ему, если α< 0.
Из определения произведения вектора на число легко вывести следующие свойства:
если
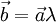 ,
то
,
то
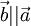 .
Наоборот, если
.
Наоборот, если
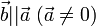 ,
то при некотором λ верно равенство
;
,
то при некотором λ верно равенство
;всегда
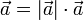 °,
то есть каждый вектор равен произведению
его модуля на
°,
то есть каждый вектор равен произведению
его модуля на
cуммой
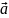 +
+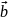 двух векторов
и
называется вектор
двух векторов
и
называется вектор
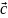 ,
который идет из начала вектора
в конец вектора
при условии, что вектор
приложен к концу вектора
(правило треугольника). В случае
неколлинеарных векторов
и
можно вместо правила треугольника
использовать правило параллелограмма:
если векторы
и
отложены от общего начала и на них
построен параллелограмм, то сумма
+
есть вектор, совпадающий с диагональю
этого параллелограмма, идущего из
общего начала
и
.
,
который идет из начала вектора
в конец вектора
при условии, что вектор
приложен к концу вектора
(правило треугольника). В случае
неколлинеарных векторов
и
можно вместо правила треугольника
использовать правило параллелограмма:
если векторы
и
отложены от общего начала и на них
построен параллелограмм, то сумма
+
есть вектор, совпадающий с диагональю
этого параллелограмма, идущего из
общего начала
и
.
