66. Корреляционный анализ. Линейная регрессия. Коэффициент корреляции.

Корреляционный анализ — метод обработки статистических данных, заключающийся в изучении коэффициентов корреляции между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков для установления между ними статистических взаимосвязей. Цель корреляционного анализа — обеспечить получение некоторой информации об одной переменной с помощью другой переменной. В случаях, когда возможно достижение цели, говорят, что переменные коррелируют. В самом общем виде принятие гипотезы о наличии корреляции означает что изменение значения переменной А, произойдет одновременно с пропорциональным изменением значения Б. Корреляция отражает лишь линейную зависимость величин, но не отражает их функциональной связности. Например, если вычислить коэффициент корреляции между величинами A = sin(x) и B = cos(x), то он будет близок к нулю, то есть (линейная) зависимость между величинами отсутствует. Между тем, величины A и B очевидно связаны функционально по закону sin2(x) + cos2(x) = 1. Линейная Регрессия. Некая фирма решила использовать модель линейной регрессии для определения зависимости вида y = a + bx между годовым объемом продаж и годовыми расходами на рекламу. За предшествующие годы были собраны следующие данные:

Объем продаж (млн. $) (yi)	Расходы на рекламу (тыс. $) (xi)
28	71
14	31
19	50
21	60
16	35

1. Найдем линейную теоретическую функцию регрессии y = a + bx и параметры линейной регрессии (коэффициенты регрессии) a и b, используя метод наименьших квадратов. Для этого надо решить следующую систему уравнений: В нашем случае n=5 - число наблюдений и:

Подставив эти значения в вышеуказанные уравнения: 98 = 5a + 247b 5192 = 247a + 13327b

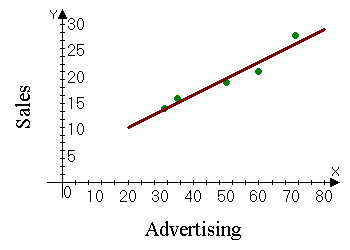
Решив эту систему относительно a и b, получим a=4,2 и b=0,31. Таким образом, ожидаемые продажи будут составлять 4.2 плюс 0.31 умножить на рекламный бюджет, y = 4,2 + 0,31x То есть, если расходы на рекламу на следующий год составят $40 000, то можно ожидать, что продажи составят $16 600 000. На графике наблюдения и функция регрессии выглядят следующим образом: a называется постоянным коэффициентом линейной регрессии, а b переменным коэффициентом линейной регрессии.

Итого, в Части 1 из статистических данных мы получили: теоретическую функцию регрессии, постоянный и переменный коэффициенты регрессии.

В Части 2 мы получим: средние квадратические отклонения ошибок коэффициентов регрессии, коэффициент детерминации r2, доверительные интервалы для оценки значимости параметров модели. Коэффициент корреляции. Как мы знаем, если и - независимые случайные величины, то по свойству математического ожидания (72) Если же и не являются независимыми случайными величинами, то, вообще говоря, . Условились за меру связи (зависимости) двух случайных величин и принять безразмерную величину соотношением. (73) и называемую коэффициентом корреляции. Рассмотрим некоторые свойства коэффициента корреляции.

Если и - независимые случайные величины, то коэффициент корреляции равен нулю. Это свойство непосредственно вытекает из соотношений (72) и (73). Заметим, что обратное утверждение, вообще говоря, неверно, т. е. если , то отсюда еще не следует, что и независимы.