43.Линейные дифференциальные уравнения первого порядка. Использование дифференциальных уравнении в экономике.

ОПРЕДЕЛЕНИЕ. Уравнение вида:

y'+p(x)у=q(х) (10)

где р(х) и q(х) — непрерывные функции, называется линейным дифференциальным уравнением первого порядка. Название уравнения объясняется тем, что неизвестная функция у и ее производная у' входят в уравнение линейно, т. е. в первой степени.

ОПРЕДЕЛЕНИЕ. Если q(х) = 0, то уравнение (10) называется линейным однородным уравнением. Если q(х)≠0, то уравнение (10) называется линейным неоднородным уравнением.

Для нахождения общего решения уравнения (10) может быть применен метод вариации постоянной. В этом методе сначала находят общее решение линейного однородного уравнения:

у'+р(х)у=0 (11)

соответствующего данному неоднородному уравнению (10). Уравнение (11) является уравнением с разделяющимися переменными. Разделяя переменные и интегрируя, имеем:

=-p(x)dx ⇒ ln|y|=-∫p(x)dx+ln|C1|

Отсюда, потенцируя, находим общее решение данного уравнения:

y=±C1e-∫p(x)dx, или y=Ce-∫p(x)dx (12)

где С=±C1 — произвольная постоянная.

Теперь найдем общее решение уравнения (10) в виде (12), где С будем считать не постоянной, а новой неизвестной функцией от х (в этом смысл метода!), т. е. в виде

y=C(x)e-∫p(x)dx (13)

Чтобы найти функцию С(х) подставим решение в виде (13) в уравнение (10). Получим:

C'(x)e-∫p(x)dx-C(x)p(x)e-∫p(x)dx+p(x)C(x)e-∫p(x)dx=q(x) (14)

или

C'(x)=q(x)e∫p(x)dx (14')

Итак, чтобы функция (13) являлась решением уравнения (10), функция С(х) должна удовлетворять уравнению (14). Интегрируя его, находим:

C(x)=q(x)e∫p(x)dxdx+C1

где C1 — произвольная постоянная. Подставляя найденное выражение для С (х) в соотношение (10), получаем общее решение линейного уравнения (10):

y(x)=C1e-∫p(x)dx+e-∫p(x)dx∫q(x)e∫p(x)dxdx

Пример 7. Найти общее решение уравнения у'+Зу=е2х.

Данное уравнение является линейным. Здесь р(х)=3, q(х)=е2х. Решаем сначала соответствующее однородное уравнение y'+3y=0. Разделяя переменные =-3dx и интегрируя, находим ln|y|=-3x+ln|C1| или y=±C1e-3x=Ce-3x. Ищем общее решение данного уравнения в виде y=C(x)e-3x. Дифференцируя, имеем y'=C'(x)e-3x-3C(x)e-3x. Подставляя в данное уравнение выражения для у и у', получаем C'(x)e-3x=e2x, C'(x)=e5x или dC=e5xdx, откуда C(x)=e5x+C2, где C2 - произвольная постоянная. Следовательно, общее решение данного уравнения имеет вид:

y=C(x)e-3x=(e5x+C2)e-3x или y=e2x+C2e-3x

44. Определение функции двух переменных. Линии и поверхности уровня функции двух переменных.

45. Частные производные. Полное производное и полный дифференциал.

46. Производная по направлению. Градиент функции.

 Пусть  -- внутренняя точка области , и в области задана функция . Рассмотрим ограничение функции на прямую , проходящую через точку параллельно оси . Эта прямая задаётся условиями при ; переменная может при этом произвольно меняться. Поэтому для рассматриваемого ограничения имеется естественная параметризация, смысл которой в том, что "замораживаются" все переменные, от которых зависит , кроме :

 

Получили функцию одного переменного , как параметризацию ограничения с помощью параметра .

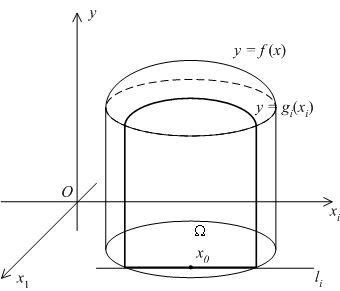
Рис.7.12.

Функция может иметь производную в точке , равную некоторому числу . Это число называют частной производной функции по переменной , вычисленной в точке . Эта частная производная обозначается 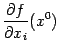или .

Сразу же заметим, что значения частных производных от функции в точке , вычисленные по разным переменным и , могут быть различными, так что обозначение типа , без указания переменной, по которой вычислена частная производная, не имеет смысла: в обозначении обязательно нужно указывать переменную, по которой мы дифференцируем.

Итак, чтобы вычислить частную производную от функции по некоторой переменной , нужно фиксировать значения всех переменных, кроме (то есть временно считать их постоянными), а затем по обычным правилам вычисления производных найти производную по этой единственной переменной . Теперь ясно, что для вычисления частных производных никаких новых правил дифференцирования вдобавок к тем, что известны нам для функций одной переменной, не потребуется, ведь при вычислении частной производной мы считаем, что может изменяться только одна переменная. Считая точку , в которой вычисляется значение частной производной , переменной точкой области и предполагая, что во всех точках эта производная существует, мы получаем, что частная производная  -- это функция, заданная в области (или в её части, если производная существует не везде в ). Производные и дифференциалы функций нескольких переменных.Определение. Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение х к переменной х. Тогда величина _xz = f( x + x, y) – f(x, y) называется частным приращением функции по х.

Можно записать

Тогда  называется частной производной функции z = f(x, y) по х.

Обозначение: Аналогично определяется частная производная функции по у.   Геометрическим смыслом частной производной (допустим ) является тангенс угла наклона касательной, проведенной в точке N₀(x₀, y₀, z₀) к сечению поверхности плоскостью у = у₀.

Полное приращение и полный дифференциал.

  Определение. Для функции f(x, y) выражение z = f( x + x, y + y) – f(x, y) называется полным приращением.

Если функция f(x, y) имеет непрерывные частные производные, то

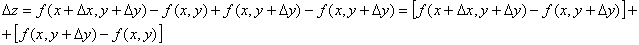 Применим теорему Лагранжа к выражениям, стоящим в квадратных скобках. здесь

Тогда получаем Т.к. частные производные непрерывны, то можно записать равенства:  

  Определение. Выражение называется полным приращением функции f(x, y) в некоторой точке (х, у), где ₁ и ₂ – бесконечно малые функции при х  0 и у  0 соответственно.

  Определение: Полным дифференциалом функции z = f(x, y) называется главная линейная относительно х и у приращения функции z в точке (х, у).

  Для функции произвольного числа переменных:

Пример. Найти полный дифференциал функции