
vostrikov
.pdf
4.3. Критерии устойчивости |
101 |
Так как положительность всех коэффициентов характеристического уравнения следует из необходимого условия, то условие устойчивости системы третьего порядка принимает вид
a3a2 a1.
Данное соотношение можно рассматривать как частный случай критерия Гурвица, т. е. оно является необходимым и достаточным условием устойчивости для систем третьего порядка.
ПРИМЕР 4.4
Проверить с помощью критерия Гурвица устойчивость двигателя постоянного тока с независимым возбуждением, полагая в качестве выходной переменной угол поворота двигателя , который связан с угловой
скоростью вращения соотношением
d dt .
Добавим к основным уравнениям двигателя, приведенным в примере 2.4, выражение для угловой скорости вращения и получим модель объекта
L |
|
dI |
|
RI |
c |
|
U |
|
, |
|
|
|
я |
||||||
|
|
dt |
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
||
J |
d |
c I |
M |
|
, |
|
|
||
|
c |
|
|
||||||
|
|
dt |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
d dt .
Запишем ее в виде одного дифференциального уравнения относительно переменной :
TяTм |
Tм |
ku kм (Tя p 1)M , |
все параметры которого приведены в примере 2.4. Определим передаточную функцию двигателя по управлению, полагая М = 0,
W ( p) |
|
|
k |
|
. |
|
|
|
|
||
u |
TяTм p3 Tм p2 |
|
|||
|
p |
||||
Характеристическое уравнение имеет вид
T T p3 |
T p2 |
p 0. |
я м |
м |
|

102 |
|
|
|
Глава 4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ |
|||||||
|
Предварительно запишем это уравнение в стандартной форме |
||||||||||
|
|||||||||||
|
|
p3 |
1 |
|
p2 |
1 |
|
p 0 |
|||
|
|
|
|
|
|
|
|||||
|
|
|
Tя |
TяTм |
|
|
|||||
|
и составим матрицу Гурвица |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Tя |
|
||||||
|
|
|
|
|
|
|
|
|
|||
|
|
H |
1 |
|
1 |
|
0 |
. |
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
TяTм |
|
||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
0 |
|
0 |
|
|||
|
Как видим, det H |
0. Следовательно, двигатель постоянного тока с не- |
|||||||||
|
зависимым возбуждением, выходной переменной которого является угол |
||||||||||
|
поворота, находится на границе устойчивости. |
||||||||||
4.3.2. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
Критерий сформулирован А.В. Михайловым в 1938 г., он базируется на принципе аргумента теории функций комплексной переменной.
Для анализа устойчивости системы предлагается исследовать характеристический комплекс F ( j ) , который получается из
характеристического полинома
F( p) |
pn |
a pn 1 |
a p |
a |
(4.16) |
|
|
n |
2 |
1 |
|
заменой p на j : |
|
|
|
|
|
F( j ) |
( j |
)n a ( j |
)n 1 a . |
(4.17) |
|
|
|
n |
|
1 |
|
Выделим в (4.17) вещественную и мнимую части, а также модуль и фазу:
F( j ) RF ( ) jIF ( ) AF ( )e |
j |
F ( |
) |
. |
(4.18) |
|
|
|
|||
При конкретном численном значении частоты ( |
|
1 ) |
характери- |
||
стический комплекс (4.18) представляет собой комплексное число

4.3. Критерии устойчивости |
|
|
|
|
|
|
|
|
|
|
103 |
||||
|
|
|
|
|
|
Im |
|
|
|
|
|
|
|
|
|
F |
j 1 , |
которое можно изобразить |
|
|
Im |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
на |
плоскости в |
виде |
вектора, |
соеди- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
AА((jj ) |
) |
|
Re |
|
|||||||
няющего |
начало |
координат с |
точкой |
|
|
|
|
a |
|
||||||
|
|
|
|
|
|
|
Re |
||||||||
|
|
|
|
|
|
|
|||||||||
RF ( 1); jIF ( 1) . |
|
|
|
|
|
|
|
|
|
а11 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
При изменении |
от 0 до |
конец |
|
|
|
|
|
|
|
|
|
|
||
вектора F j выписывает на ком-
плексной плоскости некоторую кривую, которую называют годографом
Михайлова (рис. 4.8). Причем начинается годограф, как следует из соотношения (4.17), в точке с координатами a1; j0 .
Формулировка критерия. Для устойчивости линейной системы необходимо и достаточно, чтобы годограф Михайлова при изменении от 0 до начинался на вещественной оси в точке a1 и проходил
последовательно против часовой стрелки n квадрантов комплексной плоскости, не обращаясь в нуль и стремясь к в n-м квадранте.
Чтобы доказать критерий, проанализируем, как связаны корни ха-
рактеристического уравнения |
i |
с видом годографа Михайлова. По- |
|
|
скольку полином (4.16) можно представить в виде произведения простых сомножителей
F( p) |
( p 1) ( p |
n ), |
(4.19) |
|||
характеристический комплекс (4.17) также принимает вид |
|
|||||
F( j |
) |
( j |
1) ( j |
n ). |
(4.20) |
|
Его можно представить в форме |
|
|
|
|||
F( j ) |
A ( |
)e j 1( |
) A ( )e j n ( ). |
(4.21) |
||
|
1 |
|
|
n |
|
|
Из выражений (4.18) и (4.21) следует, что |
|
|||||
|
|
|
n |
|
|
|
|
AF ( |
) |
Ai ( |
), |
(4.22) |
|
|
|
|
i |
1 |
|
|
|
|
|
n |
|
|
|
|
F ( |
) |
i ( |
). |
(4.23) |
|
|
|
|
i |
1 |
|
|

104 Глава 4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
Если характеристическое уравнение системы содержит комплексносопряженные корни с нулевой вещественной частью, то при опреде-
ленном значении частоты |
0 |
один из сомножителей в (4.20) обра- |
|
|
|
тится в нуль. Следовательно, |
AF ( ) 0 и F ( j ) 0. В случае устой- |
|
чивой системы корни расположены только в левой полуплоскости плоскости корней и не могут быть «мнимыми», значит, в нуль годограф Михайлова не обращается.
Определим теперь угол поворота вектора F ( j ) при изменении
частоты от 0 до . Предварительно рассмотрим отдельные сомножители выражения (4.20) и угол поворота соответствующего вектора. При этом выделим несколько вариантов корней.
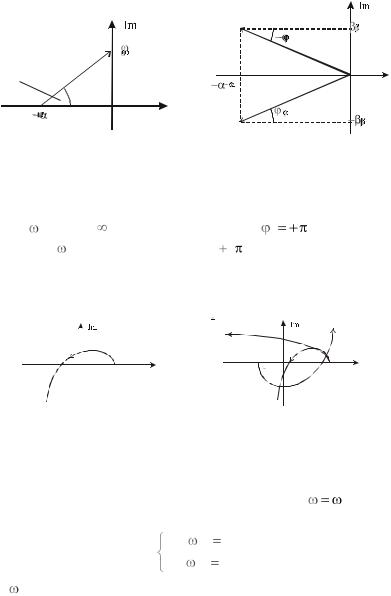
1. Корень характеристического уравнения вещественный и отрица-
тельный, т. е. |
i |
|
i , |
i 0. |
Соответствующий сомножитель в |
||
(4.20) имеет вид |
Fi |
j |
j |
i . |
Изобразим этот элементарный век- |
||
тор на комплексной плоскости; при изменении |
от 0 до |
вещест- |
|||||
венная часть Fi |
j |
остается неизменной и равной |
i , а мнимая часть |
||||
возрастает до бесконечности (рис. 4.9). |
|
|
|||||
Следовательно, устойчивому вещественному корню соответствует
угол поворота элементарного вектора |
i |
2. |
|
|
Аналогично можно определить угол поворота элементарного векто-
ра Fi ( j ) j |
i для случая вещественного положительного корня |
||
характеристического уравнения i |
i. Он будет равен i |
2. |
|
2. Рассмотрим теперь пару устойчивых комплексно-cопряженных
корней |
i,i 1 |
i |
j i и соответствующий им угол поворота произве- |
дения |
i |
j i j |
i j i j . |
У этих двух векторов начальные фазы одинаковы по модулю ( 0 ),
но имеют противоположные знаки. При изменении |
от 0 до |
один |
|||||
вектор |
поворачивается на угол |
i |
0 |
2, а |
второй – на |
угол |
|
|
|
|
|
|
|
||
i 1 |
0 |
2. |
|
|
|
|
|
|
|
|
|
|
|
||
Суммарный угол поворота для пары устойчивых комплексно-
сопряженных корней равен |
(рис. 4.10). |
Если комплексно-сопряженные корни имеют положительную вещественную часть, то суммарный угол поворота равен .
4.3. Критерии устойчивости |
|
|
|
|
|
|
|
|
105 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im |
Im |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im |
|
|
Im |
|
|
|
|
|
|
|
|
|
|
|
|
|
i i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
jj |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Фазаф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
i i |
|
|
|
|
|
|
|
|
|
|
|
|
Re |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i i |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Рис. 4.9. Элементарный вектор, |
Рис. 4.10. Векторы, соответству- |
|||||||||||||||||||||||||||
соответствующий устойчивому |
ющие |
устойчивым комплексно- |
||||||||||||||||||||||||||
|
вещественному корню |
|
|
|
сопряженным корням |
|||||||||||||||||||||||
Таким образом, в устойчивой системе каждый из n корней при из-
менении от 0 до даст приращение фазы |
i |
|
 2, а общий угол
2, а общий угол
поворота F j согласно (4.23) равен  2 n, что и требовалось до-
2 n, что и требовалось до-
казать.
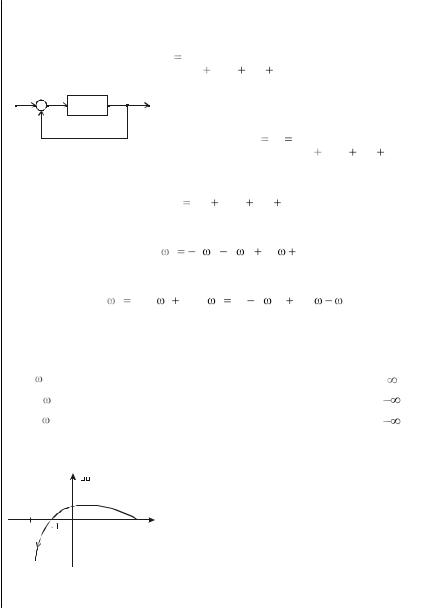
Пример годографов Михайлова для устойчивых и неустойчивых систем третьего порядка приведен на рис. 4.11.
3 |
Im |
|
|
|
|
|
|
n |
3 |
|
Im |
|
Im |
|
|
|
|
|
|
|
Im |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
|
|
|
|
|
|
Re |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
а1a1 |
Re |
|
|
|
|
–1а1 |
|
|
|
|
а11 |
|
Re |
||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
система устойч |
|
|
|
|
|
|
|
система неу |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
а |
|
|
б |
|
|
|
|
|
|
|
||||||||
|
Рис. 4.11. Годографы Михайлова для устойчивой (а) |
|
|
|||||||||||||||||
|
|
и неустойчивой (б) систем (n = 3) |
|
|
|
|
|
|
|
|||||||||||
Условием границы устойчивости является обращение в нуль годо-
графа Михайлова при некотором значении частоты |
0. Аналити- |
|||
чески это условие можно записать в виде |
|
|||
RF ( |
0 ) |
0, |
(4.24) |
|
IF ( |
0 ) |
0. |
||
|
||||
Здесь 0 – частота незатухающих колебаний, возникающих в системе, которая находится на границе устойчивости.
106 |
Глава 4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ |
ПРИМЕР 4.5
Проверить устойчивость системы (рис. 4.12). Здесь
W0 ( p)
v |
|
|
W ( p) |
y |
|
|
|
|
|
|
|
|
W0o(p) |
|
Рис. 4.12. Структурная схема исследуемой системы
|
2 |
|
. |
|
|
|
|
p3 |
2 p2 |
|
|
2 p 1 |
|||
Определим передаточную функцию замкнутой системы
W ( p) |
y |
2 |
|
|
|
|
|
u |
|
p3 2 p2 2 p 3 |
|
|
|
||
и запишем ее характеристический полином
F ( p) p3 2 p2 2 p 3.
Перейдем к выражению для годографа Михайлова
F ( j ) |
j 3 2 2 2 j |
3 |
и представим его в форме
F ( j ) R ( ) jI |
F |
( ) (3 2 2 ) j(2 |
3 ). |
F |
|
|
Для построения годографа Михайлова вычислим значения вещественной и мнимой частей при конкретных значениях частоты и занесем их в таблицу.
|
|
0 |
1 |
1,22 |
1,41 |
|
|
|
|
|
|
|
|
|
|
RF ( |
) |
3 |
1 |
0 |
–1 |
|
|
IF ( |
) |
0 |
1 |
0,61 |
0 |
|
|
По данным таблицы построим годограф Михайлова.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как видим из рис. 4.13, он проходит |
Im |
|
|
Im |
|
|
|
|
последовательно три квадранта, не обра- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щаясь в нуль и стремясь к бесконечности в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
|
третьем квадранте. Следовательно, систе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ма устойчива. |
1 |
|
|
3 |
|
|
|||||||||||
–1 |
|
|
|
|
|
|
|
|
|
|
Re |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.13. Годограф Михайлова для примера 4.5

4.3. Критерии устойчивости |
107 |
ПРИМЕР 4.6
Проверить устойчивость системы (рис. 4.14). Данная система представляет собой упрощенную модель одного из сочленений руки роботаманипулятора [43]. Исполнительным механизмом является двигатель постоянного тока (см. пример 2.4), а соединение с рукой осуществляется через редуктор. На рис. 4.14 обозначено:
Uя – напряжение, подаваемое на якорь двигателя;
– угловая скорость вращения двигателя;
1 |
– угол поворота вала двигателя; |
|
|
|
||||||
2 |
– угол поворота руки. При отсутствии возмущений взаимосвязь |
|||||||||
между скоростью вращения двигателя |
|
и входным напряжением Uя оп- |
||||||||
ределяет передаточная функция (см. пример 2.8) |
||||||||||
|
|
Wдв ( p) |
|
|
|
k |
|
, |
||
|
|
|
|
|
|
|
||||
|
|
T T |
|
p2 |
|
|
||||
|
|
|
|
|
|
|
T p 1 |
|||
|
|
|
|
|
я м |
|
|
м |
||
а угол поворота вала двигателя |
1 |
связан с его угловой скоростью враще- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
ния зависимостью |
|
1 |
. Ей соответствует на схеме вторая передаточная |
|||||||
|
|
|
|
|
|
|
|
|
|
|
функция 1 p . Редуктор представляет собой безынерционное звено с пере-
p . Редуктор представляет собой безынерционное звено с пере-
даточной функцией Wр ( p) 1r , где r – передаточное отношение редуктора.
Uя |
|
|
|
1 |
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
Uя |
Wдв((p) |
|
|
Wp((pp)) |
|
|||||
|
|
|
|
|
|
|
||||
|
дв |
p |
|
|
|
р |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Двигательдвигатель |
|
|
|
|
Редукторредуктор |
|
||
Рис. 4.14. Структурная схема руки робота
Проверим устойчивость системы при следующих значениях парамет-
ров передаточных функций: |
W |
|
( p) |
|
0, 6 |
|
, |
W ( p) |
1 |
. |
||||
|
|
|
дв |
|
|
|
0,13 p2 |
1, 43 p |
1 |
р |
30 |
|
||
|
|
|
|
|
|
|
|
|
|
|||||
Определим общую передаточную функцию сочленения руки робота |
|
|
||||||||||||
W ( p) |
|
k r |
|
|
|
|
|
|
0, 02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T T p2 |
T |
p |
1 p 0,13p2 |
1, 43p |
1 p |
|
|
|
||||||
|
|
|
|
|||||||||||
|
я м |
м |
|
|
|
|
|
|
|
|
|
|
|
|

108 |
|
Глава 4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ |
||||
и запишем характеристический полином |
|
|
|
|||
|
F ( p) |
0,13 p2 |
1, 43 p |
1 |
p. |
|
Выражение для годографа Михайлова |
|
|
|
|||
F |
j |
j 0,13 |
3 |
1, 43 |
2 |
j |
представим в форме |
|
|
|
|
|
|
F |
j |
1, 43 2 |
j |
0,13 |
3 . |
|
Поскольку при |
0 вещественная и мнимая части F ( j ) одновре- |
|||||
менно обращаются в нуль, годограф Михайлова начинается в начале координат. Это означает, что система находится на границе устойчивости.
4.3.3. КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА
На практике более широкое применение по сравнению с критерием Михайлова получил критерий Н. Найквиста, который был разработан в 1932 г. для проверки устойчивости усилителей с отрицательной обратной связью, а затем обобщен на системы автоматического управления. Возможно, именно этот результат послужил толчком к бурному развитию частотного метода в теории автоматического управления.
Критерий Найквиста позволяет определить устойчивость системы с отрицательной обратной связью (так называемой замкнутой системы) по экспериментально снятой или полученной на основе передаточной функции амплитудно-фазовой частотной характеристики разомкнутой системы.
|
|
|
|
|
Рассмотрим этот критерий для сис- |
vv |
|
Wo0(p) |
y y |
||
|
|
|
|
темы с единичной обратной связью |
|
|
|
|
|
||
|
|
|
|
(рис. 4.15). Здесь W0 ( p) – передаточная функция устойчивой разомкнутой сис-
темы, которая в общем случае имеет вид
Рис. 4.15. Структурная схема замкнутой системы
W0 ( p)
где A |
0 |
( p) |
pn a pn 1 |
a – ее характеристический полином. |
|
|
n |
1 |
B0 ( p)
A0 ( p)

4.3. Критерии устойчивости |
109 |
Определим передаточную функцию системы, изображенной на рис. 4.15:
W ( p) |
|
B( p) |
|
|
W0 ( p) |
|
|
B0 ( p) |
|
, |
(4.26) |
|||
|
A( p) 1 |
W0 ( p) A0 ( p) |
B0 ( p) |
|||||||||||
где A( p) A0 ( p) B0 ( p) – характеристический полином |
замкнутой |
|||||||||||||
системы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предварительно введем вспомогательную передаточную функцию |
||||||||||||||
|
|
|
|
|
|
A0 ( p) B0 ( p) |
|
A( p) |
|
(4.27) |
||||
W ( p) |
1 W0 ( p) |
|
|
A0 ( p) |
A0 ( p) |
. |
||||||||
|
|
|
|
|
|
|
|
|
||||||
Как видим, ее числитель представляет собой характеристический полином замкнутой системы, а знаменатель – характеристический по-
лином разомкнутой системы. Так как deg B0 ( p) |
deg A0 ( p), |
в выражении |
для A( p) порядок суммы полиномов равен |
deg A0 ( p) |
n. Следова- |
тельно, во вспомогательной передаточной функции W ( p) полиномы
числителя и знаменателя имеют одинаковый порядок, равный n. Получим выражение для вспомогательной частотной характеристи-
ки на основе выражения (4.27):
|
A( j |
) |
|
|
W ( j ) |
A0 ( j |
) |
. |
(4.28) |
|
|
|
|
|
Рассмотрим теперь результирующий угол поворота вектора W j |
||||
при изменении от 0 до , используя те же соотношения, что и при
доказательстве критерия Михайлова. Если замкнутая система устойчивая, то общее приращение фазы числителя (4.28) будет
( ) n( / 2). |
(4.29) |
При устойчивой разомкнутой системе фаза знаменателя определя-
ется соотношением |
|
|
|
|
0 ( |
) |
n( / 2). |
|
(4.30) |
Результирующий угол поворота вектора |
|
) будет равен разно- |
||
W ( j |
||||
сти фаз (4.29) и (4.30), т. е. |
|
|
|
|
( ) |
( ) |
0 ( ) |
0. |
(4.31) |

110 |
Глава 4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ |
Таким образом, для устойчивости замкнутой системы при устойчивой разомкнутой должно выполняться соотношение (4.31). Это свойство имеет простую геометрическую интерпретацию: вспомогательная частотная характеристика не должна охватывать начало координат
комплексной плоскости. Так как W ( j ) отличается от W0 ( j ) на еди-
ницу, можно строить амплитудно-фазовую характеристику разомкнутой системы, что значительно проще.
Формулировка критерия Найквиста: для устойчивости замкну-
той системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика устойчивой разомкнутой системы при изменении от 0
до не охватывала точку с координатами 1; j0 .
Примеры расположения частотных характеристик, соответствующих устойчивой и неустойчивой замкнутым системам, приведены на рис. 4.16.
|
|
|
Im |
|
|
Im |
|
|
|
|
|
|
|
Im |
|
Im |
|
|
|
|
|||
|
|
|
|
|
|
|
Re |
|
Re |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
– |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
|
|
|
|
|
|
|
|
Re |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W ( j |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
W0 ( j ) |
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
W2 ( j ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.16. Иллюстрация критерия Найквиста:
1 – устойчивые, 2 – неустойчивая замкнутые системы
Разомкнутая система может быть неустойчива, однако это не означает, что неустойчивой будет и замкнутая система. В этой ситуации следует использовать видоизмененную формулировку критерия Найк-
виста: замкнутая система будет устойчива тогда и только тогда, когда амплитудно-фазовая характеристика неустойчивой разомкнутой системы при изменении от 0 до охватывает точку с координатами
1; j0 в положительном направлении r 2 раз, где r – число корней
2 раз, где r – число корней
характеристического уравнения разомкнутой системы с положительной вещественной частью [6].
