6.3. Обработка результатов совместных и совокупных измерений.

При совместных измерениях одновременно измеряют несколько разноименных величин, например: сопротивление терморезистора и его температуру, напряжение и ток исследуемого устройства и т.д. при совокупных измерениях одновременно измеряют несколько одноименных величин, например, различные комбинации измеряемых резисторов , конденсаторов и т.д.

Совместные и совокупные измерения в общем случае описываются уравнением вида:

,

где – известные коэффициенты и непосредственно измеряемые величины;

- искомые неизвестные (например, искомые параметры функциональной зависимости);

m – количество неизвестных.

Обработка совокупных и совместных измерений включает следующие операции:

1. Для эмпирической зависимости строится график расположения эмпирических точек 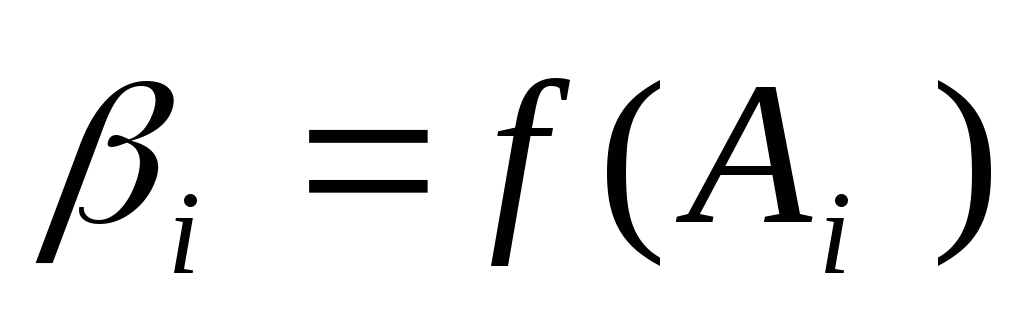. Чтобы уменьшить дополнительную погрешность масштаб графика брать таким, чтобы предельная абсолютная погрешность измерения 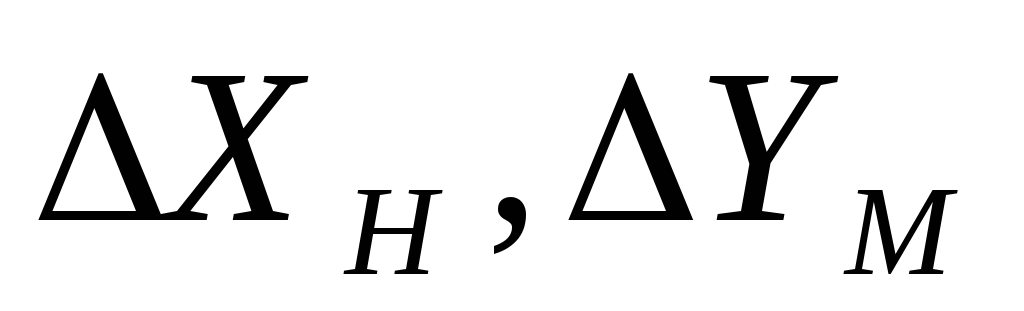изображалась на графике отрезком не меньше 1 мм. и наиболее важная часть графика имела наклон к горизонтальной оси близкий к 45º или 135º.

2. С учетом характера расположения эмпирических точек выбирается вид функциональной зависимости, не менее трех вариантов.

При выборе вида зависимости сравнивают расположения эмпирических точек на графике с графиками простейших функций. Желательно, чтобы аппроксимирующая функция имела вид линейной зависимости или степенного полинома малой степени (не выше трех, четырех).

3. После выбора вида функциональной зависимости определяют оценки искомых параметров, подставив в уравнение результаты i-го измерения и получают систему уравнений вида:

,

которые содержат только неизвестные искомые величины и числовые коэффициенты.

4. Определяются оценки искомых параметров функциональной зависимости с помощью метода наименьших квадратов.

В созданной системе из-за погрешности измерений даже при точно известной зависимости ~ искомыми величинами нельзя найти такие значения неизвестных, при которых одновременно удовлетворяли бы все уравнения, Знак равенства в этих уравнениях носит условный характер, поэтому такие уравнения называются условными.

Поэтому в каждое уравнение введем слагаемое , называемое невязкой и найдем такие оценки искомых величин , при котором сумма квадратов невязок будет минимальна, т.е. в уравнениях:

функция должен иметь минимум.

Этот принцип положен в основу метода наименьших квадратов.

Функция нескольких переменных достигает минимума в точке, где все ее частные производные равны нулю. Поэтому

,

j = 1,2,…,m; n- количество измерений.

Если представляет собой линейную функцию неизвестных величин

получают линейную сумму m нормированных уравнений, составленных по МНК:

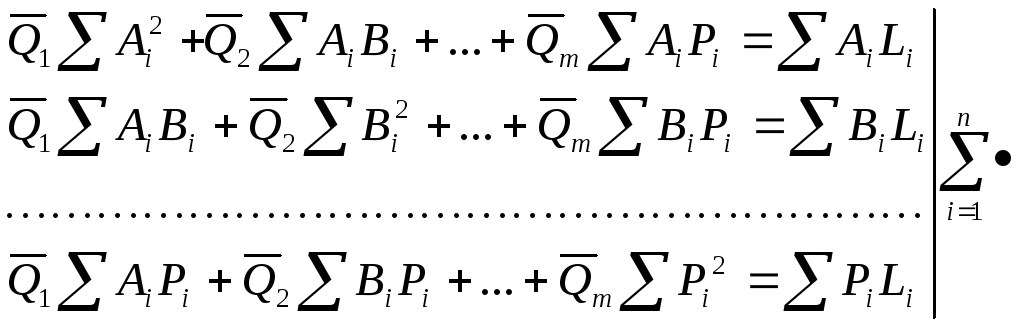
и находятся оценки искомых величин:

или можно решить эту систему с помощью определителей:

- определитель суммы;

- определитель, полученный из определителя путем замены столбца с коэффициентами при неизвестном на столбец с известными членами.

5. Определяются оценки дисперсии искомых параметров и доверительные интервалы их погрешностей.

Для этого из полученных результатов выбирают погрешность того измерения, погрешность которого превышает остальные. Эту измеренную величину выделяют в свободный член , а результаты считаются точными. В этом случае дисперсии:

где - алгебраические дополнении элементов.

- дисперсии условных уравнений.

- невязка условного уравнения, полученные при подстановке в него оценок .

Доверительные интервалы определяют на основе распределения Стьюдента.