
- •1. Предмет и задачи метрологии
- •1.1.Основные определения
- •1.2.Классификация измерений
- •1.3.Основные положения метрологического обеспечения измерений
- •1.4.Эталоны единиц электрических величин
- •1.5. Методики выполнения измерений
- •2.Методы и средства измерений
- •2.1 Методы измерений
- •2.2. Средства измерений
- •2.3. Обозначение средств измерений
- •2.4. Метрологические характеристики средств измерений
- •2.5. Нормирование погрешностей средств измерений
- •2.6 Обобщенные структурные схемы измерительных приборов
- •2.7 Факторы, ограничивающие точность измерения
- •2.8 Методы повышения точности приборов
- •Вопросы для самоконтроля
- •3. Погрешности измерений и их математическое описание
- •3.1. Классификация погрешностей
- •4.Математическое описание случайных погрешностей.
- •4.1. Общие сведения
- •4.2. Определение грубых погрешностей.
- •4.3. Идентификация формы закона распределения погрешностей.
- •4.4. Основные законы распределения случайной погрешности.
- •5.Учет систематической погрешности и способы ее уменьшения.
- •5.1.Неисключенная систематическая погрешность
- •Обеспечиваются нормированием условий работы средств измерений;
- •6. Обработка результатов наблюдений.
- •6.1. Обработка результатов прямых, многократных, неравноточных, наблюдений.
- •6.2. Обработка результатов косвенных измерений.
- •6.3. Обработка результатов совместных и совокупных измерений.
- •7. План измерений и методы его измерения.
-
Обеспечиваются нормированием условий работы средств измерений;
-
Измеряемая величина одновременно подается на оба средства измерения (рабочее, образцовое), причем случайная погрешность образцового в 3 – 5 раз меньше случайной погрешности рабочего средства измерения. Т.к.
![]()
и заверяются
показания образцового
![]() и рабочего средства измерения
и рабочего средства измерения
![]() .
.
-
Измерение повторяется N раз.
Определяется погрешность каждого наблюдения:
![]() ,
,
которая содержит в общем случае систематическую и случайную составляющие:
![]()
-
Вычисляется систематическая погрешность средств измерения:
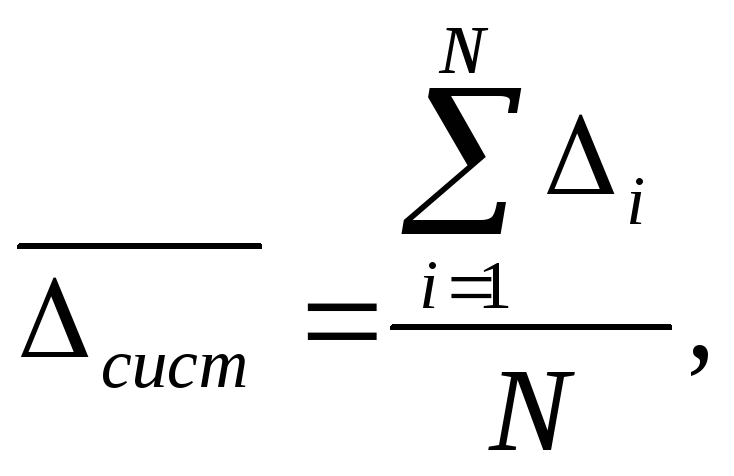
т.к. случайные
погрешности
![]() имеют
разные знаки, поэтому компенсируются:
имеют
разные знаки, поэтому компенсируются:
![]() .
.
-
Вычисляют случайные погрешности каждого измерения:
![]()
и оценивают среднее квадратичное значение случайной погрешности:
![]() .
.
-
Определяется доверительный интервал случайной погрешности:
![]() ,
,
где
![]() -
коэффициент зависящий от функции
распределения и доверительной вероятности.
-
коэффициент зависящий от функции
распределения и доверительной вероятности.
-
Т.о. погрешность средств измерений находится в интервале:
![]()
6. Обработка результатов наблюдений.
6.1. Обработка результатов прямых, многократных, неравноточных, наблюдений.
Пусть имеется m групп независимых и разных по точности наблюдений одной и той же величины.
И в каждой j-ой группе
точности вычислены результаты измерений
![]() и СКО –
и СКО –
![]() .
.
Тогда:
-
Вычисляются весовые коэффициенты (степень доверия к оценкам
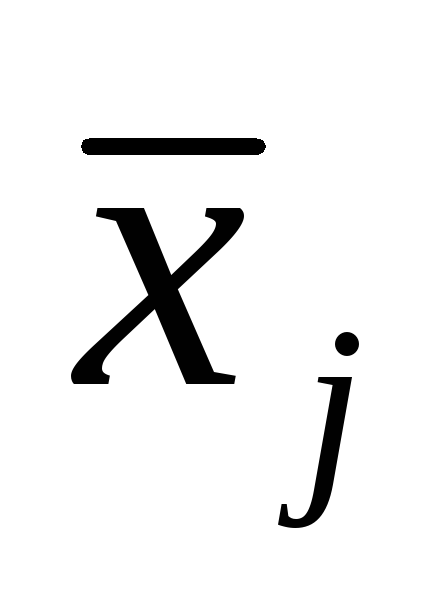 ).
).
![]()
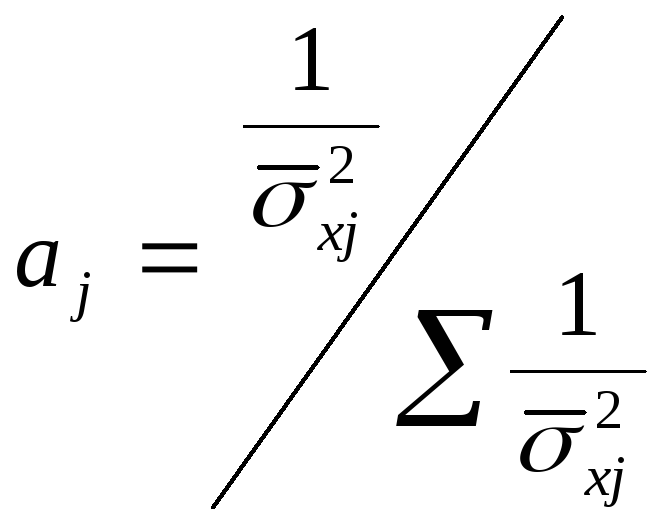 .
.
Причем,
![]() .
.
-
Вычисляются средне взвешенное значение наблюдений:
![]() ,
,
где
![]() -
математическое ожидание независимых
наблюдений.
-
математическое ожидание независимых
наблюдений.
-
Среднеквадратичное отклонение результата неравноточных наблюдений:
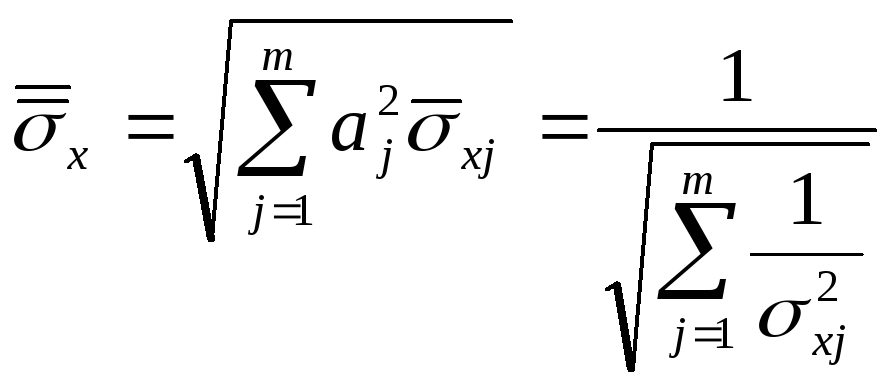 .
.
-
Находят границы доверительного интервала для случайной погрешности средневзвешенного значения при заданной доверительной вероятности и общем числе наблюдений:
![]() ,
,
где
![]() - число наблюдений в j-ой
группе.
- число наблюдений в j-ой
группе.
-
Полученный результат дописывается в виде:
![]() .
.
6.2. Обработка результатов косвенных измерений.
При косвенных измерениях искомое
значение измеряемой величины у
(функции) находят по результатам
прямых измерений ряда других величин
![]() ,
называемых аргументами и связанных с
измеряемой величиной известной
зависимостью:
,
называемых аргументами и связанных с
измеряемой величиной известной
зависимостью:
![]() ,
(1)
,
(1)
где m – число аргументов.
Обработка результатов косвенных измерений сводится к следующему:
-
Используя статическую обработку прямых многократных наблюдений для каждого аргумента определяют математическое ожидание
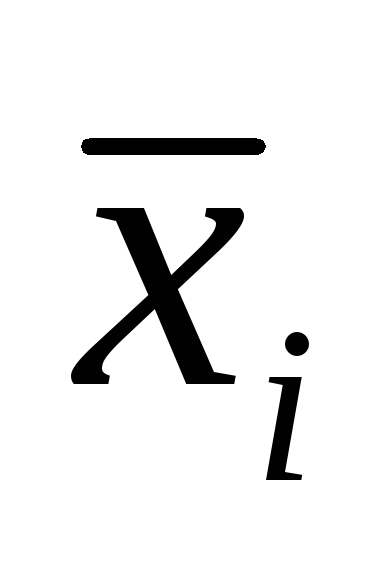 ,
,
 и
после внесения поправок в известные
математические погрешности – остатки
НСП -
и
после внесения поправок в известные
математические погрешности – остатки
НСП -
 .
. -
Находят оценку искомой величины:
![]() .
.
-
Вычисляют коэффициенты влияния (веса).
Т.к. каждое измерение
![]() ,
,
Разложив (1) в ряд Тейлора и учитывая только члены первой степени, получим:
![]()
Получим коэффициенты влияния:
![]() ,
,
а погрешность косвенного измерения:
![]() .
.
-
Определяется ско случайной погрешности. При условии, что все
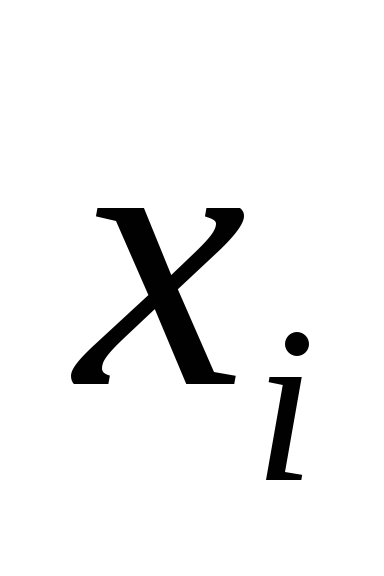 измерения независимые (существуют
разные средства измерения).
измерения независимые (существуют
разные средства измерения).
![]() .
.
Если
![]() - зависимые, то:
- зависимые, то:
![]() ,
,
где
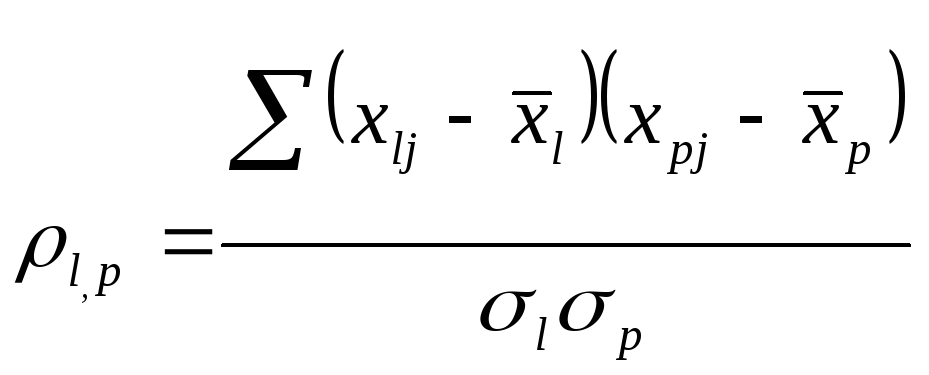 - коэффициент корреляции между случайными
погрешностями l и p.
- коэффициент корреляции между случайными
погрешностями l и p.
![]() .
.
-
Определяется систематическая погрешность результата измерения, вызванная наличием НСП прямых измерений:
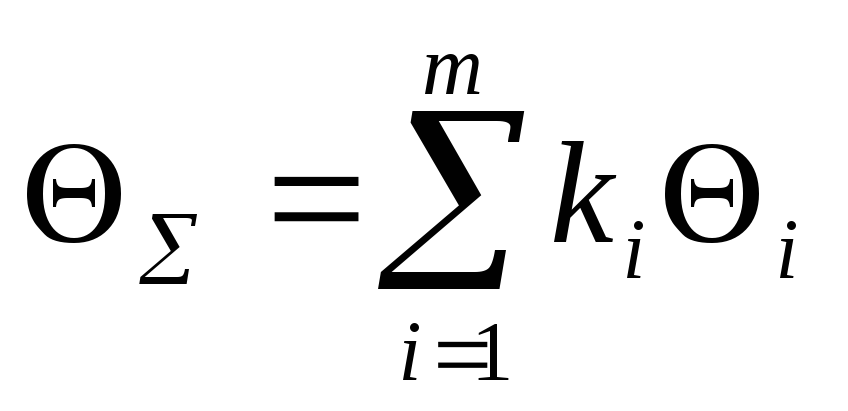 ,
,
если границы
![]() известны, то распределение считается
равномерным.
известны, то распределение считается
равномерным.
-
Находится доверительный интервал случайной погрешности результата измерения при заданной доверительной вероятности:
![]() .
.
-
Проверяют соотношение величин
 и
и
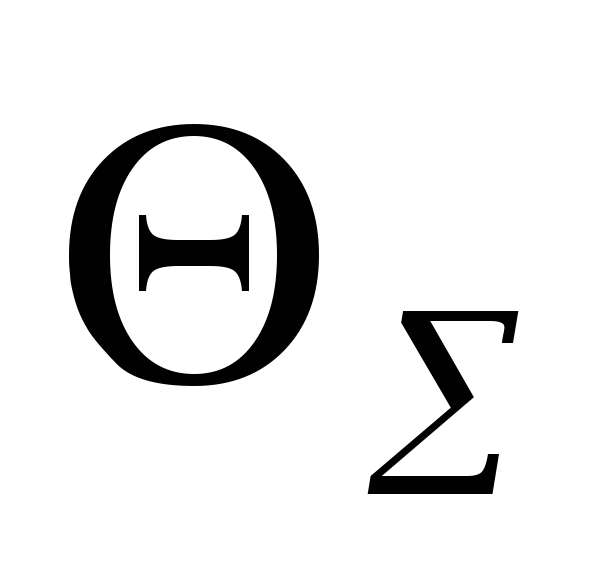 как
для прямых многократных наблюдений.
как
для прямых многократных наблюдений. -
Результат косвенного измерения (при n>25-30) записывают в виде:
![]() .
.
