Анализ устойчивости сау с учетом запаздывания

Звено запаздывания

Хвх ? Хвых

Запаздывание –явление, когда звено реагирует только через время t после подачи команды

ПФРСАУ

t

Аппериодическое звено:

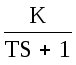
Хвх 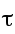Хвых

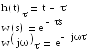
Хвых(s)=W(s) Хвх(s)

Если брать по времени, подав на вход ступенчатое воздействие, то на выходе будет экспонента, сдвинутая на τ относительно нуля.

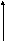
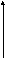
Соберем все в одну систему с учетом запаздывания

g(t) W1 W2 W3 W4 Xвых

Если бы не было запаздывания

Сиситема без запаздывания называется предельной

С учетом запаздывания

ПФРСАУ – передаточная функция разомкнутой САУ с учетом запаздывания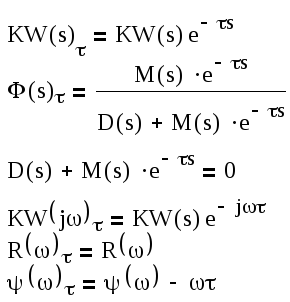

ПФЗСАУ – передаточная функция замкнутой САУ с учетом запаздывания

ХУЗСАУ – характеристическое уравнение замкнутой САУ с учетом запаздывания

ЧХРСАУ – частотная характеристика разомкнутой САУ с учетом запаздывания

АХРСАУ – амплитудная характеристика разомкнутой САУ с учетом запаздыания

ФХРСАУ – фазовая характеристика разомкнутой САУ с учетом запаздыания

При каждом значении ω появляется дополнительный сдвиг по фазе, равный ωt.

Системы с запаздыванием не являются минимально фазовыми

Запаздывание вызывает уменьшение устойчивости системы.

Проверим это с помощью критерия устойчивости:

“левые”

Трансцендентное уравнение

Какой же критерий Найквиста отражен здесь?

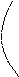
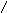
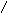
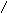
Каждый вектор ЧХ с учетом запаздывания, оставаясь по модулю тем же, будет поворачиваться на угол ωτ

Запаздывание может «съесть» запасы устойчивости

Поэтому нужно найти допустимое значение запаздывания – критическое запаздывание – такое запаздывание, при котором система выходит за границу устойчивости.

Имелся запас по фазе γ

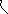
Если γ = 0, то система находится на границе устойчивости

Если:

1. _кр - система остается устойчивой при наличии запаздывания

2. _кр - система на границе устойчивости

3. _кр – система неустойчива

Метод “D-разбиения”

(Метод Нейморка)

Область

D(n)

о

Все корни

’’левые’’

о

о

о

М_i

0

Имеется n-мерное пространство.

По каждому измерению этого пространства будем откладывать коэффициент характеристического уравнения и образуем «пространство коэффициентов характеристического уравнения».

Каждая точка в этом n-мерном пространстве будет соответствовать своему характеристическому уравнению.

Предположим, что во всех точках в этой области, все корни х и у будут левыми. Эта область – область устойчивости в пространстве коэффициентов уравнения.

Этих областей может быть несколько.

Определим границы областей устойчивости:

Все пространство разбиваем на отдельные области и из этих областей какие-то являются устойчивыми

Условие границы S = jω

Дано:

- уравнение границы “D”

D(n) – область устойчивости (все корни «левые»)

Построение области устойчивости по параметрам САУ

Плоскость первого параметра

1.

Необходимо найти границы изменения q, которые находятся на границе устойчивости.

Разрешаем уравнение относительно q.

2.

- условие границы для разбиения.

3. Задаемся значением ω = 0 ÷ ∞ и строим U(ω) и V(ω)

4. Задаемся ω = 0 ÷ - ∞. Эта зависимость будет зеркальным отображением для ω = 0 ÷ + ∞

Определяем область D

2

q_крmin

1

4

3

D(n)?

q_крmax

5. Нанесем штриховку по определенному правилу:

Двигаясь вдоль мнимой оси от - ∞ до + ∞ наносим штриховку слева.

Никакие точки пересечения не должны смущать.

6. Выделяем «претендентов» - все области, имеющие максимальную внутреннюю штриховку.

7. Проверяем на устойчивость любую точку «претендента» по любому критерию.

8. Находим D(n)

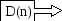
Е

нет

сли , то САУ «структурно не устойчива» - система вообще не может быть устойчива

Плоскость 2-х параметров

1.

2.

3. Метод Крамера

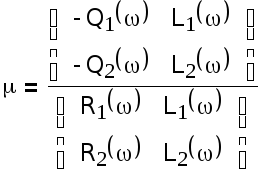
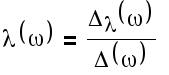
4. Правая система координат

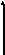
0

5. ω = 0 ÷ + ∞ строим

Т.к. λ и μ – четные, то граница получается как бы двойная, т.е. каждая точка ±

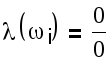
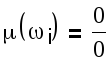
6. Если или , то ω_i – «особая точка». Решением в этом

случае будет прямая, проходящая через «особую точку», которая называется «особая прямая».

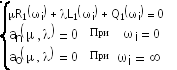
7. Штрихуем границу D-разбиения:

а) штриховка находится слева, если гавный определитель системы Δ при -∞ будет больше нуля, а если меньше нуля – справа.

б) При прохождении особой точки, штриховка меняется на обратную

в) Особые прямые штрихуются.

Штриховка особой прямой зависит от направления штриховки основной границы. В окрестностях особой точки она направлена в ту же сторону, что и штриховка основной границы.

г) Штриховка наносится сразу двойной

д) Особая прямая, соответствующая ω = 0 штрихуется одинарной штриховкой

!

Никакие точки пересечения не меняют направления штриховки. Его могут изменить только особые точки.

8. Выделение «претендентов»

9. Проверка на устойчивость по критериям Гурвица.

10. Окончательно выделяем D(n)

Окончательно надо остановиться на той области устойчивости, которая соответствует вопросу реализации.

Особая прямая

Пример

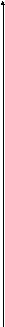
m=2

9

.

7

6

4

2

3

5

0

m=4

m=2

m=4

m=0

m=3

m=2

m=0

1

8

ОП

Особая прямая