Устойчивость сау

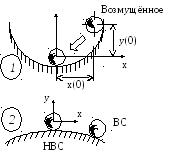
Невозмущённое состояние (равновесия)

ДВИЖЕНИЕ:

невозмущённое,

(заданное)

возмущённое

… Никогда не надо

умирать раньше

смерти…

А. М. Ляпунов

НДВ устойчиво

НВД

НВД устойчиво по отношению к переменной x_i, если при всяком , как бы мало оно ни было, можно найти другое такое, что для всех удовлетворяющих при условию *, возмущенное движение при t>0 будет удовлетворять неравенству

- область

- область допустимых отклонений.

Выводы:

1. Об устойчивости НВД судят по характеру .

2. .

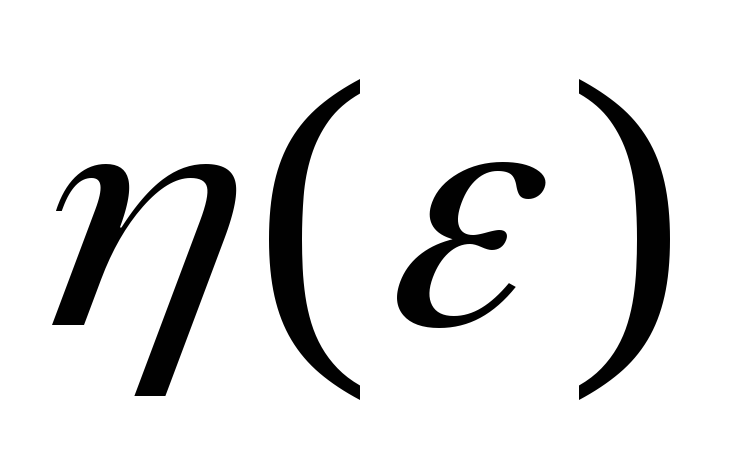3. Условия ** накладываются при .

4. В общем случае не требуется ***, достаточно **.

5. Устойчивость по Ляпунову, это устойчивость в “малом”.

6. Определение носит качественный характер.

7. Механический смысл определе-ния устойчивости в характерис-тике прочности и сопротивляемости действующим возмущениям.

А.М. Ляпунов

1892 – докторская диссертация “Общая задача об устойчивости движения” .

I. Метод исследования Ляпунова:

Отыскание общего или частного решений уравнений ВД - исследование

ние линеа-ризованных уравнений (уравнений первого приближения)

I I. Прямой метод исследования Ляпунова:

Основан на поиске и свойствах специальных функций Ляпунова.

где

Исследование устойчивости НВД по уравнениям первого приближения.

(Первая метода А.М. Ляпунова)

Дано: диф. уравнение линеариз. САУ

корни XY

Уравнение ВД:

где - корни

Если - “левые”, т.е. ,

т

Условие АСУ условию

о

Вывод:

АСУ – асимптотическая устойчивость

Выводы:

совокупность

условий

Теоремы А.М. Ляпунова

Теорема 1. Если все ХУПП (характеристическое уравнение первого приближения) имеют , то НВДАСУ независимо от вида отброшенных при линеаризации нелинейных членов (высших членов ряда Тейлора) разложения.

Теорема 2. Если среди ХУПП есть хотя бы один с, то НВДНУ…

Теорема 3. Критический случай.

Если среди ХУПП есть хотя бы один с , то для исследования ус-сти

НВД следует использовать исходные нелинейные уравнения, т.е. устойчивость зависит и от вида отброшенных при линеаризации членов разложения порядка выше первого.

Прямая метода А.М. Ляпунова.

[1] стр. 65-73

Теоремы А.М. Ляпунова позволяют сделать вывод, при каких условиях заключения об устойчивости, полученные для линеаризованной системы, сохраняют силу и для исходной нелинейной САУ.