Математическая модель сау

ММ САУ «В-В»

 = Х_вых

f(t) = Х_вх

_зад = 0

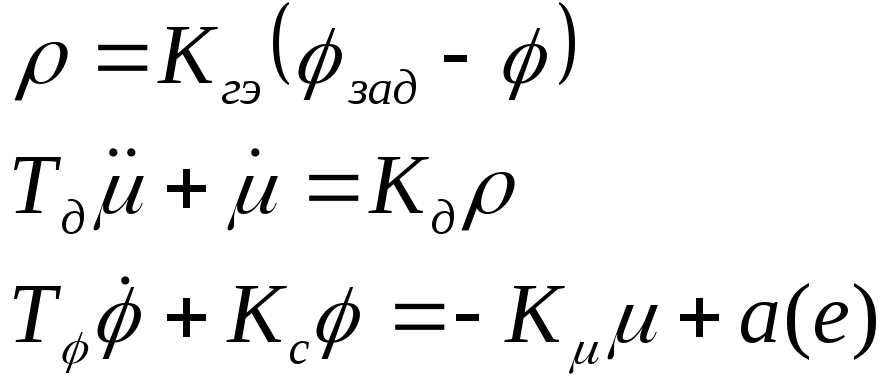
Приведем «в порядок» и запишем в операторной форме:

Как изменятся выходные координаты при воздействии?

Хвх

Хвых

Решаем систему уравнений относительно исходных координат.

Результат должен быть вида:

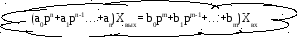
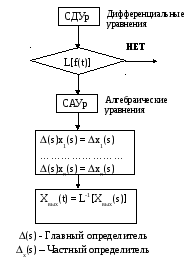
Решение уравнений динамического состояния сау

Методы Решешения:

1. Операторный (не будем использовать)

2. Преобразование Фурье

- оригинал

- изображение функции по Фурье

Ограничения (чтобы функцию разложить по Фурье должны быть:

а. Нулевые граничные условия

б. Условия Дирихле

(когда известно, что функции близки к гармоническим)

3. Преобразования Лапласа

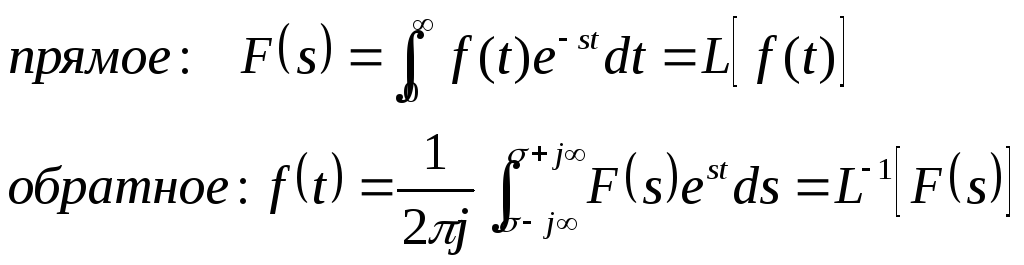
F(s) – изображение

f(t) – оригинал

F(s)  f(t)

Особенности:

1. Начальные условия любые.

2. Сложные правые части.

3. Не выполнение условий Дирихле. Например: 1[t], sin(wt)…

Преобразования Лапласа позволяют:

1. Получать аналитические решения.

2. Широко использовать опыт (справочники, таблицы, …)

3. Решать конечные задачи (когда не интересует промежуточные решения)

4. Решать задачи анализа и синтеза и т.д. и т.п.

Основные свойства:

… Отвлеченные истины следует излагать чистым языком, просто и благородно… Фурье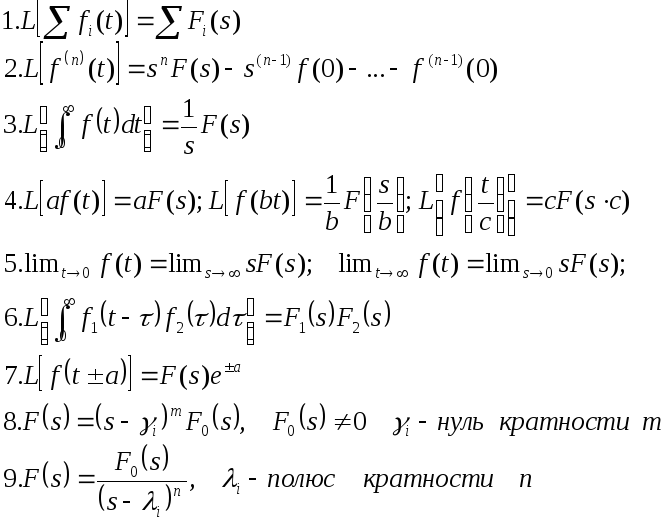

Оператор

Комплексная переменная

Имеем ММ в виде системы линейных уравнений. Преобразуем все функции по Лапласу в этом сценарии:

А

Жан Батист Жозеф Фурье 1768-1830 – математик, физик, Почетный член Петербург. АН (1829): деф. Ур.; тригонометрические ряды и преобразования.

лгоритм решения:

Т.е. система диф. Уравнений преобразуется в систему алгебраических уравнений.

… Ну и что ? А то …

Формулы разложения (Хависайда)

Дано:

Требуется:

1.

S_к – простые действительные корни полинома В(S) = В₁(S) = 0

2.

3.

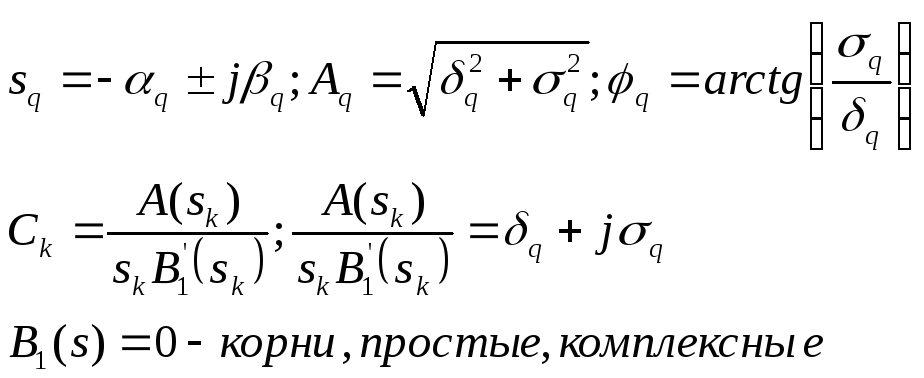
Примеры:

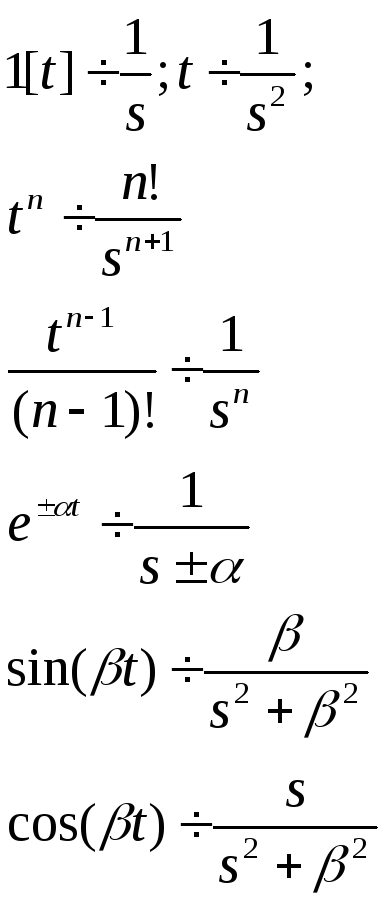
и т.д.

(s) = D(s) – полином (левая часть)

_x(s)=M(s)Xвх(s)+R(0)

M(s) – полином (правая часть)

Xвх(s) – изображение входного воздействия

R(0) – ненулевые начальные условия

Характеристическое уравнение системы

М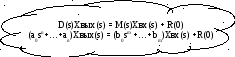атематическая модель системы управления

Уравнение переходного процесса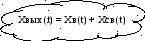

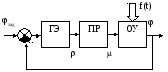
Преобразуем по Лапласу систему (как пример можно взять вращение вала двигателя)

(T_s+Kc) (s)+K_(s)=T_(0)+F(s)

– K_2Э(s) + (s) = 0

-K_g(s) + (T_gs²+s)(s) = T_gs(0) + T_g(0) + (0)

Запишем главный определитель:

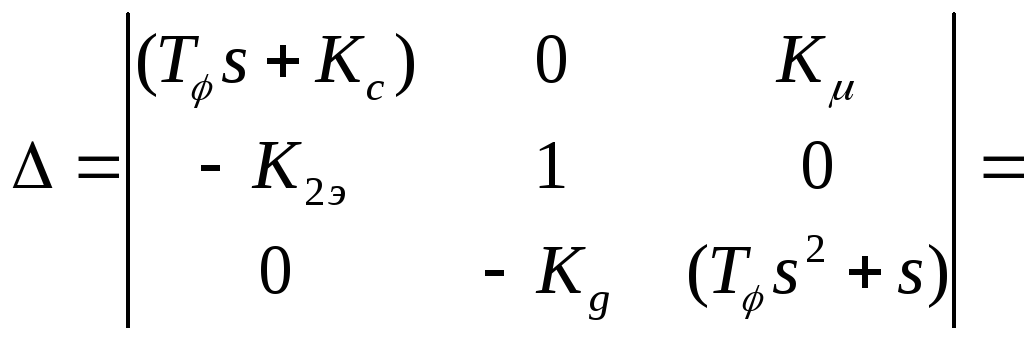решаем каким-либо методом = a₀s³ + a₁s² +a₂s +a₃

() () ()

а₀ = T_T_g

a₁ = T_ +K_C Tg

a₂ = _KC

a₃ = K_K_2ЭK_g

Частные определители:

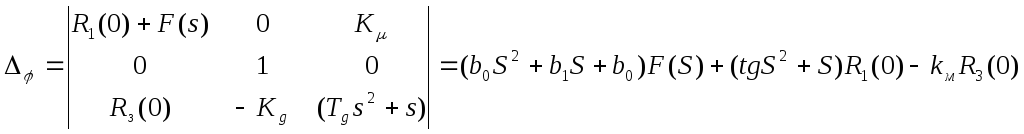
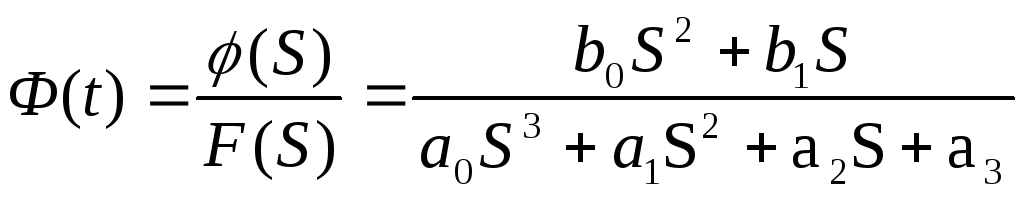
Передаточные функции

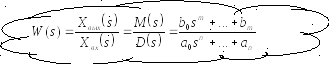
Передаточная функция – отношение выходной координаты к изображению входной при нулевых начальных условиях

Основные свойства

1. n > m  УФР (для физически реализуемых систем) – условие физической реализуемости.

2. Х_вых(s) = W(s)Х_вх(S)

Передаточная функция не зависит от входного воздействия Х_вх(S) и нулевых начальных условий R(0)

Определяет свойства а не состояние!

3. M(s) = 0  _i  нули передаточной функции

D(s) = 0  _i  полюса

4. _i

«левые»  САУ МФ

_i

Комплексные величины.

5. a_i Re

и  САУ стационарная

b_i Const

Если известна W(s) каждого элемента, то как найти ПФ соединения элементов?