Определение передаточных звеньев группы звеньев

Если известна W(s) каждого элемента, то как найти ПФ соединения элементов?

ПФ 1 группы:

2 группы

3 группы “+” для отрицательной обратной связи

“-“ для положительной обратной связи

Передаточные функции сау

Предположим, что мы имеем структурную схему

W₀ – ПФ объекта управления

Передаточная функция САУ в разомкнутом состоянии

Передаточная функция САУ в режиме управления

Передаточная функция САУ в режиме стабилизации

Передаточная функция САУ по ошибке

Математическа модель через ПФ

- учет ненулевых условий

[1+KW(s)]Xвых(s) = W_регW₀G(s)+W_f(s)+R(0)

(S) _х(s)

1+KW(s) = (S) - главный определитель системы

x(s) - частный определитель системы

Характеристическое уравнение САУ в замкнутом состоянии

Полюса – такие значения ???, где функция обращается в 0 или ∞

Примечание:

ХУ САУ в разомкнутом состоянии

_i

Число корней в замкнутом и разомкнутом состоянии одно и то же.

Переходная функция системы

h(t) – переходная функция – реакция системы на единичное ступенчатое воздействие

t_пп – время переходного процесса – то время, после которого, гафик, попав в трубку точности, больше из нее не выходит.

Х_вых(s) = W(s)s^-1 = H(s)

H(s) – изображение переходной функции

Вид переходной функции определяет характер и вид переходного процесса

Форма и характер переходного процесса:

1. Монотонный

2. Колебательный периодический.

3. Колебательный апериодический.

Степень колебательности

Перерегулирование

Режим стабилизации

Импульсная переходная функция

Х_вх = 1’[t] – единичный импульс

K_и(t) – реакция системы на единичный ступенчатый импульс

Импульсная функция – оригинал от передаточной функции

Импульсная переходная функция – дифференциал от переходной функции.

Определение реакции на воздействие произвольного типа

Интеграл Дюамеля !!!

ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ

САУ

X_вх = Х_вых=

= Аsint = B()sin[t+φ(ω)]

А =const

АЧХ ω = var

φ(ω)

ФЧХ

Чем шире полоса пропускания, тем t_пп меньше

_пп – полоса пропускания

_рез – резонансная частота

Объединение характеристик на комплексной плоскости

Предположим, дано уравнение в операторной форме

D(p) X_вых = M(p) Х_вх

Пусть: Х_вх = Аsint = J _m Ae^jωt

Тогда: Хвых = B()sint[t+φ(ω)] = J _m B()e^{j[t+φ(ω)]}

Преобразования Фурье

p = j

т.е. D(j)B()e^jωt e^{j φ(ω)} = M(j)Ae^jωt

Основные свойства АФЧХ

1.

2. Частотная характеристика есть функция комплексного переменного

Номограммы замыкания

3. Обратная ЧХ (иногда удобна)

4. Интеграл Фурье

5. Пусть есть передаточная функция

Все _i и_i

“левые”

а

Один _к “правый”

)

б)

Фазовые сдвиги всегда меньше, если все нули левые => минимально фазовая система (МФС)

Все ЧХ находятся в однозначной зависимости в МФС

МФ САУ R(ω)  φ (ω)

P(ω)  Q(ω)

6. ЧХ для отрицательного диапазона частот – зеркальное отображение для положительного диапазона частот

7. Условие физической реализуемости

_{Если система статичная, то ЧХ должна начинаться из нуля}

Если система астатичная, то ЧХ начинается из бесконечности

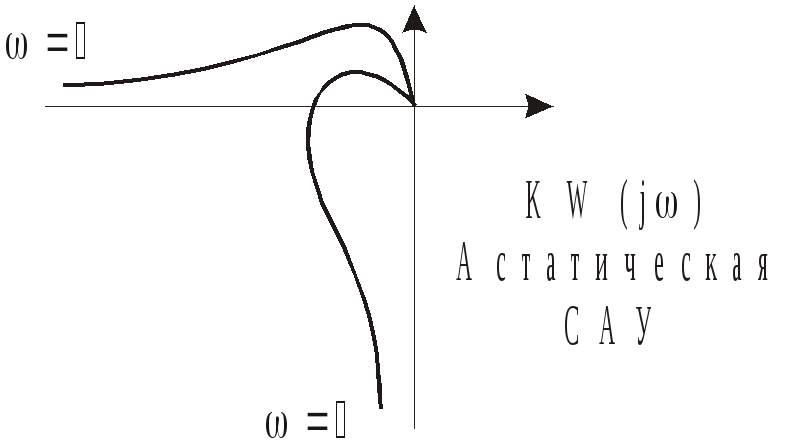
8. ЧХ группы соединенных элементов

ВЕКТОР !!! Речь идет именно о векторах.

U() – действительная частотная характеристика САУ в разомкнутом состоянии

P() – действительная частотная характеристика САУ в замкнутом состоянии

V() – мнимая частотная характеристика САУ в разомкнутом состоянии

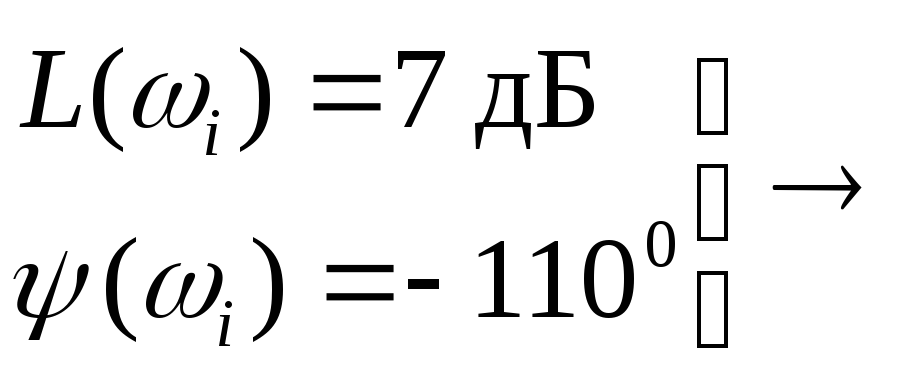
3

ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ

ЛАЧХ

ЛФЧХ

0

1 2 3 4 5 6 7 8 9 10 20 30

декада

октава

октава

декада

октава

5

-5

дБ L()

lg(ω)

ω

Изменение частоты в 2 раза - октава

_сопр – частота сопряжения

_ср – частота среза

При последовательном соединении:

Динамические характеристики САУ

[1] Ст. 42-54