
- •Властивості
- •Властивості
- •16. Зростаючі й спадні функції
- •Екстремуми функції
- •19. Скалярний добуток векторів
- •21. Перпендикуляр і похила
- •Властивості похилих
- •Перпендикуляр і похила
- •Теорема про триперпендикуляри
- •23. Паралелепіпед
- •26. Конус
- •27. Зрізаний конус
- •28. Куля
- •Площа круга
- •29. Основні поняття теорії імовірностей
- •Формула Бернуллі
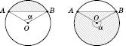
Площа круга
 S =pR2
Круговим
сектором називається
частина круга, яка лежить усередині
відповідного центрального кута (див.
рисунок).
Sсект
S =pR2
Круговим
сектором називається
частина круга, яка лежить усередині
відповідного центрального кута (див.
рисунок).
Sсект ,
де
,
де  —
градусна міра відповідного центрального
кута.
Круговим
сегментом називається
спільна частина круга й півплощини.
На
рисунку нижче зліва зображений круговий
сегмент, якщо
—
градусна міра відповідного центрального
кута.
Круговим
сегментом називається
спільна частина круга й півплощини.
На
рисунку нижче зліва зображений круговий
сегмент, якщо  ;
на рисунку справа — круговий сегмент,
якщо
;
на рисунку справа — круговий сегмент,
якщо  .
.

29. Основні поняття теорії імовірностей
Подія —
це будь-яке явище, про яке можна сказати,
що воно відбувається чи не відбувається.
Подія
відбувається внаслідок випробування.
Події позначають великими буквами
латинського алфавіту  .
Випадковою
подією називається
подія, яка може відбутися чи не відбутися
під час здійснення певного
випробування. Масовими називають
однорідні події, що спостерігаються
за певних умов і які можуть бути
відтворені необмежену кількість
разів.
Масовими
вважають і ті події, для яких відповідні
випробування не можна відтворити, але
є можливість спостерігати аналогічні
випробування у великій кількості.
Множина подій утворюєповну
групу подій,
якщо внаслідок кожного випробування
хоч одна із цих подій напевно
відбудеться.
Події
називаються попарно
несумісними в
даному випробуванні, якщо ніякі дві з
них не можуть відбутися
разом.
Вірогідною називається
подія, яка внаслідок випробування
обов’язково має відбутися, а неможливою —
подія, яка внаслідок даного випробування
не може відбутися.
Імовірність —
числова характеристика можливості
появи випадкової події за певної умови,
яка може бути відтворена необмежену
кількість разів.
Імовірністю
випадкової події називається
відношення кількості подій, які сприяють
цій події, і кількості всіх рівноможливих
несумісних подій, які утворюють повну
групу подій під час певного
випробування.
Позначення:
.
Випадковою
подією називається
подія, яка може відбутися чи не відбутися
під час здійснення певного
випробування. Масовими називають
однорідні події, що спостерігаються
за певних умов і які можуть бути
відтворені необмежену кількість
разів.
Масовими
вважають і ті події, для яких відповідні
випробування не можна відтворити, але
є можливість спостерігати аналогічні
випробування у великій кількості.
Множина подій утворюєповну
групу подій,
якщо внаслідок кожного випробування
хоч одна із цих подій напевно
відбудеться.
Події
називаються попарно
несумісними в
даному випробуванні, якщо ніякі дві з
них не можуть відбутися
разом.
Вірогідною називається
подія, яка внаслідок випробування
обов’язково має відбутися, а неможливою —
подія, яка внаслідок даного випробування
не може відбутися.
Імовірність —
числова характеристика можливості
появи випадкової події за певної умови,
яка може бути відтворена необмежену
кількість разів.
Імовірністю
випадкової події називається
відношення кількості подій, які сприяють
цій події, і кількості всіх рівноможливих
несумісних подій, які утворюють повну
групу подій під час певного
випробування.
Позначення: 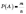 ,
де n —
загальна кількість рівноможливих і
несумісних подій, які утворюють повну
групу, m —
число елементарних подій, які сприяють
події A.
Сумою
подійA і B називається
подія C,
яка полягає у здійсненні під час
одиночного випробування або події A,
або події B,
або обох разом.
Позначення:
,
де n —
загальна кількість рівноможливих і
несумісних подій, які утворюють повну
групу, m —
число елементарних подій, які сприяють
події A.
Сумою
подійA і B називається
подія C,
яка полягає у здійсненні під час
одиночного випробування або події A,
або події B,
або обох разом.
Позначення:  ,
або
,
або  .
Теорема
1. Імовірність суми двох несумісних
подій дорівнює сумі ймовірностей цих
подій, тобто
.
Теорема
1. Імовірність суми двох несумісних
подій дорівнює сумі ймовірностей цих
подій, тобто 
 .
Наслідки
1.
Сума ймовірностей несумісних подій,
що утворюють повну групу, дорівнює
1.
2.
Сума ймовірностей протилежних подій
дорівнює 1, тобто
.
Наслідки
1.
Сума ймовірностей несумісних подій,
що утворюють повну групу, дорівнює
1.
2.
Сума ймовірностей протилежних подій
дорівнює 1, тобто  .
Дві
події називаються протилежними,
якщо одна, і тільки одна, з них обов’язково
здійсниться в даному випробуванні.
Добутком
двох подійA і B називається
подія С,
що полягає у здійсненні під час одиничного
випробування і події A,
і події B.
Позначення:
.
Дві
події називаються протилежними,
якщо одна, і тільки одна, з них обов’язково
здійсниться в даному випробуванні.
Добутком
двох подійA і B називається
подія С,
що полягає у здійсненні під час одиничного
випробування і події A,
і події B.
Позначення:  ,
або
,
або  .
Подія А називається незалежною відподії B,
якщо ймовірність події А не
залежить від того, відбулась чи ні
подія B.
Теорема
2. Імовірність добутку двох незалежних
подій A і B дорівнює
добутку ймовірностей цих подій,
тобто
.
Подія А називається незалежною відподії B,
якщо ймовірність події А не
залежить від того, відбулась чи ні
подія B.
Теорема
2. Імовірність добутку двох незалежних
подій A і B дорівнює
добутку ймовірностей цих подій,
тобто  .
Теорема
3. Якщо події
.
Теорема
3. Якщо події  ,
,  ,
... ,
,
... ,  —
взаємно незалежні, то ймовірність
здійснення принаймні однієї з них може
бути виражена через імовірність цих
подій за формулою
—
взаємно незалежні, то ймовірність
здійснення принаймні однієї з них може
бути виражена через імовірність цих
подій за формулою
 .
Наслідок.
Якщо
.
Наслідок.
Якщо  ,
то
,
то  .
Взаємно
незалежними називаються
такі випробування, у яких імовірність
результату кожного з них не залежить
від того, які результати має чи матиме
решта випробувань.
.
Взаємно
незалежними називаються
такі випробування, у яких імовірність
результату кожного з них не залежить
від того, які результати має чи матиме
решта випробувань.
