
- •Лекция № 21. Фильтрование. Общие сведения.
- •Уравнения фильтрования
- •Лекция № 22. Наибольшая производительность фильтров.
- •Экономически оптимальная продолжительность цикла фильтрования.
- •Расчет фильтров
- •Лекция № 23. Центрифугирование. Основные положения.
- •Центробежная сила и фактор разделения
- •Процессы в отстойных центрифугах
- •Процессы в фильтрующих центрифугах
- •Расчет центрифуг
- •Лекция № 24. Разделение газовых систем (очистка газов). Общие сведения.
- •Гравитационная очистка газов
- •Очистка газов фильтрованием
- •Мокрая очистка газов
- •Электрическая очистка газов
- •Сравнительные характеристики и выбор газоочистительной аппаратуры
- •Лекция № 25. Перемешивание в жидких средах. Общие сведения.
- •Механическое перемешивание
- •Механические перемешивающие устройства
Экономически оптимальная продолжительность цикла фильтрования.
Работа фильтров периодического действия при наибольшей производительности обычно не совпадает с экономически целесообразными условиями фильтрования. Это связано с тем, что для достижения наибольшей производительности фильтра необходимо довольно часто производить вспомогательную операцию разгрузки осадка, которая, как правило, требует определенной затраты труда или энергии.
Рассмотрим
приближенный, но практически применимый
способ нахождения экономически
оптимальной продолжительности цикла
фильтрования при постоянной разности
давлений. Примем, что для некоторых
условий работы фильтра величина А,
вычисленная
по уравнению (2), равна 1,266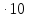 -6
м2/сек,
а
-6
м2/сек,
а
 = 600 сек.
Воспользовавшись
уравнением (3), определим для ряда значений
= 600 сек.
Воспользовавшись
уравнением (3), определим для ряда значений
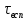 в пределах 0 - 5000 сек
соответствующие
величины
в пределах 0 - 5000 сек
соответствующие
величины
 ,
нанесем найденные таким образом точки
на график в координатах
,
нанесем найденные таким образом точки
на график в координатах
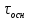 —
—
 (рис. 1) и соединим эти точки плавной
кривой. Как и следовало ожидать, из
указанного графика видно, что максимальное
значение
(рис. 1) и соединим эти точки плавной
кривой. Как и следовало ожидать, из
указанного графика видно, что максимальное
значение
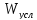 = 2,29
= 2,29
 10-5
м/сек
соответствует
10-5
м/сек
соответствует
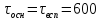 сек.
Кроме
того, из рассматриваемого графика видно,
что кривая
сек.
Кроме
того, из рассматриваемого графика видно,
что кривая
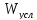 =f(
=f(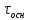 )
имеет сравнительно небольшой наклон
вправо от максимума. Это позволяет,
значительно увеличив продолжительность
основных операций, обеспечить работу
фильтра при достаточно высокой
производительности. Так, при увеличении
)
имеет сравнительно небольшой наклон
вправо от максимума. Это позволяет,
значительно увеличив продолжительность
основных операций, обеспечить работу
фильтра при достаточно высокой
производительности. Так, при увеличении
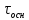 от
600 до 3000 сек,
в
результате чего операции разгрузки
осадка будут производиться в 5 раз реже,
величина
от
600 до 3000 сек,
в
результате чего операции разгрузки
осадка будут производиться в 5 раз реже,
величина
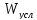 уменьшается от 2,29
уменьшается от 2,29
 10-5
до 1,72
10-5
до 1,72
 10-5
м/сек,
т.
е. только на 25%.
10-5
м/сек,
т.
е. только на 25%.
Для
фильтров периодического действия в
качестве ориентировочной зависимости
можно принять (при
 и Rфп
= 0)
и Rфп
= 0)
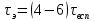 (7)
(7)
где
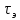 —
экономически оптимальная продолжительность
цикла, сек.
—
экономически оптимальная продолжительность
цикла, сек.
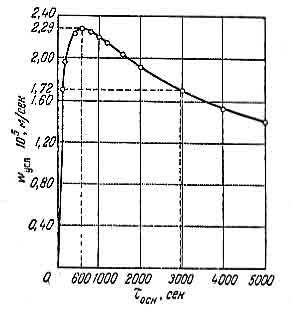
Рис.
1. Зависимость
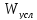 от
от

Определение
постоянных в уравнениях фильтрования.
Под
постоянными в уравнениях фильтрования
понимают отношение объема осадка к
объему фильтрата
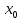 ,
удельное
объемное сопротивление осадка
,
удельное
объемное сопротивление осадка
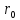 и
сопротивление фильтровальной перегородки
и
сопротивление фильтровальной перегородки
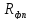 .
Для осадков, встречающихся в химических
производствах и состоящих, как правило,
из частиц размером менее 100 мкм,
эти
величины находят экспериментально.
.
Для осадков, встречающихся в химических
производствах и состоящих, как правило,
из частиц размером менее 100 мкм,
эти
величины находят экспериментально.
Рассмотрим один из способов определения опытным путем указанных величин в уравнении фильтрования при постоянной разности давлений, характеризующийся большой точностью получаемых результатов. Для этого преобразуем упомянутое уравнение к виду
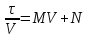 (8)
(8)
где
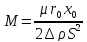 (9)
(9)
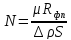 (10)
(10)
При
постоянных температуре и разности
давлений все величины, входящие в правые
части равенств (9) и (10), постоянны. Поэтому
значения М
и
N
также
постоянны, и уравнение (8) является
уравнением прямой линии, наклоненной
к горизонтальной оси под углом, тангенс
которого равен М,
и
отсекающей на оси ординат отрезок N.
Для
построения указанной прямой в координатах
V
–
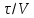 наносят
ряд точек на основании измеренных в
опыте и соответствующих одно другому
значений V
и
наносят
ряд точек на основании измеренных в
опыте и соответствующих одно другому
значений V
и
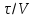 (рис. 2). Затем по графику определяют
величины М
и N, после
чего из равенств (9) и (10) вычисляют
(рис. 2). Затем по графику определяют
величины М
и N, после
чего из равенств (9) и (10) вычисляют
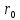 и
и
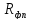 .
Величину
.
Величину
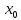 находят в результате непосредственного
измерения объемов осадка и фильтрата.
находят в результате непосредственного
измерения объемов осадка и фильтрата.
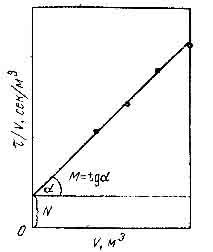
Рис. 2. К определению удельного сопротивления осадка и сопротивления фильтровальной перегородки.
Выполнив серию экспериментов при различных, но постоянных для каждого опыта разностях давлений, можно найти зависимость удельного объемного сопротивления сжимаемого осадка от разности давлений. Установлено, что такая зависимость обычно выражается одним из следующих эмпирических уравнений:
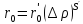 (11)
(11)
или
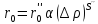 (12)
(12)
где
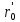 ,
,
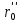 ,
,
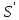 ,
,
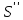 ,
,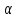 - постоянные, определяемые из опыта.
- постоянные, определяемые из опыта.
Величины
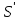 и
и
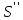 для
встречающихся на практике осадков
обычно находятся в пределах 0—1 хотя
в очень редких случаях они могут быть
больше 1. Эти величины характеризуют
степень сжимаемости осадков и называются
показателями
сжимаемости.
для
встречающихся на практике осадков
обычно находятся в пределах 0—1 хотя
в очень редких случаях они могут быть
больше 1. Эти величины характеризуют
степень сжимаемости осадков и называются
показателями
сжимаемости.
Для относительно крупных частиц, размер которых достаточно велик (порядка 1 мм и более), процессы пептизации и агрегации, а также поверхностные явления не играют существенной роли. В данном случае процесс фильтрования можно рассматривать как гидродинамический процесс течения жидкости сквозь пористую среду.
Учитывая,
что Н
=
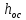 и
и
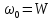 ,
получим
,
получим
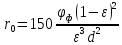 (12а)
(12а)
где
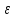 — доля свободного объема, или пористость
слоя;
— доля свободного объема, или пористость
слоя;
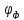 – коэффициент формы; d
- диаметр
шара, имеющего тот же объем, что и частица.
– коэффициент формы; d
- диаметр
шара, имеющего тот же объем, что и частица.
