1- Закон эквивалентов. Химические элементы соединяются друг с другом в строго определенных количествах, соответствующих их эквивалентам. Понятие эквивалента было введено для сопоставления соединительной способности разных элементов. Эквивалентом химического элемента называют такую его массу, которая соединяется с 1,008 ч. м. (части массы) водорода или 8 ч. м. кислорода или замещает эти массы в соединениях. Один и тот же элемент может иметь несколько эквивалентов. Так, эквивалент углерода в оксиде, углерода (IV) равен трем, а в оксиде углерода (II) - шести. Понятие эквивалента можно распространяется и на сложные соединения - основания, кислоты и соли. Эквивалентом сложного соединения называют массу этого соединения, содержащую эквивалент водорода (кислоты) или эквивалент металлической составной части (основания, соли). Формулируется закон так: во всех химических реакциях взаимодействие различных веществ друг с другом происходит в соответствии с их эквивалентами, независимо от того, являются ли эти вещества простыми или сложными.

2 - Закон Авогадро

Авогадро закон, один из основных законов идеальных газов, согласно которому в равных объёмах различных газов при одинаковых температурах и давлениях содержится одинаковое число молекул. Число молекул в одном моле называют Авогадро числом. А. з. открыт А. Авогадро в 1811. Однако из-за господствовавшего в науке 1-й половины 19 в. смешения понятий атома, эквивалента и молекулы А. з. только с 1860 стал широко применяться в физике и химии. Из А. з. следует:

1) 1 кмоль любого идеального газа при одинаковых температурах и давлениях занимает один и тот же объём, равный 22,4136 м³ при давлении 101 325 н/м² (760 мм рт. ст.) и температуре 0°С;

2) плотности r₂ и r₁ двух идеальных газов при одних и тех же давлении и температуре прямо пропорциональны (и удельные объёмы n₁ и n₂ обратно пропорциональны) их молекулярным массам M₂. и M₁ :

3 - Способы определения относительной молекулярной массы веществ

Все синтетические полимерные вещества, независимо от химического способа получения, отличаются полидисперсностью. Рост каждой отдельной молекулы полимера при полимеризации, поликонденсации или в каком-либо другом химическом процессе получения полимеров может прекратиться в любой момент в зависимости от условий проведения данного процесса. Поэтому длина каждой молекулы полимера в конечном продукте химической реакции оказывается произвольной, а образец полимера представляет собой смесь макромолекул различной длины. По этой причине обычно говорят, что полимер обладает полимолекулярностью. Величину каждой молекулы можно характеризовать степенью полимеризации Р, числом элементарных звеньев N в макромолекуле или молекулярной массой М. В случае, когда элементарное звено представляет собой остаток одного мономера, N=Р.

В связи с тем, что любое свойство полимеров обычно определяется, усреднено для всех молекул данного типа, и рассчитанное значение молекулярных характеристик также будет иметь некоторую среднюю величину . Наиболее часто для характеристики макромолекул используют . В зависимости от способа определения средняя молекулярная масса также может различаться. Это связано с тем, что измеренная интенсивность того или иного свойства полимера зависит от длины молекул, их массы или объема. Поэтому существует несколько групп методов, позволяющих определить различные значения молекулярной массы.

Среднечисловая молекулярная масса используется для всех стехиометрических и термодинамических расчетов. Она определяется экспериментальными методами, основанными на измерении интенсивности свойств, связанных с числом молекул. Для определения используются различные методы.

Методы концевых групп.

1). Химические методы, основанные на химическом взаимодействии специально подобранного реагента с химически активными концевыми группами.

2). Спектроскопические методы используются в тех случаях, когда концевые группы имеют оптическую активность.

3). Радиационные методы основаны на определении радиоактивности при введении специальных меток – радиоактивных концевых групп.

Термодинамические методы:

- эбуллиоскопический метод;

- криоскопический метод;

- метод изотермической дистилляции;

- метод определения давления пара над растворами;

- метод осмотического давления.

Все эти методы основаны на определении активности растворенного вещества и крайне чувствительны к присутствию низкомолекулярных фракций и посторонних низкомолекулярных веществ (например, к остаткам катализатора и др.) и, как правило, несколько занижают истинное значение средней молекулярной массы. Кроме того, как методы концевых групп, так и термодинамические методы, исключая метод осмотического давления, ограничены в применении чувствительностью существующих приборов лишь областью молекулярных масс в несколько тысяч единиц. Даже специальные приспособления для высокотемпературной криоскопии и полупроводниковые приборы для определения температуры кипения и замерзания растворов полимеров не позволяют рекомендовать эти методы для определения молекулярной массы свыше 40-50 тыс. Лишь метод осмотического давления позволяет определить среднечисленное значение молекулярной массы полимера в пределах от 10⁴ до 10⁶.

Среднечисленным значением молекулярной массы называют отношение массы полимера к числу молекул в данном образце.

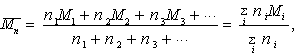(2.5.2)

где n_i= n₁, n₂, n₃...и M_i= M₁, M₂, M₃ - число и молекулярная масса соответствующих фракций молекул.

Весовая доля w_iмолекул с массой M_i может быть выражена как

. (2.5.3)

Если расчет вести на 1 г полимера, т.е. положить, что ,то

, (2.5.4)

откуда

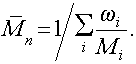(2.5.5)

Поэтому при определении значения среднечисленной массы полимеров концентрацию растворов всегда выражают в г/см³.

Среднемассовая (средневесовая) молекулярная масса представляет собой сумму масс отдельных фракций

. (2.5.6)

C учетом (2.5.3)

. (2.5.7)

Среднемассовая масса полимера определяется методами, чувствительными к массе отдельных молекул. К этим методам можно отнести метод рассеяния, метод диффузии и метод ультраскоростной седиментации (ультрацентрифугирования).

Среднемассовое значение молекулярной массы синтетических полимеров всегда выше среднечисленного значения.

Степень неоднородности (полимолекулярности) полимера определяется по отношению средних значений и как

(2.5.8)

Для мономолекулярного образца полимера или для очень узких фракций , так как .

z - средняя молекулярная масса определяется методом равновесного ультрацентрифугирования, при котором устанавливается равновесие диффузии макромолекул и их седиментации в поле ультрацентрифуги.

Для расчета среднего значения молекулярной массы используется формула

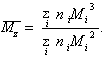(2.5.9)

В общем случае для расчета молекулярной массы можем записать выражение

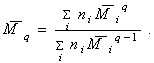(2.5.10)

Величина q может быть как целым числом, так и дробным, чем выше q, лежащее в пределах от 1 до 3, тем более чувствителен метод к присутствию высокомолекулярных фракций и тем выше рассчитанное значение молекулярной массы.

Средневязкостная молекулярная масса рассчитывается из измерений вязкости растворов полимеров по уравнению, которое мы рассмотрели в главе 4 второй части курса , где[h] -характеристическая вязкость, K и а – постоянные, а = 0,5¸1.

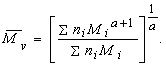(2.5.11)

Обычно отличается от не более чем на 20%, а при а = 1 = .

Метод вискозиметрии основан на определении объема молекул в растворе.

Так как плотность полимера обычно мало отличается от 1 г/см³, то определение позволяет достаточно четко охарактеризовать величину среднемассовой молекулярной массы полимера. Затруднения возникают вследствие изменения формы макромолекул в растворах, что отражает постоянная а.

4 - Понятие внутренней энергии, энтальпии и энтропии системы

Состояние любой системы может быть охарактеризовано значениями непосредственно измеряемых параметров (р, Т и др.). Это характеристика макросостояния системы.  Состояние системы может быть описано также   характеристиками каждой частицы системы (атома, молекулы): координаты, частота колебания, частота вращения и т.д. Это характеристика микросостояния системы.  Системы состоят из очень большого числа частиц, поэтому одному макросостоянию будет отвечать  огромное число различных микросостояний. Это число называется термодинамической вероятностью состояния и обозначается (W).

Термодинамическая вероятность связана с другим свойством вещества – энтропией (S) – формулой Больцмана

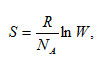       (2.13)

где R - универсальная газовая постоянная, а N_A – постоянная Авогадро. Измеряется энтропия в Дж/(моль^.К).

                Физический смысл: энтропия является мерой неупорядоченности состояния системы. Энтропия системы увеличивается во всех процессах, когда возрастает неупорядоченность (нагревание, растворение, испарение, реакции разложения и т.п.) и уменьшается в процессах, идущих с увеличением упорядоченности (охлаждение, кристаллизация, сжатие и т.п.).

Энтропия является функцией состояния, но в отличие от большинства других термодинамических функций возможно экспериментальное определение абсолютного значения энтропии вещества. Эта возможность основана на постулате М.Планка, согласно которому «при абсолютном нуле энтропия идеального кристалла равна нулю» (третий закон термодинамики).

Температурная зависимость энтропии вещества представлена качественно на рис.2.1.

     

 

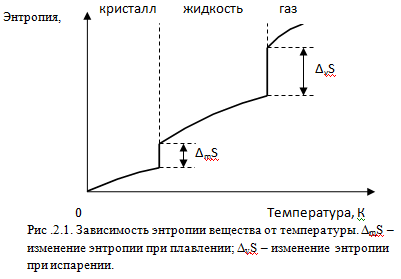
   На рис.2.1 видно, что при нуле Кельвина энтропия вещества равна нулю. При повышении температуры энтропия плавно увеличивается, а в точках фазовых переходов   имеет место скачкообразное увеличение энтропии, определяемое соотношением

                                                        (2.14)

где Δ _ф..п.S, Δ_ф.п.Н и  Т_ф.п. изменение энтропии, энтальпии и температура фазового перехода, соответственно.

Энтропию вещества B в стандартном состоянии обозначают  . Для многих веществ абсолютные значения стандартных энтропий определены и приводятся в справочных изданиях.

Энтропия, также как внутренняя энергия и энтальпия, является функцией состояния, поэтому изменение энтропии системы в процессе не зависит от его пути и определяется только начальным и конечным состоянием системы. Изменение энтропии в ходе химической реакции (2.10) может быть найдено, как разность суммы энтропий продуктов реакции и суммы энтропий исходных веществ

  

Понятие энтропии используется в одной из формулировок второго закона термодинамики:  в изолированных системах могут самопроизвольно протекать только  процессы, идущие с увеличением энтропии (ΔS>0).  Под изолированными системами понимаются системы, не обменивающиеся с окружающей средой ни веществом, ни энергией. Системы, в которых протекают химические процессы, к изолированным системам не относятся, т.к. они обмениваются с окружающей средой энергией (тепловой эффект реакции).

 1-й закон термодинамики, внутренняя энергия, тепло, работа, энтальпия, энтропия.

Первый закон термодинамики гласит, (4 разные формулировки) что :

• Энергия не может быть создана или уничтожена (закон сохранения энергии), она лишь переходит из одного вида в другой в различных физических процессах. Отсюда следует, что внутренняя энергия изолированной системы остается неизменной.

• Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы против внешних сил.

• Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданной системе и не зависит от способа, которым осуществляется этот переход.

• Изменение внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты, переданной системе, и работой, совершенной системой над внешними силами.

Первый закон термодинами гласит, что энергия не может быть создана или уничтожена. Таким образом, энергия системы (замкнутой) - постоянна. Тем не менее, энергия может быть передана от одного элемента системы другому. Рассмотрим замкнутую систему, изолированную от остальных.

Передача энергии между различными подсистемами в ней может быть описана как :

E₁ = E₂        

где

E₁ = начальная энергия

E₂ = конечная энергия

Внутрення энергия включает :

• Кинетическую энергию движения атомов

• Потенциальную энергию хранящуюся в химических связях

• Гравитационную энергию системы

Первый закон является основой для термодинамической науки и инженерного анализа.

Базируется на возможных типах обмена (энергии), ниже приведены 3 типа систем:

• пред - изолированные системы (isolated systems): отсутствует обмен элементами системы или энергией

• закрытые системы (closed systems): отсутствует обмен элементами системы, но присутствует некоторый обмен энергией

• открытые системы (open systems): возможен обмен как элементами системы, так и энергией

Первый закон термодинамики помогает использовать ключевые концепции внутренней энергии (internal energy), тепла (heat), и работы системы (system work). которые широко используются в описании тепловых систем (heat engines).

• Внутренняя энергия ( Internal Energy) - Внутренняя энергия определяется как энергия случайных, находящихся в неупорядченном движении молекул. Энергия молекул находится в диапазоне от высокой, необходимой для движения, до заметной лишь с помощью микроскопа энергии на молекулярном или атомном уровне. Например, у стакана с водой комнатной температы, стоящего на столе нет, на первый взгляд, никакой энергии: ни кинетической, ни потенциальной относительно стола. Но, с помощью микроскопа становится заметна "бурлящая" масса быстро двигающихся молекул. Если выплеснуть воду из стакана, эта микроскопическая энергия не обязательно заметно изменится, когда мы усредним добавленную кинетическую энергию на все молекулы воды.

• Тепло - Тепло может быть определено, как энергия, передаваемая от объекта с более высокой температурой к объекту с менее высокой температурой. Сам по себе объект не обладает "теплом"; соответствующий термин для микроскопической энергии объекта - внутренняя энергия. Внутренняя энергия может увеличиваться путем переноса энергии к объекту от объекта, имеющего температуру выше - этот процесс называется нагревом.

• Работа - Когда работа совершается термодинамической системой (чаще всего это газ, который совершает работу), то работа совершенная газом при постоянном давлении определяется как : W = p dV, где W - работа, p - давление, а dV -изменение объема. В случаях когда давление не является постоянным, работа может быть представлена интегральным образом, как площадь поверхности под кривой в координатах давление, объем, которые представляют происходящий процесс.

Изменение внутренней энергии системы равно теплу (добавленному системе) минус работа, совершенная системой

dE = Q - W        

где

dE = изменение внутренней энергии

Q = добавленное тепло

W =работа системы

1й закон не дает информации о характере процесса и не определяет конечного состояния равновесия. Интуитивно мы понимаем, что энергия переходит от объекта с более высокой температурой к объекту с менее высокой температурой. Таким образом, 2й закон нам нужен для получения информации о характере процесса.

Энтальпия -

• это "термодинамический потенциал " используемый в химической термодинамике реакций и не циклических процессов.

• однозначная функция состояния термодинамической системы при независимых параметрах энтропии и давления, связана с внутренней энергией соотношением, приведенным ниже.

• это свойство вещества, указывающее количество энергии, которую можно преобразовать в теплоту.

Энтальпия определяется как:

H = U + PV        

где

H = энтальпия

U = внутренняя энергия

P = давление

V = объем системы

При постоянном давлении изменение энтальпии равно количеству теплоты, подведенной к системе, поэтому энтальпию часто называют тепловой функцией или теплосодержанием. В состоянии термодинамического равновесия энтальпия системы минимальна.

Энтальпия является точно измеряемым параметром, когда определены способы выражения трех других поддающихся точному определению параметров формулы выше.

Энтропия.

Термин "энтропия" - величина, характеризующая степень неопределенности системы.

Однако, в термодинамике это понятие используется для определения связанной энергии системы. Энтропия определяет способность одной системы влиять на другую. Когда объекты пересекают нижнюю границу энергетического уровня необходимого для воздействия на окружающую среду, энтропия возрастает.Энтропия связана со вторым законом термодинамики.

Энтропия (обычно обозначается S), функция состояния термодинамической системы, изменение которой dS в равновесном процессе равно отношению количества теплоты dQ, сообщенного системе или отведенного от нее, к термодинамической температуре Т системы.

в символьном виде записывается, как

dS=(dQ)/T

где

dS - изменение термодинамической системы

dQ - количество теплоты, сообщенное системе

T - термодинамическая температура системы

 

Неравновесные процессы в изолированной системе сопровождаются ростом энтропии, они приближают систему к состоянию равновесия, в котором S максимальна (закон неубывания энтропии).

Для вселенной в целом энтропия возрастает.

5 - Закон Гесса

Гесса закон

• Закон Гесса (схема)

Закон Гесса (схема)

Гесса закон, основной закон термохимии, согласно которому тепловой эффект реакции зависит лишь от начального и конечного состояний системы и не зависит от промежуточных состояний и путей перехода. Г. з. был открыт Г. И. Гессом в 1840 на основе экспериментальных исследований. Он представляет собой одну из форм позднее открытого закона сохранения энергии в применении его к химическим реакциям и относится к процессам, происходящим при постоянном объёме или при постоянном давлении. Г. з. широко используется для определения расчётным путём теплового эффекта интересующего процесса на основе экспериментальных данных, относящихся к др. процессам (в т. ч. даже к процессам, практически недоступным в данных условиях). Так, для 298,15 К теплоту образования окиси углерода ( ккал/моль) из графита можно рассчитать, зная, что теплоты сгорания  окиси углерода и графита до CO₂ при этой температуре равны соответственно —282,99 и —393,32 кдж/моль (—67,635 и—94,051 ккал/моль). 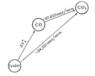Рассматривая два пути образования CO₂ из графита при непосредственном сжигании его до CO₂ и при промежуточном образовании СО (см. рис.) и зная, что по Г. з. общий тепловой эффект обоих путей перехода должен быть одинаковым, находим  ккал/моль (теплота выделяется).

6 - Энергия активации реакции

Энергия активации, разность между значениями средней энергии частиц (молекул, радикалов, ионов и др.), вступающих в элементарный акт химической реакции, и средней энергии всех частиц, находящихся в реагирующей системе. Для различных химических реакций Энергия активации изменяется в широких пределах - от нескольких до ~ 10 дж./ моль. Для одной и той же химической реакции значение Энергия активации зависит от вида функций распределения молекул по энергиям их поступательного движения и внутренним степеням свободы (электронным, колебательным, вращательным). Как статистическую величину Энергия активации следует отличать от пороговой энергии, или энергетического барьера, - минимальной энергии, которой должна обладать одна пара сталкивающихся частиц для протекания данной элементарной реакции.   В рамках представлений теории абсолютных скоростей реакций Энергия активации - разность между значениями средней энергии активированных комплексов и средней энергии исходных молекул.   Представления об Энергия активации возникли в 70-80-х гг. 19 в. в результате работ Я. Вант-Гоффа и С. Аррениуса, посвященных изучению влияния температуры на скорость химической реакции. Константа скорости реакции k связана с Энергия активации (Е) уравнением Аррениуса:   k = k_oe^-E/RT   где R - газовая постоянная, Т - абсолютная температура в К, k_o - постоянная, называемая предэкспоненциальным множителем константы скорости. Это уравнение, основанное на молекулярно-кинетической теории, позже было получено в статистической физике с учетом ряда упрощающих предположений, одно из которых - независимость Энергия активации от температуры. Для практики и для теоретических расчетов в сравнительно узких температурных интервалах это предположение справедливо.   Энергия активации можно найти по экспериментальным данным несколькими способами. Согласно одному из них, исследуют кинетику реакции при нескольких температурах (о методах см. в ст. Скорость химической реакции) и строят график в координатах In k - 1/T; тангенс угла наклона прямой на этом графике, в соответствии с уравнением Аррениуса, равен Е. Для одностадийных обратимых реакций (см. Обратимые и необратимые реакции) Э. а. реакции в одном из направлений (прямом или обратном) можно вычислить, если известна Энергия активации реакции в другом и температурная зависимость константы равновесия (из термодинамических данных). Для более точных расчетов следует учитывать зависимость Энергия активации от температуры.   Энергия активации сложных реакций представляет собой комбинацию Энергия активации элементарных стадий. Иногда, помимо истинной Энергия активации, определяемой по уравнению Аррениуса, используют понятие «кажущейся» Энергия активации Например, если константы скоростей гетерогенно-каталитических реакций определяют по изменению объемных концентраций исходных веществ и продуктов, то кажущаяся Энергия активации отличается от истинной на величину тепловых эффектов, сопровождающих процессы адсорбции и десорбции реагирующих веществ на поверхности катализатора. В неравновесных системах, например плазмохимических (см. Плазмохимия), определение Энергия активации является очень сложной задачей. В некоторых случаях, однако, возможно формальное применение уравнения Аррениуса.   Энергия активации - важнейшее понятие кинетики химической; ее значения включают в специальные справочники и используют в химической технологии для расчета скоростей реакций в различных условиях.

7 - Зависимость скорости химической реакции от концентрации реагирующих веществ и температуры.

1. Влияние температуры на скорость химических процессов. Правило Вант-Гоффа

Скорость химической реакции - это величина, показывающая как изменяются концентрации исходных веществ или продуктов реакции за единицу времени.

Скорость химической реакции зависит от природы реагирующих веществ и условий протекания реакции: концентрации с, температуры t, присутствия катализаторов, а также от некоторых других факторов (например, от давления - для газовых реакций, от измельчения - для твердых веществ, от радиоактивного облучения).

Влияние концентраций реагирующих веществ. Чтобы осуществля¬лось химическое взаимодействие веществ А и В, их молекулы (частицы) должны столкнуться. Чем больше столкновений, тем быстрее протекает реакция. Число же столкновений тем больше, чем выше концентрация реагирующих веществ. Отсюда на основе обширного экспериментального материала сформулирован основной закон химической кинетики, устанавливающий зависимость скорости реакции от концентрации реагирующих веществ:

Скорость химической реакции пропорциональна произведению концентраций реагирующих веществ.

Для реакции (I) этот закон выразится уравнением

v = kc_A c_B, (1)

где сА и сВ - концентрации веществ А и В, моль/л; k - коэффициент пропорциональности, называемый константой скорости реакции. Основной закон химической кинетики часто называют законом действующих масс.

Из уравнения (1) нетрудно установить физический смысл константы скорости k: она численно равна скорости реакции, когда концентрации каждого из реагирующих веществ составляют 1 моль/л или когда их произведение равно единице.

Константа скорости реакции k зависит от природы реагирующих веществ и от температуры, но не зависит от их концентраций.

Уравнение (1), связывающее скорость реакции с концентрацией реагирующих веществ, называется кинетическим уравнением реакции. Если опытным путем определено кинетическое уравнение реакции, то с его помощью можно вычислять скорости при других концентрациях тех же реагирующих веществ.

Зависимость скорости реакции от температуры определяется правилом Вант-Гоффа:

При повышении температуры на каждые 10о скорость большинства реакций увеличивается в 2-4 раза.

Математически эта зависимость выражается соотношением

v_{t 2} = v_{t 1} г,

где vt 1, vt 2 - скорости реакции соответственно при начальной (t 1) и конечной (t 2) температурах, а г - температурный коэффициент скорости реакции, который показывает, во сколько раз увеличивается скорость реакции с повышением температуры реагирующих веществ на 10°.

Правило Вант-Гоффа является приближенным и применимо лишь для ориентировочной оценки влияния температуры на скорость реакции. Температура влияет на скорость химической реакции, увеличивая константу скорости.

Вычислите, во сколько раз уменьшится скорость реакции, протекающей в газовой фазе, если понизить температуру от 120є до 60єС. Температурный коэффициент равен 3.

Ответ. Скорость химической реакции при понижении температуры от 120є до 60є С уменьшится в 729 раз.

2. Второй закон термодинамики. Самопроизвольные процессы. Свободная и связанная энергия. Энтропия

Химическая термодинамика - наука, изучающая условия устойчивости систем и законы.

Термодинамика - наука о макросистемах (рис.1).

Рисунок 1. Схема составляющих термодинамической науки

Первое начало термодинамики утверждает, что при превращении одной формы энергии в другую полная энергия системы не изменяется, однако не указывает никаких ограничений относительно возможности этого процесса. Поэтому первое начало термодинамики позволяет рассчитать энергетический эффект процесса, однако не дает ответа на вопросы о том, будет ли процесс протекать самопроизвольно, о направлении и глубине протекания процесса.

Самопроизвольный процесс - процесс, который может протекать без затраты работы извне, причем в результате может быть получена работа в количестве, пропорциональном произошедшему изменению состояния системы. Самопроизвольный процесс может протекать или обратимо, или необратимо. Чтобы самопроизвольный процесс протекал обратимо, необходимо приложить извне такое сопротивление, чтобы переход был очень медленным и при бесконечно малом изменении противодействующей силы процесс мог пойти в обратном направлении. В случае обратимо происходящего изменения состояния системы производится максимальное количество работы. Всякий реальный процесс в какой-то степени является необратимым, и получаемая работа меньше максимально возможного теоретического количества.

Вынужденный процесс - процесс, для протекания которого требуется затрата работы извне в количестве, пропорциональном производимому изменению состояния системы.

Второе начало термодинамики дает возможность определить, какой из процессов будет протекать самопроизвольно, какое количество работы может быть при этом получено, каков предел самопроизвольного течения процесса. Далее, второе начало термодинамики дает возможность определить, какими должны быть условия, чтобы нужный процесс протекал в необходимом направлении и в требуемой степени, что особенно важно для решения различных задач прикладного характера.

Естественные процессы всегда направлены в сторону достижения оси с темой равновесного состояния (механического, термического или любого другого). Это явление отражено вторым законом термодинамики, имеющим большое значение и для анализа работы теплоэнергетических машин. В соответствии с этим законом, например, теплота самопроизвольно может переходить только от тела с большей температурой к телу с меньшей температурой. Для осуществления обратного процесса должна быть затрачена определенная работа. В связи с этим второй закон термодинамики можно сформулировать следующим образом: невозможен процесс, при котором теплота переходила бы самопроизвольно от тел более холодных к телам более теплым (постулат Клаузиуса, 1850 г.).

Любая форма энергии может полностью перейти в теплоту, но теплота преобразуется в другие формы энергии лишь частично.

химический термодинамика скорость раствор

Таким образом, можно условно принять, что внутренняя энергии системы состоит из двух составляющих: "свободной" X и "связанной" Y энергий, причем "свободная" энергия может быть переведена в работу, а "связанная" энергия может перейти только в теплоту.

Мерой связанной энергии является новая термодинамическая функция состояния, называемая энтропией.

В природе протекание большинства процессов, в том числе и химических, сопровождается не только энергетическими эффектами, но и изменением в упорядочении расположения частиц относительно друг друга. Рассмотренные выше примеры превращений имеют одно общее свойство: в каждом случае состояние продуктов характеризуется большей хаотичностью, или неупорядоченностью, чем состояние реагентов. Растворение хлорида калия сопровождается нарушением регулярности в расположении частиц в узлах кристаллической решетки - возникает беспорядочное распределение ионов в растворе. Молекулы воды, образующие кристалл льда, прочно удерживаются в его кристаллической решетке. При плавлении льда молекулы H2O начинают свободно перемещаться относительно друг друга. Высокоупорядоченная кристаллическая структура заменяется неупорядоченной структурой жидкости. В процессе испарения структура жидкости, представленная ассоциатами из ее молекул, заменяется отдельными молекулами, движущимися независимо (в газовой фазе).

Таким образом, частицам (молекулам, атомам, ионам и др.) присуще стремление к беспорядочному движению, поэтому система стремится перейти из более упорядоченного состояния в менее упорядоченное. Количественной мерой неупорядоченности (беспорядка) системы является термодинамическая функция состояния системы - энтропия (S, Дж/ (мольK)). Чем в большей мере выражен беспорядок в системе, тем больше ее энтропия. Следовательно, еще одной составляющей движущей силы самопроизвольно протекающих процессов является тенденция к увеличению энтропии системы.

II закон термодинамики является одним из наиболее общих положений всей науки в целом. Главная мысль его заключается в том, что в любой изолированной системе с течением времени происходит постоянное возрастание степени беспорядка, т.е. энтропии. Следовательно, для любых самопроизвольных процессов

ДS ? 0.

Знак ">" - для необратимых процессов, знак "=" - для обратимых процессов.

Для обратимых процессов ДS = Q/T, [Дж/К моль].

Для необратимых процессов ДS > Q/T, [Дж/К моль].

II закон термодинамики имеет ясный физический смысл только тогда, когда его применяют к любой ограниченной системе. Функции системы, которые связаны с работой и говорящие о направлении процесса, называются термодинамическими потенциалами. Критерием для суждения о направлении процессов в изолированных системах может служить изменение энтропии ДS. Однако на практике большинство процессов протекает в неизолированных системах и связано с теплообменом и изменением объема. Поэтому для неизолированных систем необходимо иметь другие критерии. Энтропию веществ принято относить к стандартным условиям (T = 298,15 K и p = 101,3 кПа). Энтропию при этих условиях называют стандартной энтропией и обозначают S° (298 K). Значения стандартных энтропий для многих веществ являются справочными данными.