Примеры задач линейного программирования.

1. Задача об использовании ресурсов (планирования производства).

Для изготовления двух видов продукции диетического питания Р₁ и Р₂ используют четыре вида ресурсов S₁, S₂, S₃, S₄. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 1.

Таблица 1.

Вид ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление единицы продукции
		P1	P2
S1	18	1	3
S2	16	2	1
S3	5	—	1
S4	21	3	—

Прибыль, получаемая от реализации единиц продукции диетического питания Р₁ и Р₂ – соответственно 2 и 3 рубля.

Необходимо составить такой план производства продуктов диетического питания, при котором прибыль от ее реализации будет максимальной.

Решение.

Составим математическую модель задачи. Обозначим Х₁ и Х₂ – число единиц продукции соответственно Р₁ и Р₂, запланированных к производству. Для их изготовления, согласно таблицы 1, потребуется (1х₁ + 3х₂) единиц ресурса S₁, (2х₁ + 1х₂) единиц ресурса S₂, (1х₂)единиц ресурса S₃ и 3х₁, единиц ресурса S₄.

Т.к. потребление ресурсов S₁, S₂, S₃, S₄ не должно превышать их запасов, соответственно 18, 16, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выражается системой неравенств:

х₁ + 3 х₂ ≤ 18;

2х₁ + х₂ ≤ 16; (1)

х₂ ≤ 5;

3х₁ ≤ 21.

По смыслу задачи переменные

х₁ ≤ 0; х₂ ≥0. (2)

Суммарная прибыль F составит 2х₁, от реализации продукции Р₁ и 3х₂ – от реализации продукции Р₂, т.к.

F = 2х₁ + 3х₂ (3)

Итак, экономико-математическая модель задачи: найти такой ??? выпуска продукции Х = (х₁, х₂), удовлетворяющий системе (1), условию (2), при котором (3) примет максимальное значение.

Задачу можно обобщить на случай выпуска "n" видов диетпродуктов с использованием "m" видов ресурсов. Обозначим х_j (j = 1, 2, 3, …, n) – число единиц диет продукции Р_j запланированной к производству; b_i (i = 1, 2, 3, …, m) – запасы ресурса S_i; a_ij – число единиц ресурса S_i, затрачиваемое на изготовление единицы продукции P_j (a_ij – технологические конфликты); С_j – прибыль от реализации единицы продукции Р_j. Тогда экономико-математическая модель задачи об использовании ресурсов в общей постановке примет вид: найти такой план Х = (х₁, х₂, …,х_n) выпуска продукции, удовлетворяющий системе

а₁₁х₁ + а₁₂х₂ + … + а_1nх_n ≤ b₁,

а₂₁х₁ + а₂₂х₂ + … + а_2nх_n ≤ b₂,

…………………………….. (4)

а_m1х₁ + а_m2х₂ + … + а_mnх_n ≤ b_m

и условию

х₁ ≥ 0, х₂ ≥ 0, …, х_n ≥ 0, (5)

при котором функция

F = с₁х₁ + с₂х₂ + … + с_nх_n (6)

примет максимальное значение.

2. Задача об оптимальной рецептуре детского питания.

Имеется два вида детского питания I и II, содержащее витамины S₁; S₂; S₃. Содержание числа единиц витаминов в 1 кг каждого вида детского питания и необходимый минимум витаминов приведены в таблице 2 (цифры условные).

Стоимость 1 кг детского питания I и II соответственно равна 4 и 6 руб.

Необходимо составить оптимальную рецептуру указанных видов детского питания, имеющих минимальную стоимость, в которой содержание каждого вида витаминов было бы не менее установленного предела.

Решение.

Составим экономико-математическую модель задачи.

Обозначим х₁ и х₂ – количество продуктов I и II, входящих в дневной рацион детского питания. Этот рацион будет включать (3х₁ + 1х₂) единиц витамина S₁; (1х₁ + 2х₂) единиц витамина S₂; (1х₁ + 6х₂) единиц витамина S₃. Так как содержание витаминов S₁; S₂; S₃ в рационе должно быть не менее соответственно 9, 8, 12 единиц, то получим систему неравенств:

3х₁ + х₂ ≥ 9;

х₁ + 2х₂ ≥ 8; (7)

х₁ + 6х₂ ≥ 12.

Кроме того, переменные

х₁ ≥ 0, х₂ ≥ 0 (8)

Общая стоимость рациона составит (в руб.)

F = 4х₁ + 6х₂ (9)

Итак, экономико-математическая модель задачи: составить рецептуру дневного рациона детского питания Х = (х₁, х₂), удовлетворяющий системе (7) и условию (8), при котором функция (9) принимает максимальное значение.

Для формализации задачи в общей постановке обозначим: х_j (j = 1, 2, …, n) – число единиц детского питания "n-го" вида; b_i (i = 1, 2, 3, …, m), - необходимый минимум содержание в рецептуре питания витаминов S_i; a_ij – число единиц витаминов S_i в единице детского питания j-го вида; с_j – стоимость единицы детского питания j-го вида. Тогда экономико-математическая модель задачи примет вид: найти такую рецептуру рациона детского питания Х = (х₁, х₂, …х_n), удовлетворяющую системе

а₁₁х₁ + а₁₂х₂ + … + а_1nх_n ≥ b₁,

а₂₁х₁ + а₂₂х₂ + … + а_2nх_n ≥ b₂,

…………………………….. (10)

а_m1х₁ + а_m2х₂ + … + а_mnх_n ≥ b_m

и условию

х₁ ≥ 0, х₂ ≥ 0, …, х_n ≥ 0, (11)

при котором функция

F = с₁х₁ + с₂х₂ + … + с_nх_n (12)

принимает максимальное значение.

6.2.7.5. Модели нелинейного программирования.

Ниже в краткой форме представлены материалы:

1. классические методы определения экстремумов:

2. методы выпуклого программирования;

3. модели динамического программирования.

А. Классические методы определения экстремумов.

Во многих задачах исследования операций зависимость между показателями (постепенными, переменными) являются нелинейными. В этих случаях возникают задачи нелинейного программирования. Можно выделить класс нелинейных задач, которые относятся к классическим методам оптимизации.

Допустим, что среди ограничений решения задачи нет неравенств, необязательны условия неотрицательности, переменные не являются дискретными, m < n, а функции φ_i (х) и f (х) непрерывны и имеют частные производные по крайней мере второго порядка. В этом случае, задачу оптимизации можно сформулировать так: найти переменные х₁, х₂, …х_n удовлетворяющие системе уравнений

φ_i (х₁, х₂, …х_n) = b_i, i = 1, 2, …, m (1)

и образующая в максимум (минимум) целевую функцию

Z = f (х₁, х₂, …х_n) (2)

Такие задачи можно решать классическими методами дифференцированного исчисления. При этом классические методы часто используются не в качестве вычислительного средства, а как основа для теоретического анализа.

Примером простой нелинейной задачи является следующая:

Пищевое предприятие для производства какого-то продукта использует два вида средств х₁ и х₂. Например: технологические аппараты и труд (факторы производства), а х₁ и х₂ затраты факторов производства. Величина затрат: работы ТА (машин) в соответствии с человеческим трудом могут быть больше или меньше. Это определяет производство как более или менее трудоемкое. Объем производства пищевых продуктов (выраженных в натуральных или стоимостных единицах) является функцией затрат производства Z = f (х₁, х₂). Эта зависимость называется производственной функцией. Издержки зависят от расхода х₁ и х₂ и от цен этих факторов (с₁ и с₂). Совокупные издержки выражаются формулой b = с₁х₁ + с₂х₂.

Требуется при данных совокупных издержках определить такое количество факторов производства, которые максимизирует объем продукции Z.

Математическая модель задачи имеет вид: определить такие величины переменных х₁ и х₂, которые бы удовлетворяли условиям

с₁х₁ + с₂х₂ = b; (3)

х₁ ≥ 0, х₂ ≥ 0,

при которых функция

Z = f (х₁, х₂) (4)

достигает максимума.

Как правило, функция (4) может иметь произвольный нелинейный вид.

Примечание: будем ???, что функция Z = f (х₁, х₂, …х_n) = f (х) дважды дифференцируема в тоже , и в некоторой ее окрестности. Если для всех точек х этой окрестности f (x^*) ≥ f (x), или f (x^*) ≤ f (x), то говорят, что функция f (x) имеет экстремум х^* (максимум или минимум). Точка х^*, в которой все частные производные функции Z = f (х) равны "0", называются стационарной точкой.

Необходимое условие экстремума.

Если в точке х^* функция Z = f (х) имеет экстремум, то частные производные функции в этой точке равны нулю:

, i = 1, 2, …, n.

Следовательно, точки экстремума функции Z = f (х) удовлетворяют системе уравнений:

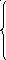
(5)

Необходимое условие (как и для случая ??? переменной) не является достаточным для того, чтобы стационарная точка была точкой экстремума. Для получения достаточного условия следует определить в стационарной точке знак дифференциала второго порядка. Дифференциал второго порядка равен сумме произведений частных производных второго порядка на соответствующие приращения аргументов.

Если от частной производной найти частную производную по переменной х_j, то получим частную производную второго порядка по переменным х_i, х_j, которая обозначается как в этом случае:

Итак, достаточное условие экстремума:

1. в стационарной точке Х⁰ функция Z = f (х) имеет максимум, если d² f (x⁰) < 0, минимум, если d² f (x⁰) > 0, при любых Δх_i и Δх_j (в этих случаях Х⁰ = Х*), не обращаются в нуль одновременно.

2. если d² f (x⁰) может принимать в зависимости от Δх_i и Δх_j и положительные, и отрицательные значения, то в точке х⁰ экстремума нет.

Для функции двух переменных (производственной), когда Z = f (х₁, х₂) достаточные условия просты. Существует четыре частные производные второго порядка:

Из них две смешанные производные и , если являются непрерывными, то равны. Найдем значение частных производных второго порядка в стационарной точке :

; ; ; (можно убедиться, что а₁₂ = а₂₁). Обозначим через Δ определитель, составленный из а_ij для i, j = 1,2:

.

Тогда достаточные условия экстремума функции двух переменных имеют вид:

1. если Δ > 0 и а₁₁ < 0, (а₂₂ < 0), то в точке х⁰ функция имеет максимум; если Δ > 0 и а₁₁ > 0, (а₂₂ > 0), то в точке х⁰ – минимум (в этом случае х⁰ = х*);

2. если Δ < 0, то экстремума нет;

3. если Δ = 0, то вопрос об экстремуме открыт.

Пример.

Исследовать на экстремум функцию:

.

Решение. Находим частные производные:

(6)

приравниваем их нулю:

(7)

решаем систему уравнений (7). Вычитаем из первого уравнение второе: , поэтому х₁ = х₂, тогда , откуда х₁ = 0; или . Т.о. имеем три стационарные точки х¹ = (0;0); х² = (1;1); х³ = (-1; -1).

Найдем вторые частные производные, используя уравнение (6):

Вычислим значения вторых частных производных в каждой стационарной точке, составим определитель Δ и применим достаточные условия экстремума:

В точке Х' = (0; 0); а₁₁ = -2; а₁₂ = а₂₁ = -2; а₂₂ = -2;

Вопрос об экстремуме остался открытым, (такая точка называется седловой).

В точке Х² = (1, 1), в точке Х³ = (-1, -1):

а₁₁ = 10; а₁₂ = а₂₁ = -2; а₂₂ = 10; .

Функция в этих точках имеет минимум, так как Δ > 0, а₁₁ > 0, Z_min = -2.

Ф

Если область D замкнута и ограничена, то дифференцируемая функция Z = f (x) достигает в этой области своих наибольшего и наименьшего значений в стационарной точке, или в граничной точке области (теорема Вейерштрасса).

ункция Z = f (x) имеет в точке Х⁰ заданной области D глобальный максимум или глобальный минимум, если неравенство f (x) ≤ f (x⁰) или f (x) ≥ f (x⁰) соответственно выполняется для любой точке .

Б. Метод множителей Лагранжа.

Этот способ определения условного экстремума заключается в построении вспомогательной функции Лагранжа¹, которая в области допустимых достигает максимума для тех же значений переменных х₁, х₂, …, х_n, что и целевая функция Z.

Пусть решается задача определения условного экстремума функции Z = f (x) при ограничении

φ_i (х₁, х₂, х₃, …, х_n) = 0; i =1, 2, 3, …, m, m < n.

составим функцию

(1 – 5)

которая называется функцией Лагранжа. Множителям Лагранжа можно придать экономический смысл. Если f (х₁, х₂, …, х_n) – доход, соответствующий плану х = (х₁, х₂, х₃, …, х_n), и функция φ_i (х₁, х₂, …, х_n) – издержки i-го ресурса, соответствующие этому плану, то λ_i – цена (оценка) i-го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения размера i-го ресурса (??? оценка).

L (х) – функция n + m переменных (х₁, х₂, х₃, …, х_n, λ₁, λ₂, …, λ_m).

Определение стационарных точек этой функции приводит к решению системы уравнений:

(2)

в уравнения (2) входят уравнения связи:

Таким образом, задача нахождения условного экстремума функции Z = f (x) сводится к нахождению локального экстремума функции L (х). Если стационарная точка найдена, то существование экстремума определяется исследованием знака второго дифференциала d² L (х) в стационарной точке при условии, что переменные приращения Δx_j связаны соотношениями

i = 1, 2, 3, …, m (3)

полученными путем дифференцирования уравнений связи.

____________________________

¹ Ж.Л. Лагранжа (1736 – 1813) – французский математик.

Пример.

Найти наибольшее и наименьшее значения функции при условии, что х₁, х₂, х₃ удовлетворяют уравнению .

Решение.

Уравнение связи определяет в пространстве сферу единично радиуса с центром в начале координат (рис. 1 – 5).

Так как сфера – замкнутое ограниченное множество, то согласно теореме Вейерштрасса функция достигает на ней своего наибольшего и наименьшего значений.

Необходимо найти условный глобальный экстремум. Запишем уравнение связи в виде: . Составим функцию Лагранжа:

Найдем частные производные этой функции по х₁, х₂, х₃, λ.

Приравняв частные производные к нулю, получим систему:

Решая систему, получим стационарные точки, в которых найдем значения функции Z:

1. х₁ = х₂ = 0; х₃ = ± 1 => Z = 0.

2. х₁ = 0; х₂ = ± 1; х₃ = 0 => Z = 0.

3. х₁ = ± 1; х₂ = х₃ = 0 => Z = 0.

4. х₁ = 0; х₂ = х₃ = => Z = .

5. ; х₂ = 0; х₃ = => Z = 1.

6. х₁ = х₂ = 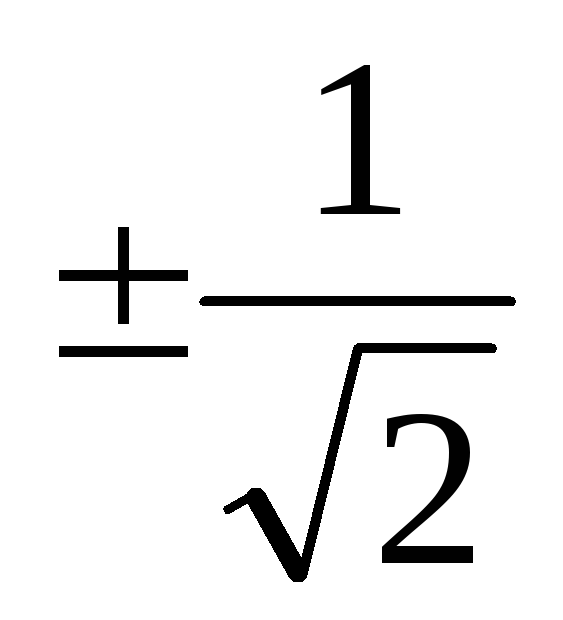; х₃ = 0 => Z = .

Выберем из всех значений Z наибольшее и наименьшее: Z_наиб. = 1, а Z_наим. = 0. Легко видеть в каких точках сферы достигаются эти значения.

Если число переменных n = 2, нелинейные задачи можно решать геометрически. Ограничения должны быть записаны в виде неравенств.

φ_i (х₁, х₂) ≤ b_i, i = 1, 2, …, m (4)

а целевая функция должна иметь вид:

Z = f (х₁, х₂) (5)

В. Модели выпуклого программирования.

Рассмотрим задачу нелинейного программирования при условии, что функции f и φ_i, (i = 1, 2, …, m) являются выпуклыми. Введем необходимые понятия.

Производной функции F (x) = F (x₁, x₂, …, x_n) по направлению "l" в точке х называется предел

.

Направление "l" обычно задается вектором l = (l₁, …, l_n). Если функция F дифференцируема в точке Х, то она имеет в этой точке производную по любому направлению l, которая выражается через частные производные по формуле

(6)

где | l | - длина вектора "l", т.е. .

Абсолютная величина производной по направлению дает скорость изменения функции в этом направлении, а знак показывает характер изменении функции (возрастание или убывание).

Градиентом функции F (x) = F (x₁, x₂, …, x_n) называется вектор, проекциями которого на координатные оси служат соответствующие частные производные, т.е.

.

достигается тогда, когда направление "l" совпадает с направлением равна:

.

Таким образом, в каждой точке Х направление градиента является направлением наибольшего возрастания функции, а длина градиента равна наибольшей скорости возрастания функции в этой точке.

Пример.

Найти наибольшую скорость возрастания функции F = х₁х₂х₃ + 2х₃ в точке А (0; 1; 2) и определить характер изменения этой функции в точке А в направлении l = (1; -2; 2).

Решение.

Так как , то и (2, 0, 2). Т.о., наибольшая скорость возрастания функции в точке А равна . Далее . И Так как , то функция F в точке А в направлении "l" возрастает.

Г. Приближенное решение задач выпуклого программирования градиентным методом, (метод спуска).

Общая схема решения задач математического программирования методами спуска состоит в построении последовательности

Х₀, Х₁, Х₂, …, Х_k (1)

решений системы ограничений данной задачи по следующему принципу: в качестве Х₀ выбирается любая точка области решений и затем каждая последующая точка получается из предыдущей по формуле:

(2)

где - некоторое направление, т.е. вектор, а λ – число. При этом направление "l" и длина шага "λ" выбираются так, чтобы обеспечить сходимость последовательности (1) к оптимальному решению Х*. В общем случае процесс получения последовательных приближений Х_k бесконечен (и тогда некоторое берется за приближенное значение оптимального решения Х*). Однако иногда процесс завершается за конечное число шагов, приводя к локальному, а в задачах выпуклого программирования и глобальному оптимуму. Находя производную по направление , мы определяем, является ли направление "l" невыгодным или выгодным в смысле приближения к оптимуму.

Пример.

В задаче выпуклого программирования (ВП) нужно найти минимум функции при ограничениях: х₁ + х₂ ≤ 5, х ≥ 0, х₂ ≥0.

Взяв за Х₀ точку (1; 1), проверить, приблизимся ли мы к оптимуму по направлению: а) l = (2; 1); б) l₁ = (-2; 1).

Решение.

Несколько определений ВП: дважды дифференцируемая функция F (x) = F (x₁, x₂, …, x_n) является выпуклой в том и только в том случае, когда

(3)

для любых х ∈ М и Δх_i, Δх_j, не обращающихся в нуль одновременно. Чтобы использовать это условие для определения выпуклости конкретной функции, часто применяют критерий Сильвестра (англ. математик, 1814 – 1897): условие (3) выполняется тогда и только тогда, когда неотрицательны все главные ??? Δ_k матрицы вторых частных производных, т.е. определители:

, , k = 1, …, n (4)

Если все Δ_k> 0, то неравенство (3) выполняется как строгое, и тогда функция F является строго выпуклой.

По критерию Сильвестра (4) убедимся, что функция Z является выпуклой при х₁ ≥ 0, х₂ ≥ 0.

Находим ; ; значит ; .

Отсюда, учитывая, что , по формуле (В – 6) получаем:

,

.

Таким образом, в направлении "l" функция Z убывает и по этому направлению мы приближаемся к оптимуму, а в направлении l₁ функция возрастает, т.е. мы удаляемся от оптимума.

Так как направления градиента целевой функции является направлением ее наискорейшего роста, то при отыскании максимума вогнутой функции (минимума выпуклой) в качестве l часто берется и тогда формула (2) принимает вид

, если имеется Z_max (5)

или

, если имеется Z_min (6)

Методы спуска, в которых итерационная последовательность (1) находятся по формуле (5) или (6), называются градиентными. Друг от друга они отличаются способами выбора длины шага λ и алгоритмами нахождения x_k+1. Если величина λ выбирается так, чтобы приращение функции ΔZ при перемещении из точки x_k в точку x_k+1 было наибольшим (при отыскании Z_max) или наименьшим (при отыскании Z_min), то градиентный метод называют методом скорейшего спуска, см. рис. 2.

РИСУНОК!!!!!!!

Перемещаемся из точки Х₀ в направлении мы не должны в некоторый момент "проскочить" мимо точки Х₁, в которой достигается искомый максимум.

Т.о. длина шага λ скорейшего спуска в формулах (5), (6) выбирается так, чтобы при этом λ достигался экстремум функции . При этом при нахождении точки х_k+1 предыдущая точка х_k считается уже известной, а Z (х_k) и (х_k) являются посторонними величинами, а функция ΔZ – функцией одной переменной λ.

Продифференцировав функцию ΔZ с учетом выражения х_k+1 по формулам (5 и 6) и выражения градиента в точке х_k, , получим, что необходимое условие экстремума примет вид:

(7)

Выражение (7) – более компактно, если использовать скалярное произведение векторов:

(8)

Для случая функции двух переменных метод скорейшего спуска имеет простую геометрическую интерпретацию. Для любого "k" луч, идущий от точки х_k к точке х_k+1, перпендикулярен к линии уровня функции Z, проходящей через точку х_k (так как направлен по градиенту), и касается линии уровня, проходящей через точку х_k+1 (т.к. ввиду условий [5, 6] он перпендикулярен к следующему лучу, который в свою очередь перпендикулярен к этой линии уровня). Таким образом, на плоскости скорейший спуск происходит по двум взаимно перпендикулярным направлениям, как показано на рис. 3.

РИСУНОК!!!!!!

Д. Общая постановка задачи динамического программирования, [ДП].

Динамическое программирование (ДП) – метод оптимизации, приспособленный к операциям, в которых процесс принятия решений может быть разбит на этапы (шаги). Такие операции называют многошаговыми. Начало развития ДП относится к 50-м годам ХХ в., оно связано с именем американского математика Р.Э. Беллмана.

Если модели линейного программирования можно использовать для принятия крупномасштабных планов, то модели ДП применяют для решения задач оперативного управления, например, планирование производства пищевой скоропортящейся много ассортиментной продукции в условиях колеблющегося спроса, при распределении капитальных вложений между новыми направления их использования, управления запасами, распределения фондов между предприятиями с целью получения максимальной фондоотдачи и др.

Общая постановка задачи ДП.

В результате управления (объект управления), система S переводится из начального состояния S₀ в состояние Ŝ, при этом процесс управления разбивается на "n" шагов, т.е. решение принимается последовательно на каждом шаге, а управления, переводящее систему S из начального состояния в конечное, представляет собой совокупность "n" пошаговых управлений.

Обозначим через х_k управление на "k-м" шаге (k = 1, 2, 3, …, n). Переменные х_k удовлетворяют некоторым ограничениям и называются допустимыми. х_k может быть числом, точкой в k-мерном пространстве, качественным признаком.

Пусть х (х₁, х₂, …, х_n) – управление, переводящее систему S из состояния S₀ в состояние Ŝ, S_k – состояние системы после k-го шага управления. Получаем последовательность состояний S₀, S₁, …, S_k-1, S_k, …, S_n-1, S_n = Ŝ, которую изобразим окружностями на рис.1.

Показатель эффективности рассматриваемой управляемой операции – целевая функция – зависит от начального состояния и управления:

Z = F (S₀, X) (1)

сделаем несколько предположений:

1. Состояние S_k системы в конце "k-го" шага зависит только от предшествующего состояния S_k-1 и управление на "k-м" шаге Х_k (и не зависит от остальных предшествующих состояний и управлений). Это называется отсутствием последействия. Сформулированное положение можно записать в виде уравнений:

S_k = φ_k (S_k-1, Х_k); k = 1, 2, 3, …, n (2)

которое называют уравнением состояний.

2. Целевая функция (1) является аддитивной от показателя эффективности каждого шага. Обозначим показатель эффективности k-го шага через

Z_k = f_k (S_k-1, Х_k); k = 1, 2, 3, …, n (3)

тогда

(4)

Задача пошаговой оптимизации (задача ДП) формируется так: определить такое допустимое управление Х, переводящее систему S из состояния S₀ в состояние Ŝ, при котором целевая функция (4) принимает наибольшее (наименьшее) значение.

Особенности ДП:

1. Задача оптимизации интерпретируется как "k"-шаговый процесс управления.

2. Целевая функция равна сумме целевых функций на каждом шаге.

3. Выбор управления на k-ом шаге зависит только от состояния системы к этому шагу, не влияет на предыдущие шаги (нет обратной связи).

4. Состояние S_k после k-го шага управления зависит только от предшествующего состояния S_k-1 и управления Х_k (отсутствие последействия).

5. На каждом шаге управление Х_k зависит от конечного числа управляющих переменных, а состояние S_k – от конечного числа параметров.

Существуют различные способы решения подобных задач. Рассмотрим вычислительную схему ДП, связанную с принципом оптимальности и использующей рекуррентные соотношения.

Принцип оптимальности и управления Р. Беллмана.

Принцип оптимальности был сформулирован Р. Беллманом в 1953 году. Формулировка принципа Беллманн-Вентуель:

Каково бы ни было состояние S системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.

Р. Беллман показал, что основное требование – это то, что процесс должен быть без обратной связи, т.е. управление на данном шаге не оказывает влияние на предшествующие шаги. Поэтому решение на каждом шаге оказывается наилучшим сточки зрения управления в целом.

Управление Беллмана.

Введем ряд новых обозначений, которые нужно четко усвоить. На каждом шаге любого состояния системы S_k-1 решение Х_k нужно выбирать с "оглядкой", т.к. этот выбор влияет на последующее состояния S_k и дальнейший процесс управления, зависящий от S_k. Это следует из принципа оптимальности. Но всегда есть один шаг, последний, который можно для любого состояния S_k-1 планировать локально-оптимально, исходя только из соображений этого шага.

Рассмотрим "n-й" шаг:

S_n-1 – состояние системы к началу "n" – шага;

S_n = Ŝ – конечное состояни;

Х_n – управление на "n" – шаге;

F_n (S_n-1, X_n) – целевая функция "n"-го шага.

Согласно принципу оптимальности, X_n нужно выбрать так, чтобы для любых состояний S_n-1 получить максимум целевой функции на этом шаге.

Обозначим через максимум целевой функции – показателя эффективности "n"-го шага при условии, что к началу последнего шага система S была в произвольном состоянии S_k-1, а на последнем шаге управление было оптимальным.

называется условным максимум целевой функции на "n"-шаге. Очевидно, что:

(5)

Максимизация ведется по всем допустимым управлениям х_k. Решение х_n, при котором достигается , также зависит от S_n-1 и называется условным оптимальным управлением на "n"-м шаге. Оно обозначается через .

Решив одномерную задачу локальной оптимизации по управлению (5), найдем для всех возможных состояний S_n-1 две функции: и .

Рассмотрим теперь двухшаговую задачу: присоединим к "n"-му шагу (n-1), рис. 2.

Для любых состояний S_n-2, произвольных управлений Х_n-1 и оптимальном управлении на "n" м шаге значение целевой функции на двух последних шагах равно:

(6)

Решение нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем (n-м) шаге приводило бы к максимуму целевой функции на двух последних шагах. Следовательно, нужно найти максимум выражения (6), по всем допустимым управлениям Х_n-1. Максимум этой суммы зависит от S_n-2, обозначается через и называется условным максимумом целевой функции при оптимальном управлении на двух последних шагах.

Соответствующее управление Х_n-1 на (n-1)-м шаге обозначается через и называется условным оптимальным управлением на (n-1)-м шаге.

(7)

выражение, стоящее в фигурных скобках (7), зависит только от S_n-2 и Х_n-1, т.к. S_n-1 можно найти из уравнения (2) при k = n-1.

и подставить вместо S_n-1 в функцию .

В результате максимизации только на одной переменной Х_n-1, согласно уравнению (7) вновь получается две функции:

и .

Если рассмотреть трехшаговую задачу, то к двум последним шагам присоединяется (n-2) и т.д.

Обозначим через условный максимум целевой функции, полученной при оптимальном управлении на (n-k+1) шагах, начиная с k-го до конца, при условии, что к началу k-го шага система находилась в состоянии S_k-1. Фактически эта функция равна:

Тогда

Рис. 3

Целевая функция на (n-k) шагах (рис.3) при произвольном управлении Х_k на k-м шаге и оптимальном управлении на последующих (n-k) шагах равна

Согласно принципу оптимальности, Х_k выбирают из условия максимума этой суммы:

Управление Х_k на k-м шаге, при котором достигается максимум в (8), обозначается через и называется условным оптимальным управлением на k-м шаге. В правую часть уравнения (8) следует вместо S_k подставить выражение S_k = φ_k (S_k-1, X_k), найденное из уравнений состояния.

Уравнение (8) называют уравнением Беллмана. Это рекуррентные соотношения, позволяющие найти предыдущее значение функции, зная последующие. Если из (5) найти значение , то при k = n-1 из (8) можно определить, решив задачу максимизации для всех возможных значений S_n-2, выражения для и соответствующее . Далее, зная , находим, используя (5) и (8) называется условной оптимизацией, в результате которой получается две последовательности:

, , …, , - условные максимумы целевой функции на последнем, на двух последних, на …n шагах и

, , …, , - условные оптимальные управления на n-м, (n-1)-м, … "λ"-м шагах. Используя эти последовательности, можно найти решение задачи ДП при данных "n" и "S₀".

- условный максимум целевой функции за "n" шагов при условии, что к началу 1-го шага система была в состоянии S₀, т.е.

(9)

Далее необходимо использовать последовательность условных оптимальных управлений и уравнений состояний (2).

При фиксированном S₀ получаем . Далее из уравнений (2) находим и подставляем это выражение в последовательность условных оптимальных управлений:

и т.д. по цепочке:

→ → → =>

→ … → =>

т.о. получаем оптимальные решение задачи ДП:

.

Стрелка → означают использование уравнений состояния,

стрелка => означает последовательность условных оптимальных управлений.

Г. Пример: Задача об оптимальном распределении ресурсов между предприятиями объединения па "n" лет.

Если все требования, предъявленные к задаче, решаемой методом ДП, выполнимы, то построение модели ДП и применение метода ДП для решения задачи сводится к следующим этапам:

Общая схема применения метода ДП	1.	Выбирают способ деления процесса управления на шаги.
	2.	Определяют параметры состояния - Sk и переменные управления на каждом шаге - Хk.
	3.	Записывают уравнения состояний.
	4.	Вводят целевые функции "k"-го шага и суммируют целевую функцию.
	5.	Рассматривают условные максимумы (минимумы) и условное оптимальное управление на “k”-м шаге: , k = n, n-1, …, 2, 1.
	6.	Записываем основные для вычислительной схемы ДП уравнения Р. Беллмана для и , k = n-1, n-2, …, 2, 1.
	7.	Решают последовательно уравнения Беллмана (условная оптимизация) и получают две последовательности функций: и .
	8.	После выполнения условной оптимизации получают оптимальное решение для конкретного начального состояния S0: а) и б) по цепочке оптимальное управление: .

Решая задачи, следует по возможности этой схемы. Рассмотрим, как работает эта схема на примере задачи об оптимальном распределении ресурсов между двумя предприятиями объединенная на "n" лет.

Пример.

Планируется деятельность двух предприятий одного производственного объединения на "n" лет.

Начальные ресурсы S₀. Средства Х, вложенные в первое предприятие в начале года, дают в конце года прибыль f₁ (x) и возвращаются в размере q₁ (x) < x; аналогично для второго предприятия функция прибыли f₂ (x), а возврата q₂ (x) < x. В конце года все возвращенные средства заново переопределяются между первым и вторым предприятиями. Новые средства не поступают.

Требуется распределить имеющиеся средства S₀ между двумя предприятиями на "n" лет так, чтобы суммарная прибыль от обеих отраслей за "n" лет оказалась максимальной.

Необходимо:

а) построить модель ДП для задачи и вычислительную схему;

б) решить задачу при условии, что S₀ = 10000 ед.;

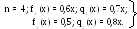
Решение.

а) Процесс распределения средств между двумя предприятиями производственного объединения производится во времени. Решения принимаются в начале каждого года, осуществляется деление на шаги: номер шага – номер года. Управляемая система – два предприятия объединения "Молоко", и управление состоит в выделении средств каждому предприятию в очередном году. Параметры состояния к началу "k"-го года – S_k-1, (k = 1, 2,…,n) – количество средств, выделенных первому предприятию, и y_k – второму предприятию. Так как все средства S_k-1 распределяются, то y_k = S_k-1 – X_k, и поэтому управление на "k"-шаге зависит от одной переменной "X_k",

т.е. X_k (x_k, S_k-1-x_k)

Уравнение состояний

S_k = q₁ (x_k) + q₂ (S_k-1-x_k) (1)

Суммарный показатель эффективности "k"-го шага – прибыль, полученная в конце "k"-го года от обеих отраслей:

F₁ (x_k) + f₂ (S_k-1-x_k) (2)

Суммарный показатель эффективности – целевая функция задачи – прибыль за "k" лет:

(3)

Пусть - условная оптимальная прибыль за [n-(k+1)] лет, начиная с "k"-го года до "n"-го года включительно, при условии, что имеющиеся на начало "k"-го года средства S_k-1 в дальнейшем распределились оптимально. Тогда оптимальная прибыль за "n" лет

.

Уравнения Беллмана имеют вид:

(4)

(5)

k = n-1, n-2, …, 2, 1.

б) Используем конкретные данные.

Уравнение состояний (1) примет вид:

S_k = 0,7x_k+0,8 (S_k-1 – x_k), или S_k = 0,8S_k-1 – 0,1x_k (6)

Целевая функция k-го шага (2):

0,6x_k + 0,5 (S_k-1 - x_k) = 0,1x_k + 0,5S_k-1

Целевая функция задачи:

(7)

Функциональные уравнения:

(8)

и

(9)

Проведем условную оптимизацию.

IV шаг. Используем уравнение (8). Обозначим через Z₄ функцию, стоящую в скобках, Z₄=0,1x₄+0,5S₃. Функция Z₄ – линейная, возрастающая, так как угловой коэффициент 0,1 больше нуля. Поэтому максимум достигается на конце интервала {0,S₃}, рис. 1. Следовательно, при .

III шаг. Уравнение: .

,

Найдем S₃ из уравнений состояний (6): S₃ = 0,8S₂ - 0,1x₃ и подставим в выражение .

Как и в предыдущем случае, максимум достигается при x₃ = S₂, т.е. при .

II шаг. Из уравнения состояния: S₂= 08S₁ - 0,1x₂. Поэтому уравнение (8) при k = 2 примет вид: .

Линейная относительно х₂ функция убывает на отрезке [0;S₁], и поэтому ее максимум достигается при х₂=0, рис.2:

при

I шаг. S₁=0,8S₀-0,1x₁. Уравнение (δ) при к=1 имеет вид:

Как и в предыдущем случае, максимум достигается в начале отрезка, т.е.

при .

На этом условная определяющая заканчивается. Используя ее результат и исходные данные получаем , Z_max=15528, действительно:

; y^*=S₀=10000 (все средства выделены II-му предприятию)→

(все средства выделяются II-му предприятию)→

→, →

(все средства выделяются I-му предприятию)→

→,

(все средства выделяются I-му предприятию).

Оптимальная прибыль за 4 года, полученная от двух предприятий производственного объединения «Молоко» при условии, что I-е предприятие получается по годам (0; 0; 6400; 4880), а II-е предприятие – соответственно (10000; 8000; 0; 0).