Предел функции. Теорема Гейне

Рассмотрим функцию , определенную на множестве . Пусть . Точка называется предельной или точкой сгущения множества , если в любой окрестности этой точки найдутся точки множества, отличные от . В этом случае из множества можно выделить последовательность , сходящуюся к . К числу предельных точек можно отнести внутренние точки множества, входящие в состав вместе с некоторой окрестностью. Очевидно, что в общем случае точка сгущения может оказаться не внутренней. В качестве примера можно привести множество рациональных чисел , все точки которого в любой окрестности содержат кроме рациональных чисел и иррациональные, которые в не входят.

Множество называется замкнутым, если оно содержит все свои предельные точки, и множество называется открытым, если оно состоит из одних внутренних точек.

Функция , определенная на множестве имеет предел в точке сгущения : если для любого найдется такое , что при .

Указанное определение опирается на понятие функции и именуется определением предела по Коши.

Существует эквивалентное определение предела, вытекающее из теоремы Гейне.

Эта теорема сводит понятие предела функции к пределу сходящихся последовательностей значений функции , задаваемых для различных последовательностей , стремящихся к . Можно легко показать, что при любом выборе последовательности , если существует предел соответствующих последовательностей , то этот предел единственен.

Функцию, имеющую предел не следует путать с ограниченной функцией. Функция , имеющая предел при , ограничена в некоторой окрестности точки . Обратное утверждение не верно: ограниченная функция может не иметь предела.

Пределы обладают следующими свойствами:

• Если – есть постоянная функция, то ;

• Если существуют , и в некоторой окрестности точки функция 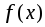ограничена, т.е. , тогда ;

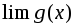• Если существуют и при каком-то условии, то (при том же условии). Это свойство справедливо для любого конечного числа функций;

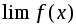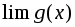• Если существуют и при каком-то условии, то (при том же условии). Это свойство также справедливо для любого конечного числа функций, в частности, справедлива формула ;

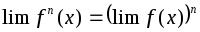• Если существуют и при каком-то условии, то (при том же условии);

• Если и существуют , и , то .

Односторонние пределы

В определении предела функции предполагалось, что произвольным образом. Если при вычислении предела функции при считать, что , то получают односторонний предел справа или правосторонний предел функции в точке . Если же считать, что и , то получают односторонний предел слева или левосторонний предел.

Так, например, односторонние пределы функции , изображенной на Рис. 2, соответственно, равны: и .

Правосторонний предел обозначают символом , левосторонний ‑ символом . Таким образом:

.

В этих определениях предполагается, что функция определена на некотором промежутке соответственно справа или слева от точки сгущения .

Для того, чтобы у функции в точке существовал двусторонний предел , необходимо и достаточно, чтобы существовали левосторонний и правосторонний пределы и функции в точке , и эти пределы были равны между собой: .

Пример.

Пример.