Бесконечный предел

Наряду с бесконечно малыми существуют и бесконечно большие величины, являющиеся обратными по отношению к бесконечно малым. Поэтому является бесконечно большой (, при ), если такое, что при .

Говорят, что предел последовательности равен , если для такое, что выполняется неравенство: .

В отличие от бесконечно малых последовательностей, бесконечно большие могут не иметь предела. Например, по модулю неограниченно растет, но сама величина не имеет определенного стремления.

Замечательные пределы

Важную роль на практике играют замечательные пределы, используемые, например, при вычислении пределов функций. Приведем два замечательных предела:

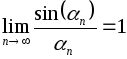1. , где

2. 

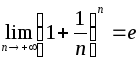
Покажем, что

Для простоты примем, что (см. Рис.1.), причем, так как дуга стремится к нулю при , то можно считать, что (указанное допущение не является принципиальным, но позволит использовать геометрическую интерпретацию). Сравним величины и с помощью диаграммы, построенной в первом квадранте.

Площади треугольников , и сектора соотносятся следующим образом:

Отсюда , и после деления на , получим , а для обратных величин . Так как при последовательность , а, следовательно, , то видно, что последовательность заключена между двумя последовательностями, имеющими общий предел, равный 1. Таким образом, можно сделать вывод, что для бесконечно малой последовательности , справедливо равенство .

При анализе второго замечательного предела необходимо показать, что последовательность является монотонно возрастающей и ограниченной сверху. Для этого можно воспользоваться формулой бинома Ньютона, положив, что , а . Тогда:

,

.

Таким образом, , так как в каждом слагаемом множители вида имеют меньшую величину по сравнению с при одном и том же , а также выражение для имеет на одно положительное слагаемое больше.

Ограниченность сверху можно показать следующим образом:

.

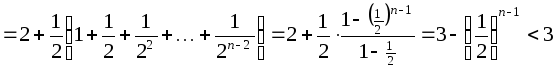Таким образом, в соответствии с теоремой о монотонной последовательности имеет предел:

,

который обозначается (основание натурального логарифма ).

В высшей математике употребляются почти исключительно натуральные логарифмы, поскольку многие формулы для них оказываются более простыми, чем для логарифмов других систем.

Принцип сходимости

Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга.

Лемма Кантора. Пусть дана последовательность промежутков , где . Если при этом , то последовательности и имеют равные пределы: .

Теорема Больцано – Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Сходимость последовательности к конечному пределу означает, что все элементы последовательности с достаточно большими номерами мало отличаются от числа и, следовательно, мало отличаются друг от друга.

Принцип сходимости формулируют в виде теоремы, называемой критерием Коши.

Критерий Коши. Последовательность сходится тогда и только тогда, когда такое, что выполняется неравенство: .