13. Метод Марквардта

Этот метод является комбинацией методов градиентного спуска и Ньютона, в котором удачно сочетаются положительные свойства обоих методов. Движение в направлении антиградиента из точки , расположенной на значительном расстоянии от точки минимума , обычно приводит к существенному уменьшению целевой функции. С другой стороны, направление эффективного поиска в окрестности точки минимума определяются по методу Ньютона.

Отметим, что в различных модификациях метода Ньютона требуется большое количество вычислений, так как на каждой итерации следует сначала вычислить элементы матрицы , а затем решать систему линейных уравнений. Применение конечно разностной аппроксимации первых и вторых производных только ухудшит ситуацию.

Поэтому в последнее время построено много, так называемых квазиньютоновских методов, как с аналитическим вычислением градиента и матрицы Гессе, так и с их конечно разностной аппроксимацией. Эти методы опираются на возможность аппроксимации кривизны нелинейной целевой функции без явного формирования ее матрицы Гессе. Данные о кривизне накапливаются на основе наблюдения за изменением градиента во время спуска.

Различные формы таких методов, часто называемые методами секущих, показали неплохие результаты в научных и технических исследованиях.

В соответствии с методом Марквардта, направление поиска определяется равенством

(1), а новая точка задается формулой .

В системе (1) I – единичная матрица, – матрица Гессе, .

В последней формуле коэффициент перед взят равным 1, так как параметр в (1) позволяет менять и длину шага, и его направление.

На начальной стадии поиска параметру приписывается некоторое большое значение, например 10⁴, так что

Таким образом, большим значением соответствует направление поиска

то есть направление наискорейшего спуска.

Из формулы (1) можно заключить, что при уменьшении λ до нуля вектор изменяется от направления, противоположного градиенту, до направления, определяемому по Ньютону. Если после первого шага получена точка с меньшим значением целевой функции, то есть , следует выбрать и реализовать еще один шаг. В противном случае нужно положить , где , и вновь реализовать предыдущий шаг.

Заметим, что недостатком метода Ньютона является то, что если матрица Гессе не является положительно определенной, то Ньютоновский шаг не приводит к убыванию функции. Поэтому “исправление” Гессиана в соответствии с формулой модифицирует матрицу и при соответствующем выборе делает ее положительно определенной, так как единичная матрица положительно определена.

Приведем теперь алгоритм метода:

Задать 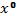– начальное приближение к , M-максимально допустимое количество итераций и – параметр сходимости.
Положить .
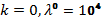Вычислить .
Проверить ||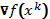||. Можно взять ||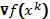|| = . Если да, то перейти к п.11.
Проверить 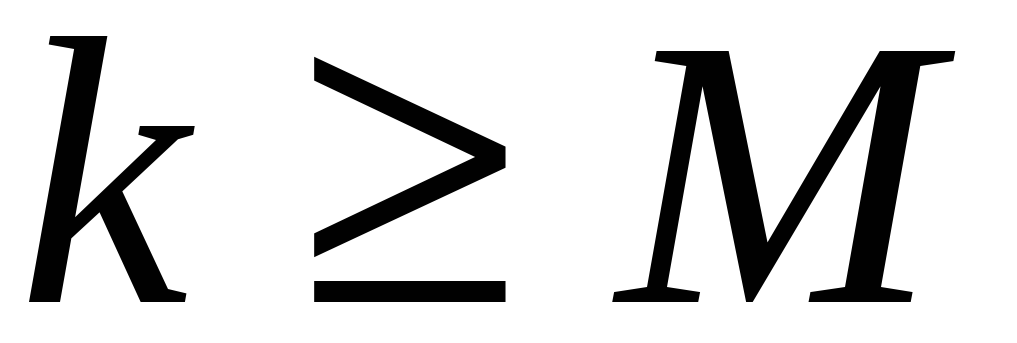? Если да, то перейти к п.11.
Вычислить шаг 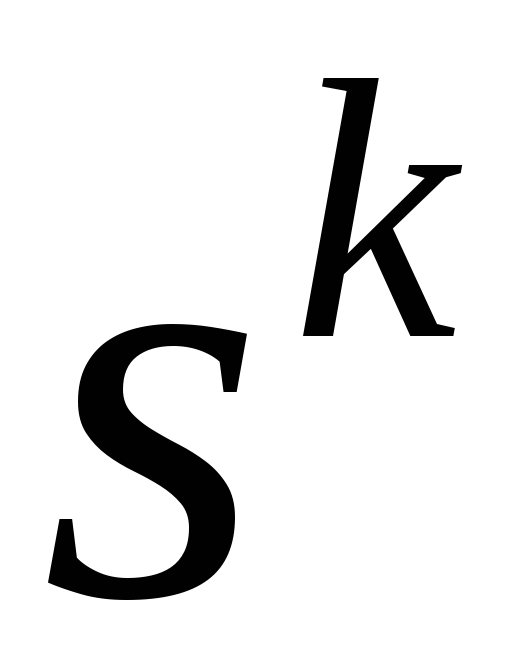, решив систему .
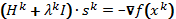Положить .
Проверить: 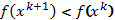. Если да, то перейти к п.9, иначе к п.10.
Положить ,. Перейти к п.3.
Положить 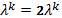. Перейти к п.6.
Вывод результатов: 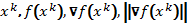, k