3.4.3. Площадь области поверхности

Пусть F – поверхность с краем, удовлетворяющим следующим условиям:

1) F гомеоморфна замкнутому кругу;

2) F является частью некоторой гладкой поверхности Ф;

3) край поверхности F – кусочно-гладкая линия (т.е. гладкая во всех точках, за исключением конечного числа точек).

Для такой поверхности можно вычислить площадь. Поверхность, имеющая площадь, называется квадрируемой.

Теорема. Если поверхность F задана параметрическими уравнениями x = x(u, v), y = y(u, v), z = z(u, v), то площадь этой поверхности вычисляется по формуле:

S(F) = du dv,

где D – соответствующая поверхности F область изменения переменных u и v.

Следует из того, что S(F) =

Имеем: || = || · || sin (a, b) = || · || = , тогда

| | = =

Пример. Найти площадь четырехугольника u = 0, u = a, v = 0, v = 1, расположенного на поверхности x = u cos v, y = u sin v, z = av.

Е = 1, F = 0, G = a² + u²

EG – F² = a² + u²

S = = = =

= = = ().

Замечание. Таким образом, зная первую квадратичную форму поверхности, можно решать следующие метрические задачи:

1) вычислить длины дуги гладкой линии, лежащей на поверхности;

2) вычислить угол между двумя гладкими линиями, лежащими на поверхности и имеющими общую точку;

3) вычислить площадь гладкой компактной поверхности.

Учитывая эти приложения первой квадратичной формы, её часто называют метрической формой данной поверхности.

3.5. Вторая квадратичная форма поверхности

Пусть Ф – С²-гладкая поверхность и – некоторая её параметризация,  =  – единичный вектор нормали к поверхности, – второй дифференциал функции .

Определение. Второй квадратичной формой поверхности Ф называется скалярное произведение: II = ·.

= d( du + dv) = du² + 2 du dv + dv²

II = du² + 2 du dv + dv²

= L, = M, = N

II = L du² + 2M du dv + N dv²

Так как | | = , то:

L = , M = , N =

Пример. Найти вторую квадратичную форму поверхности Ф: x = u cos v, y = u sin v, z = u

(cos v; sin v; 1) (0; 0; 0), (–sin v; cos v; 0)

(–u sin v; u cos v; 0) (–u cos v; –u sin v; 0)

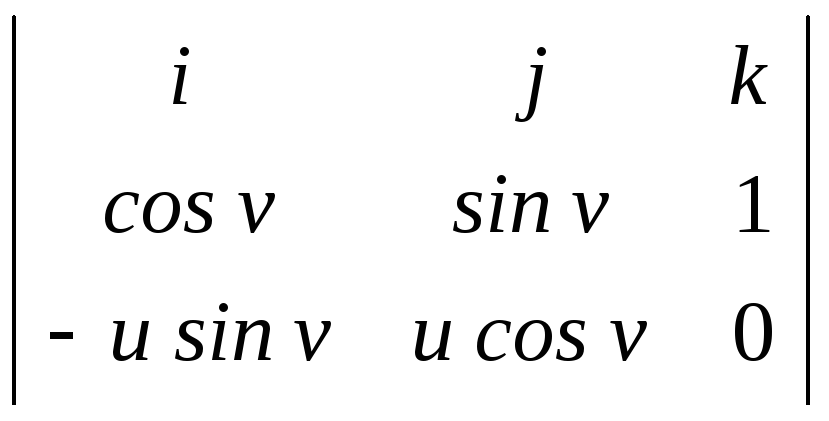= = (–u cos v; –u sin v; u) => = (–; –; )

| | =

L = = 0

M = = – + 0 = 0

N = = => II = dv²

3.5.1. Нормальная кривизна кривой на поверхности

Ф – С²-гладкая поверхность, – некоторая её параметризация

 – С²-гладкая кривая на Ф, внутренние уравнения которой u = u(s), v = v(s).

Кривая  задается вектор-функцией = (u(s), v(s)) класса С². Пусть X(u, v) – произвольная точка на .

По первой формуле Френе: = k , где k – кривизна  в точке X.

Имеем: = k · = k cos , где  – угол между векторами и .

С другой стороны:

= + 2 + + +

Отсюда: · =

Вдоль  ds² = I => k cos  = =

Замечание. Правая часть последнего равенства зависит только от направления кривой  в точке X, так как в ней E, F, G, L, M, N – некоторые фиксированные числа. Для всех кривых поверхности Ф, проходящих через точку X и имеющих в ней одно и то же направление (касательную), отношение постоянно. Его обозначают k_n.

Определение. k_n = k cos  = называют нормальной кривизной кривой на поверхности.

Определение (наглядный смысл нормальной кривизны). Нормальным сечением поверхности называется кривая, являющаяся пересечением поверхности с плоскостью, проходящей через нормаль.

Нормальная кривизна поверхности с точностью до знака совпадает с кривизной нормального сечения в данном направлении.