6. Уравнение Бернулли

Уравнением Бернулли называется уравнение вида

Решение.

1. Можно интегрировать это уравнение как линейное, полагая, как и ранее, . Отсюда .

Решая его, получим:

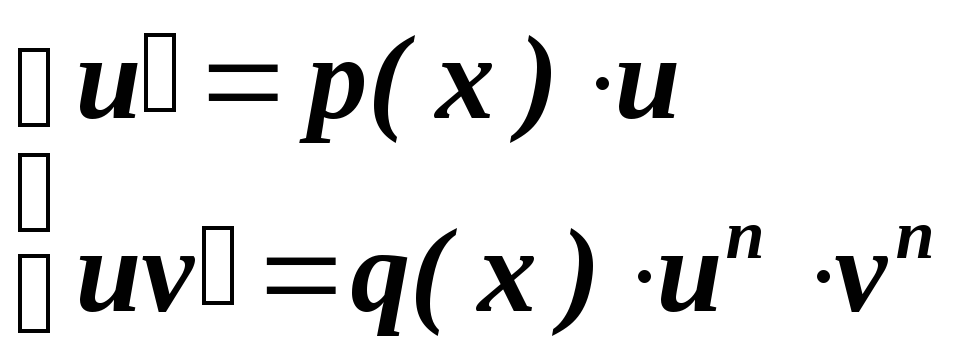
2. Это уравнение сводится к линейному, если разделить его на :

Делаем замену

.

Продифференцировав замену, найдем что

.

Или

.

Подставляя в исходное уравнение, получим

которое является линейным дифференциальным уравнением первого порядка.

Пример. Проинтегрировать уравнение .

Введем переменную . Найдя производную и подставив ее в исходное уравнение, получим:

или

.

Это уравнение распадается на два .

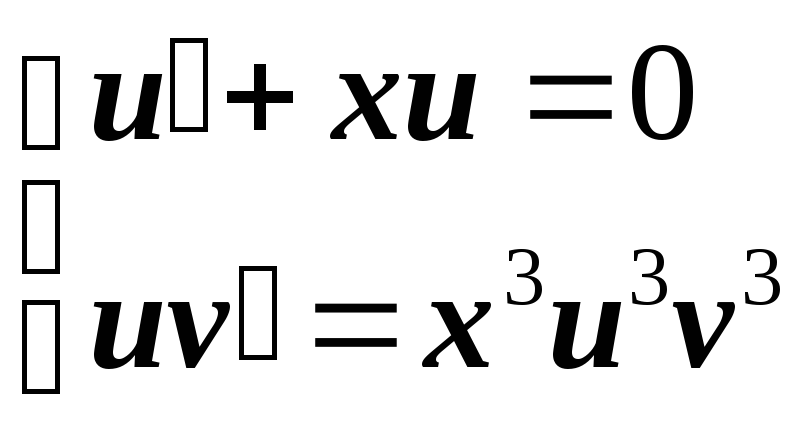Решаем первое

Решаем второе

Интегрируем правую часть:

Отсюда

.

В результате получим

.

В итоге

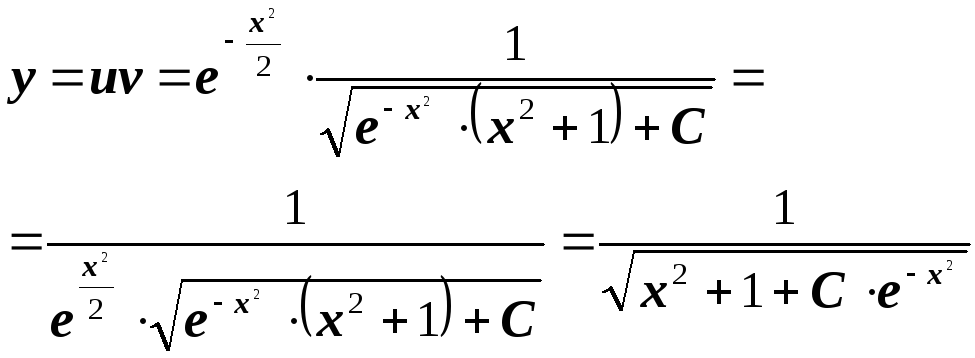
7. Уравнения в полных дифференциалах

Уравнением в полных дифференциалах называется уравнение

левая часть, которого является полным дифференциалом некоторой функции, т.е.

Общий интеграл уравнения определяется формулой

.

Далее, поскольку

то из условия следуют уравнения

которыми определяется функция . Необходимое и достаточное условие того, что уравнение является уравнением в полных дифференциалах, выражается равенством

которое вытекает из условия равенства смешанных производных:

.

Если левая часть исходного уравнения не является полным дифференциалом, но становится таковым при умножении на некоторую функцию - , то называется интегрирующим множителем.

Интегрирующий множитель зависит только от , т.е. , если

и зависит только от , если

Пример. Проинтегрировать уравнение .

Имеем , .

Мы видим, что и, следовательно, это уравнение – дифференциальное уравнение в полных дифференциалах.

Поэтому .

Аналогично

.

Сравнивая с найденным, запишем:

.

Отсюда вытекает, что

Отсюда

.

Следовательно, интеграл уравнения имеет вид:

.

8. Дифференциальные уравнения второго порядка.

Дифференциальным уравнением второго порядка называется уравнение относительно искомой функции, ее первой и второй производной. В общем виде это уравнение записывается как

где заданная функция указанных аргументов.

Общим решением дифференциального уравнения второго порядка называется функция от и двух независимых произвольных постоянных и , обращающих данное уравнение в тождество. Общее решение, заданное в неявном виде , называют общим интегралом.

Частным решением уравнения называется решение , полученное из общего путем фиксирования значений произвольных постоянных: .

Задача Коши. Найти решение дифференциального уравнения второго порядка, удовлетворяющее условиям: . Числа , определяющие искомое частное решение, находятся из системы уравнений:

.

9. Уравнения 2-го порядка, допускающие понижение порядка.

Если уравнение разрешимо относительно старшей производной, то его можно представить в виде

.

К простейшим интегрируемым дифференциальным уравнениям второго порядка относятся уравнения, для которых функция, стоящая в правой части зависит только от одного из трех аргументов

(А)

(Б)

(В)

Общее решение уравнения (А) находится двукратным интегрированием.

Уравнения (Б) (В) интегрируются подстановкой

которая дает возможность свести их к уравнениям с разделяющимися переменными

Уравнение , подстановкой приводится к уравнению первого порядка , в котором роль независимой переменной играет .

Пример.

Проинтегрировать дифференциальное уравнение:

.

Делаем замену . Отсюда

.

В результате исходное уравнение примет вид

.

Преобразуем его следующим образом:

.

Это уравнение распадается на два.

1.

2. .

Используя, что , найдем:

3. .

Или . Отсюда

4. . Возвращаемся к старой переменной.

5. . Интегрируем.

6.