4. Интегрирование подстановкой.

Теорема: Имеет место равенство

где функция непрерывно дифференцируема на , , и непрерывна на - образе отрезка при помощи функции .

Доказательство. Пусть и - первообразные функции соответственно и . Тогда справедливо тождество

где - некоторая постоянная. Поэтому

На основании формулы Ньютона-Лейбница, левая часть этого равенства равна левой части равенства теоремы, соответственно и правые части, что доказывает теорему.

Пример 1. Найти интеграл .

Сделаем замену переменных: . Найдем дифференциал : . В результате наш интеграл примет вид:

Преобразуем подынтегральное выражение:

Взяв этот интеграл, получим:

.

5. Интегрирование по частям в определенном интеграле.

Теорема. Справедлива формула интегрирования по частям для определенного интеграла

где и - непрерывно дифференцируемые на функции.

Доказательство. Произведение имеет на непрерывную производную

Поэтому по теореме Ньютона-Лейбница

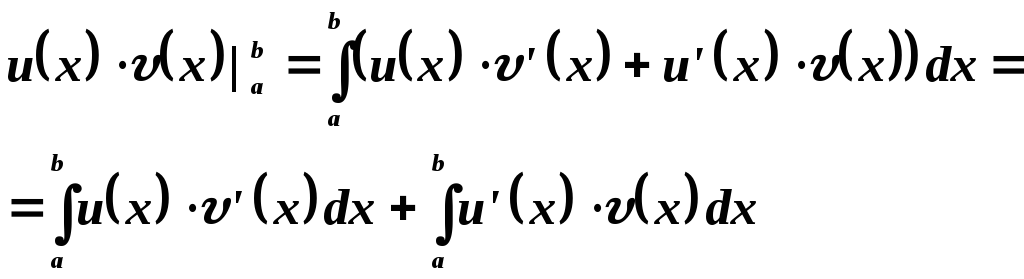
Этим теорема доказана.

Например, найти интеграл .

Обозначим и . Тогда . Поэтому

Или, окончательно

.

Если - четная функция , то

Пример 2. Найти интеграл .

Преобразуем этот интеграл к виду

Сделаем замену . В результате пределы интегрирования изменятся: и . В результате получим:

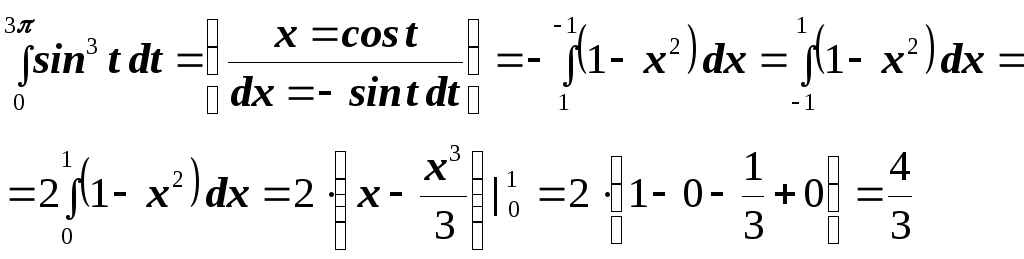
Далее, если - нечетная функция , то

.

Если - периодическая функция периода - , то

.

Такие особенности в некоторых случаях упрощают процесс интегрирования.

Пример 3. Вычислить интеграл .

Преобразуем этот интеграл к виду:

Пределы интегрирования во втором интеграле представим как:

Согласно свойству периодической функции, перепишем это выражение:

Преобразуем далее

Пример 4. Определить объем продукции, произведенной рабочим за третий час рабочего дня, если производительность труда характеризуется функцией .

График этой функции имеет вид, изображенный на рисунке.

Решение. Если непрерывная функция характеризует производительность труда рабочего в зависимости от времени , то объем продукции, произведенной рабочим за промежуток времени от до будет выражаться формулой:

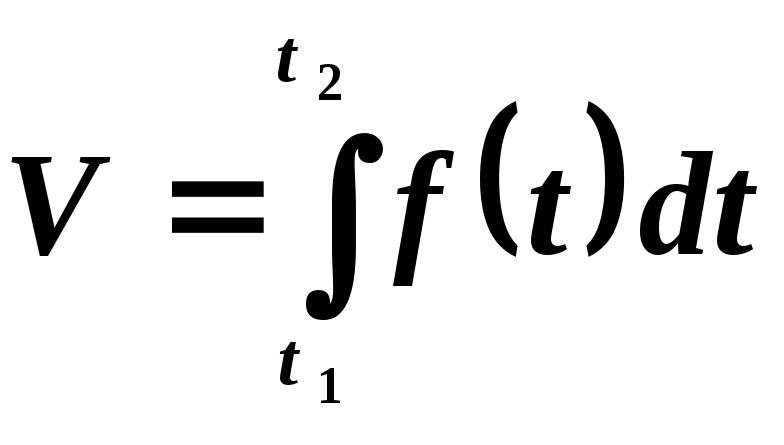
В нашем случае:

Пример 5. Определить запас товаров в магазине, образуемый за три дня, если поступление товаров характеризуется функцией .

Решение. Имеем:

6. Несобственные интегралы.

Пусть на конечном полуинтервале задана функция такая, что она интегрируема (т.е. конечна) на любом интервале , где , но неограниченна в окрестности точки . Тогда ее интеграл на , или, что то же самое, на не может существовать, так как интегрируемая функция должна быть ограничена.

Однако может случиться так, что существует конечный предел

То есть функция не ограничена, а ее интеграл ограничен. В этом случае записанный предел называют несобственным интегралом от на отрезке и записывают в виде

В таком случае говорят, что интеграл сходится. В противном случае говорят, что он расходится или не существует как несобственный риманов интеграл.

Аналогично и на полуинтервале

В связи с этим выражение

называется интегралом от с единственной особенностью в точке , если выполняется следующее условие: если конечная точка, то функция интегрируема на при любом удовлетворяющим неравенствам , и, кроме того, не ограничена в точке . Если же , то про функцию предполагается лишь, что она интегрируема на при любом конечном .

Также различают несобственные интегралы первого типа (с одним или двумя бесконечными пределами) и несобственные интегралы второго типа (от разрывных функций).

Несобственный интеграл первого рода, вычисляется обычно как

Например, найти .

Имеем .

При это выражение имеет предел . Значит .

Или, найти .

Имеем . Этот интеграл расходится.

П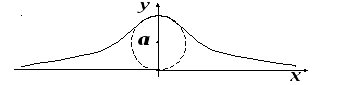 ример 6. Найти площадь бесконечной полосы (верзьера Аньези).

.

Далее, имеем .

Отсюда .

Аналогично вычисляется и первое слагаемое. В итоге получим:

.

Пример 7. Найти .

Данный интеграл - несобственный, так как подынтегральная функция терпит разрыв в точке . Однако этот интеграл сходится, так как