
- •Основные понятия
- •Дифференциальные уравнения
- •Обыкновенные дифференциальные уравнения Уравнения с
- •Графичес- Аналити- Прибли- Численное Численное
- •Метод Решение Методы
- •3.2. Методы решения. Общие положения
- •3.3. Задача Коши. Общие замечания
- •3.4. Метод Пикара
- •Так как должны выполняться условия (3.21), (3.22) можно записать в виде
- •3.6. Метод Эйлера
- •Аналогично определяем отрезки , , …
- •Так как искомую точку находим как точку пересечения прямой с ординатой , то можно записать:
- •Метод согласуется с рядом Тейлора вплоть до членов степени .
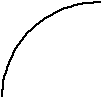
- •На рис. 11 видно, что расхождение этого метода значительно меньше расхождения обычного метода Эйлера, равного .
- •3.7. Метод РунгеКутта
- •3.8. Метод Адамса
- •(К выводу формулы метода Адамса)
Так как искомую точку находим как точку пересечения прямой с ординатой , то можно записать:
![]() .
.
Тогда окончательно формула исправленного метода Эйлера запишется так:
![]() (3.49)
(3.49)
Метод согласуется с рядом Тейлора вплоть до членов степени .
На рис. 10 видно, что
если расхождение обычного метода Эйлера
равно
![]() ,
то у исправленного метода оно составляет
,
то у исправленного метода оно составляет
![]() ,
которое существенно меньше
,
которое существенно меньше
![]() .
.
в)
модифицированный метод Эйлера.
В исправленном методе Эйлера повышение
точности результата вычисления
достигается за счет использования
вспомогательной прямой, которая
проводится с угловым коэффициентом,
равным среднему угловых коэффициентов
касательных, проведенных к искомой
кривой в соседних узловых точках
![]() и
и
![]() .
Но можно пойти и по другому пути, а
именно, в качестве вспомогательной
использовать среднюю
точку между узлами.
На этой основе строится модифицированный
метод Эйлера.
.
Но можно пойти и по другому пути, а
именно, в качестве вспомогательной
использовать среднюю
точку между узлами.
На этой основе строится модифицированный
метод Эйлера.
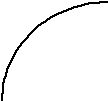
Рассмотрение этого метода начнем с его геометрической интерпретации (рис. 11).
1. Определяем среднюю
точку между соседними узлами (рис. 11
между
![]() и
и
![]() )
с абсциссой
)
с абсциссой
![]() .
.
2. Проводим, как и
в обычном методе Эйлера, касательную
![]() через точку
через точку
![]() .
.
3. Находим точку A,
находящуюся на пересечении прямой
![]() и ординаты
и ординаты
![]() .
.
4. Проводим через
точку A
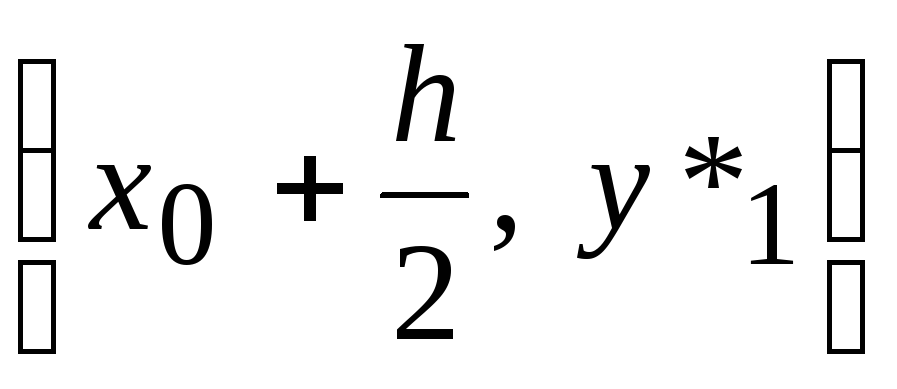 прямую
прямую
![]() ,
которая является касательной к кривой
,
которая является касательной к кривой
![]() .
.
5. Из точки
![]() проводится прямая
проводится прямая
![]() ,
параллельная
,
параллельная
![]() ,
и находится точка
,
и находится точка
![]() как точка пересечения прямой
как точка пересечения прямой
![]() с ординатой
с ординатой
![]() .
.
Ордината
![]() и будет искомым решением в точке
и будет искомым решением в точке
![]() .
.

![]()
![]()
![]()
![]()
![]()


![]()
![]()






A
![]()



![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()






![]()





![]()




h


![]()
![]()
![]()
![]()
![]()
Рис. 10 Рис. 11
Формула модифицированного метода Эйлера:
![]() ,
(3.51)
,
(3.51)
На рис. 11 видно, что расхождение этого метода значительно меньше расхождения обычного метода Эйлера, равного .
Можно показать,
что модифицированный метод Эйлера
согласуется с рядом Тейлора вплоть до
членов с
![]() .
.
Кроме всего вышесказанного, здесь можно отметить еще одну особенность методов Эйлера, а именно: даже для малых значениях шага при неблагоприятных условиях применение этих методов может дать совершенно ошибочные результаты.
3.7. Метод РунгеКутта
Наиболее употребительной является схема РунгеКутта четвертого порядка. Запишем алгоритм этого метода в виде
![]() ,
(3.56)
,
(3.56)
где
![]() (3.57)
(3.57)
![]()
![]()
![]() ,
(3.58)
,
(3.58)
![]()
Таким образом, метод
РунгеКутта
требует на каждом шаге четырехкратного
вычисления правой части уравнения
![]() .
.
В предыдущем параграфе мы рассмотрели методы Эйлера. Метод Эйлера и его модифицированные варианты могут рассматриваться как методы РунгеКутта первого и второго порядков. Метод РунгеКутта требует большего объема вычислений, однако это окупается повышенной точностью, что дает возможность проводить счет с большим шагом. Другими словами, для получения результатов с одинаковой точностью в методе Эйлера потребуется значительно меньший шаг, чем в методе РунгеКутта.
Для контроля правильности выбора шага используется следующее правило:
При каждом
![]() вычисляется дробь
вычисляется дробь
![]() .
(3.59)
.
(3.59)
Если A больше нескольких сотых, т.е. больше нескольких процентов, следует уменьшить шаг h (обычно следующий шаг берут h / 2).
Погрешность метода
РунгеКутта
пропорциональна
![]() ,
где n
порядок метода (так как здесь мы
рассматриваем метод РунгеКутта
четвертого порядка, погрешность для
него будет порядка
,
где n
порядок метода (так как здесь мы
рассматриваем метод РунгеКутта
четвертого порядка, погрешность для
него будет порядка
![]() ),
хотя точных способов оценки погрешности
нет, и это является недостатком метода.
Для грубой оценки погрешности метода
применяют так называемый принцип
Рунге [5].
Согласно Рунге, величину погрешности
вычисляют при помощи двойного счета
),
хотя точных способов оценки погрешности
нет, и это является недостатком метода.
Для грубой оценки погрешности метода
применяют так называемый принцип
Рунге [5].
Согласно Рунге, величину погрешности
вычисляют при помощи двойного счета
![]() ,
(3.60)
,
(3.60)
где
![]()
значение функции, вычисленное с шагом
h/2;
значение функции, вычисленное с шагом
h/2;
![]()
вычисленное значение с шагом h.
вычисленное значение с шагом h.
Отметим, метод
РунгеКутта
при
![]() не используется [13].
не используется [13].
В примерах на решение уравнений по методу РунгеКутта результаты будем представлять схемой, приведенной в табл. 9. Обозначения в таблице очевидны.
Пример 16. Методом РунгеКутта вычислить на отрезке [0; 0,5] интеграл дифференциального уравнения (примеры 8 и 15)
![]() ,
(3.61)
,
(3.61)
приняв шаг h = 0.1.
Таблица 9. Схема метода РунгеКутта
-
i
x
y
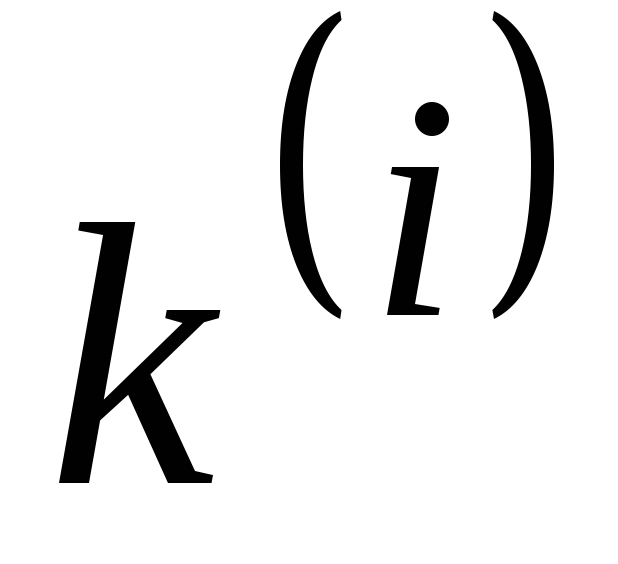
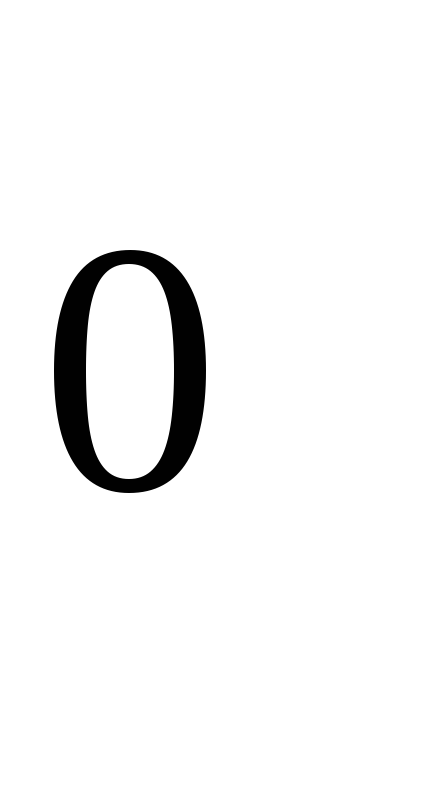
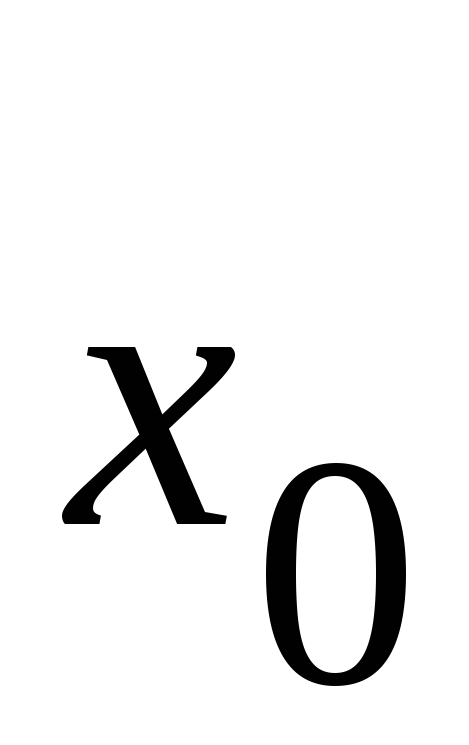
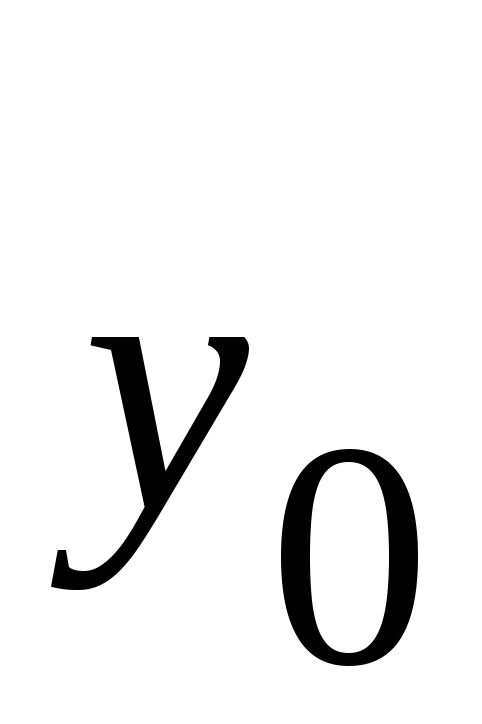
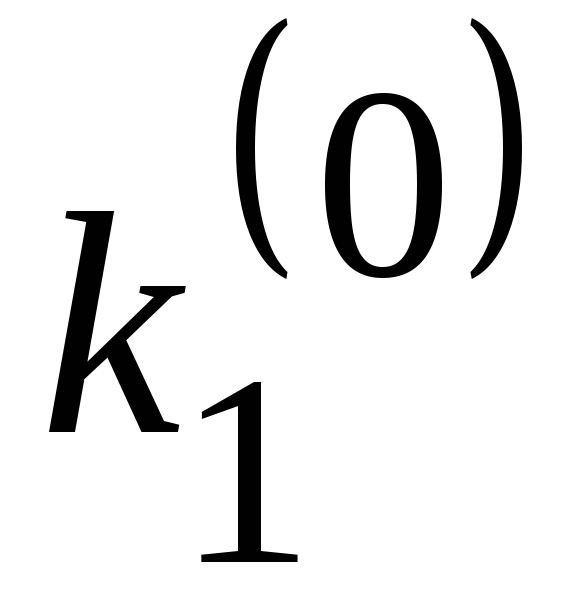
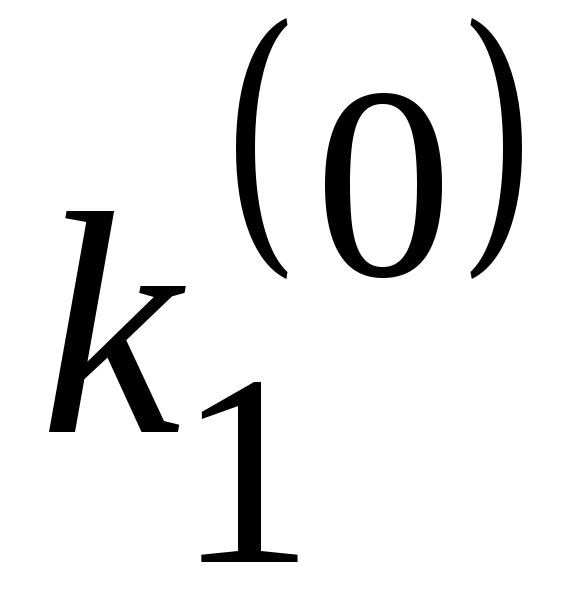
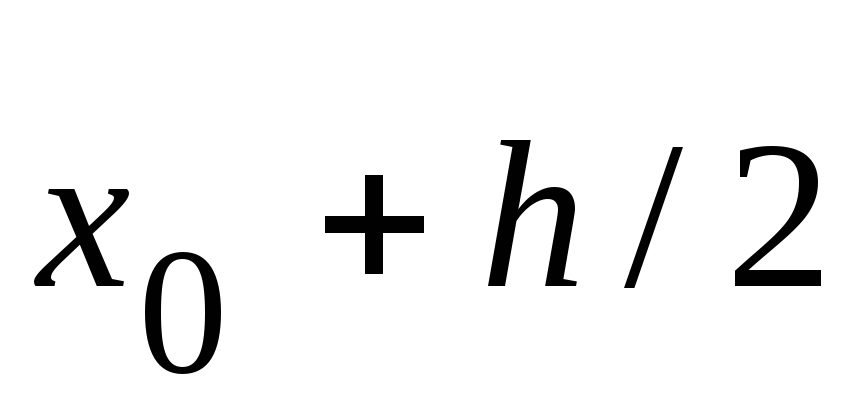
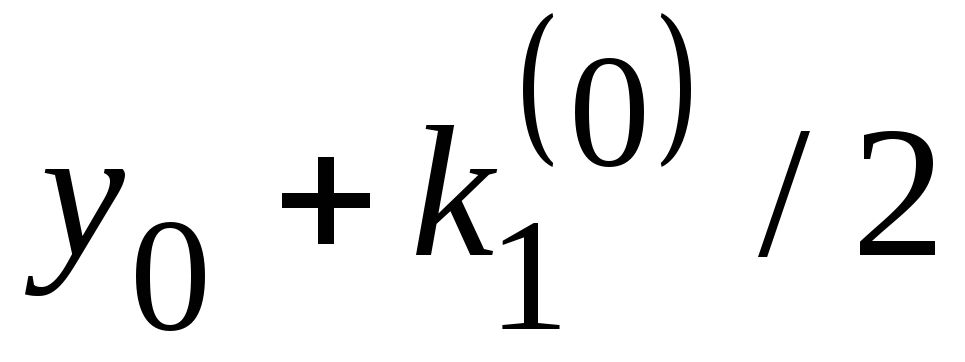
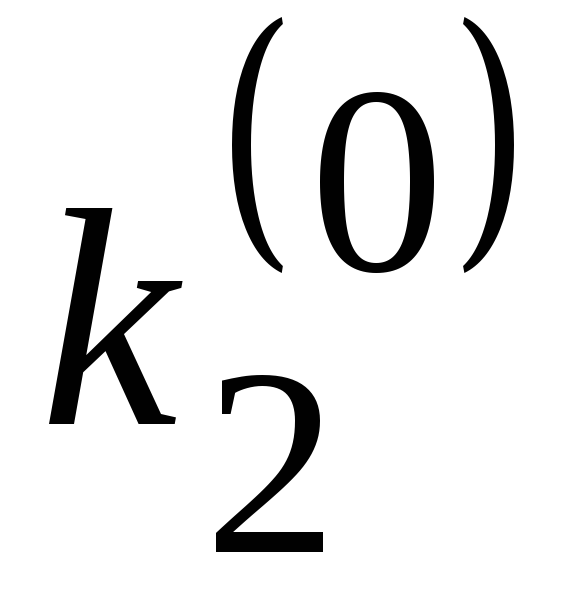
2
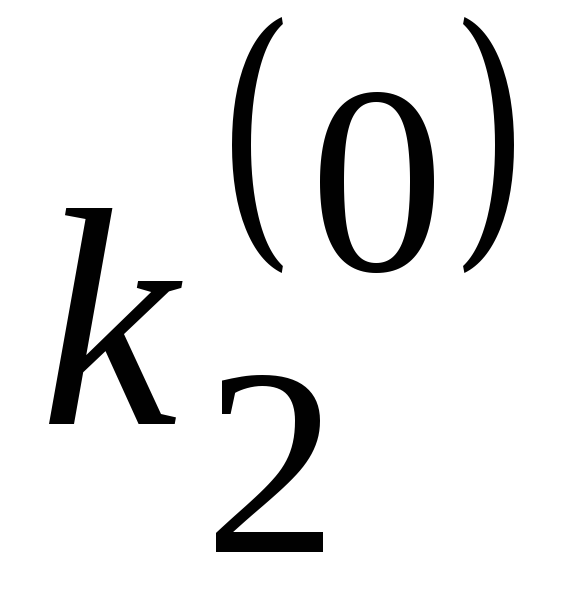
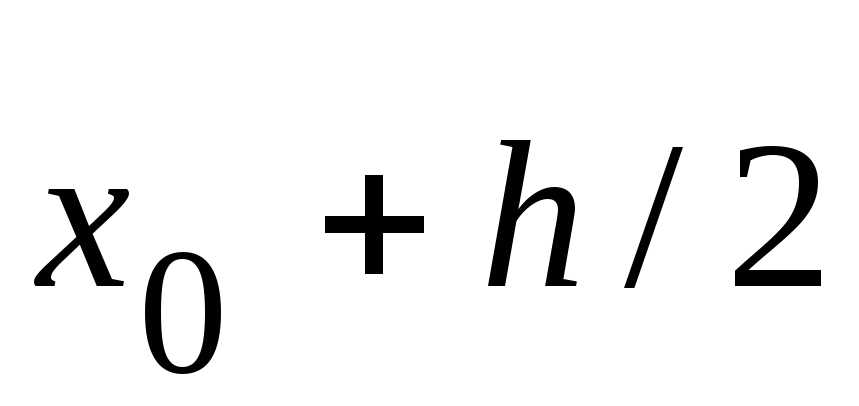
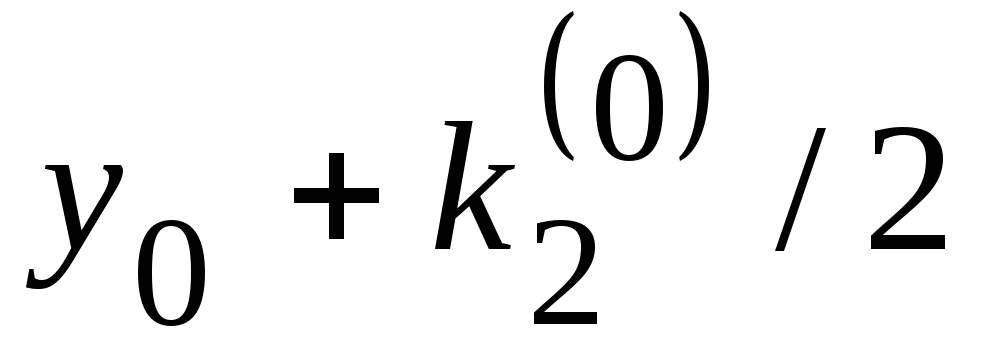
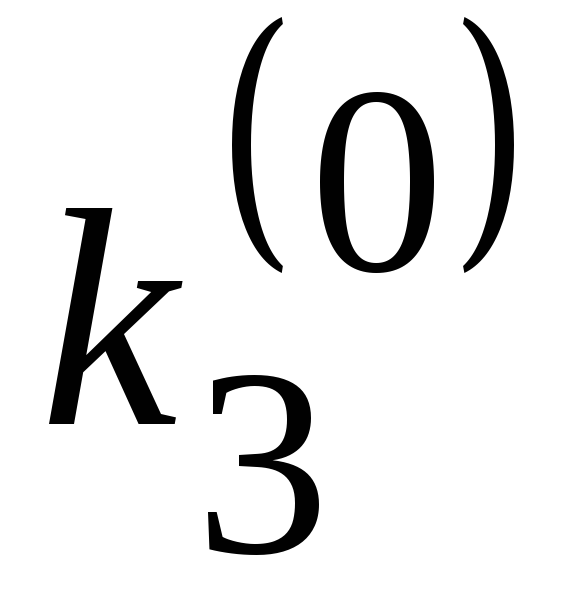
2
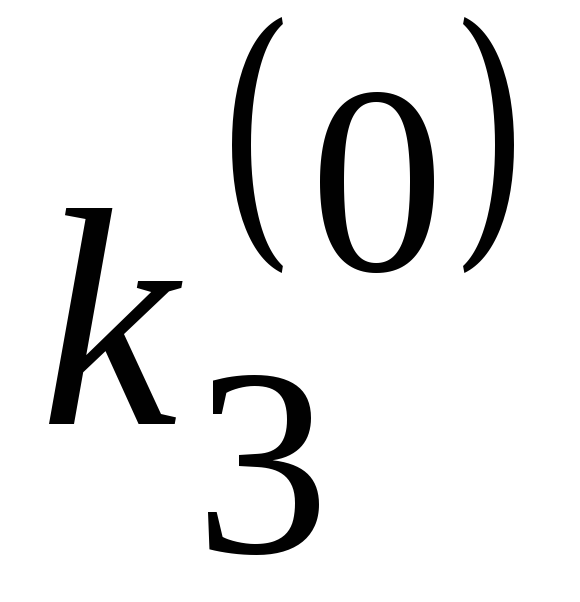
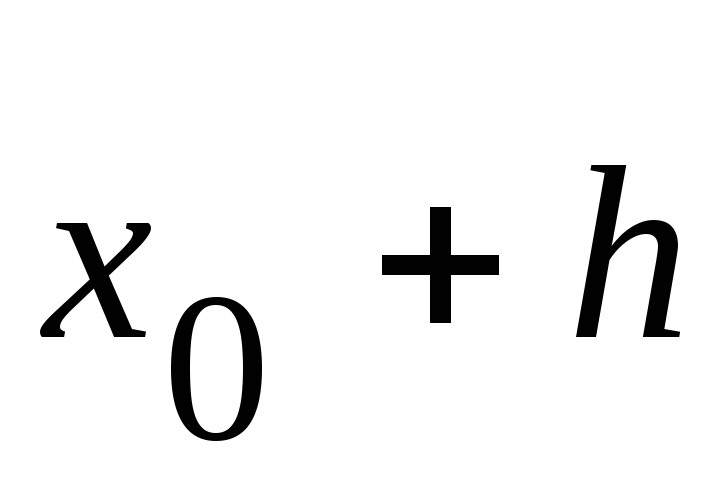
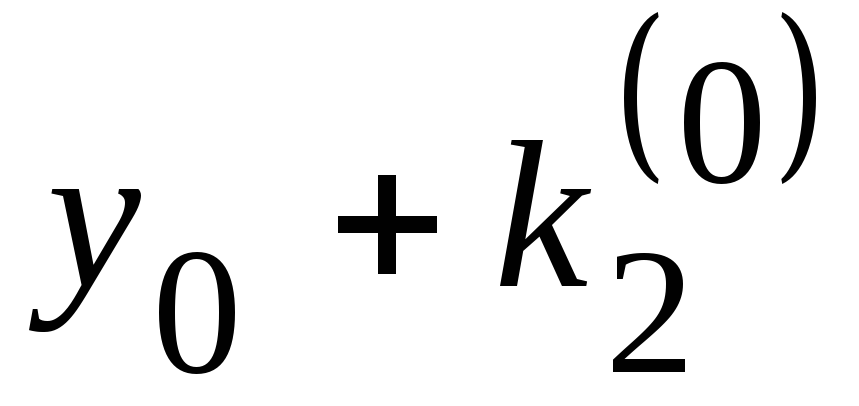
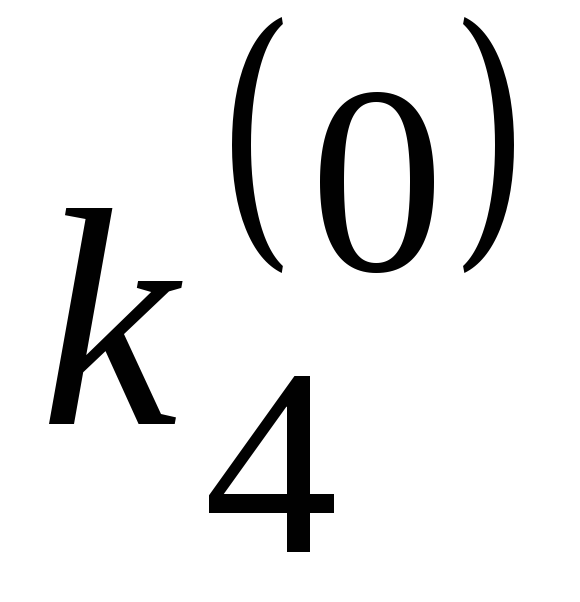
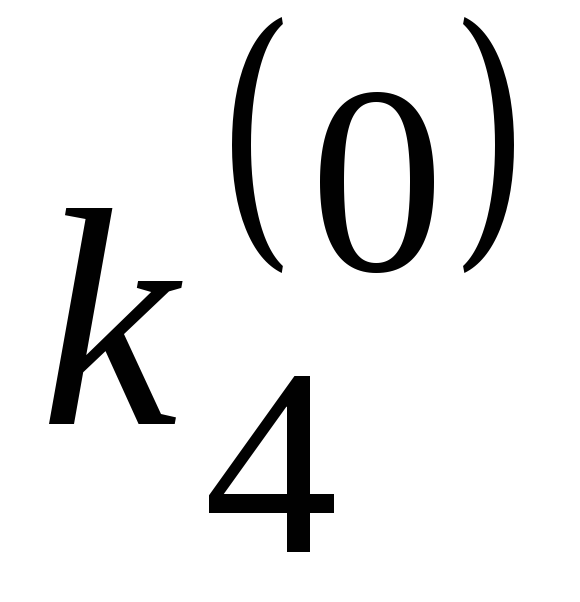
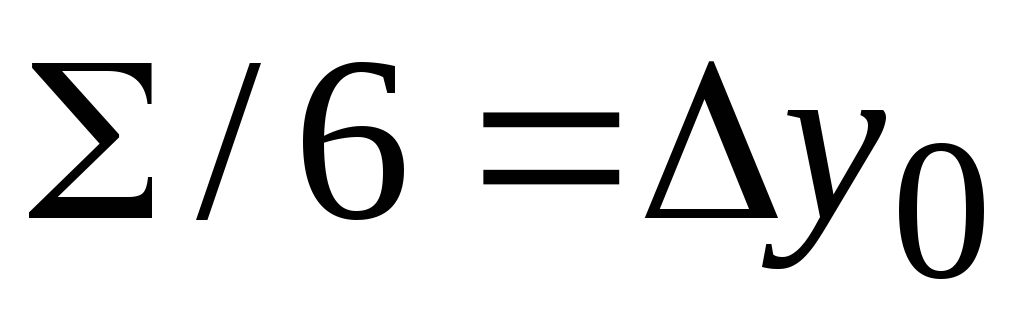
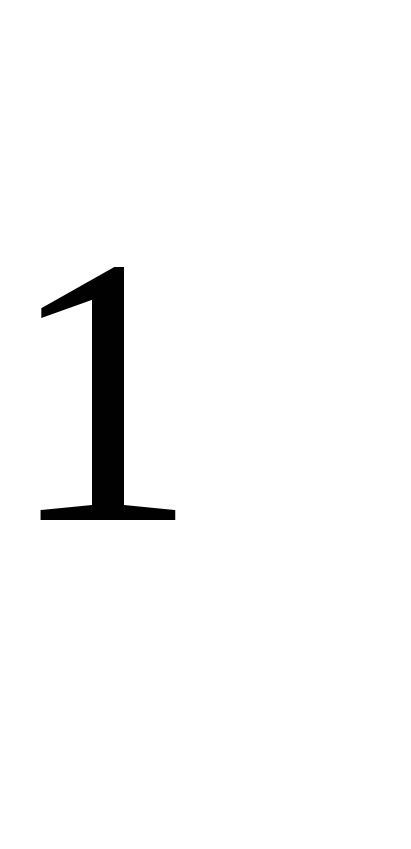
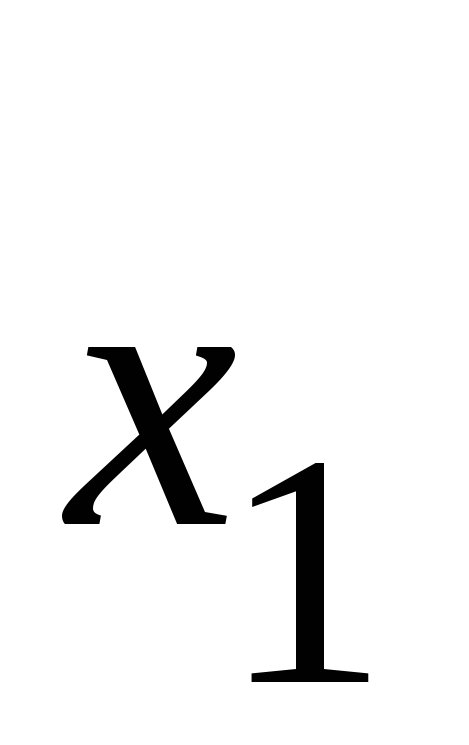
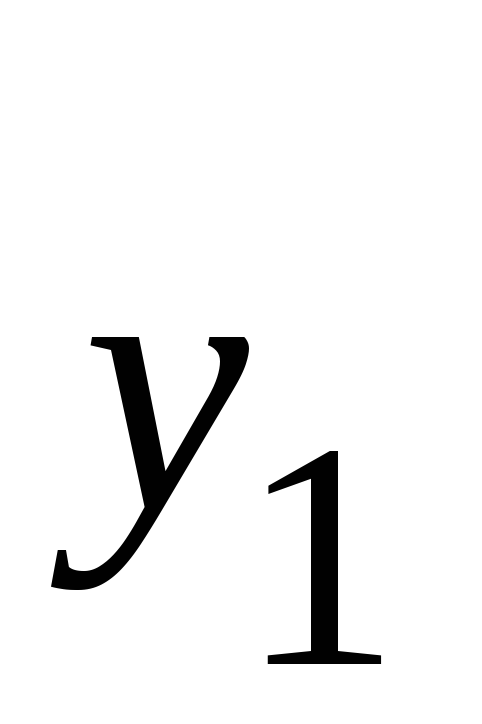
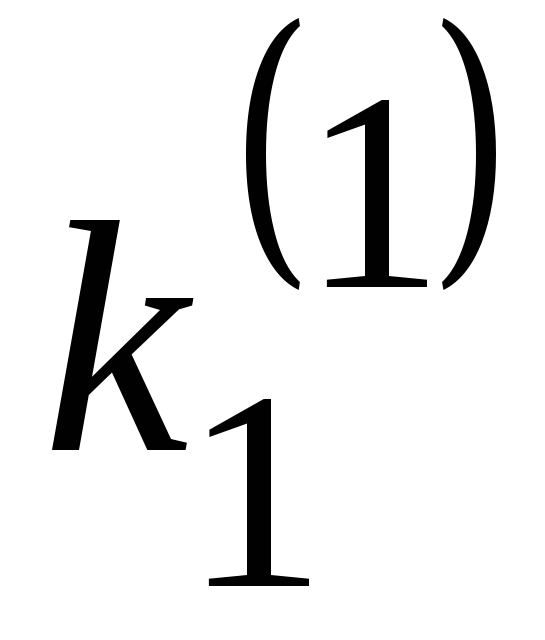
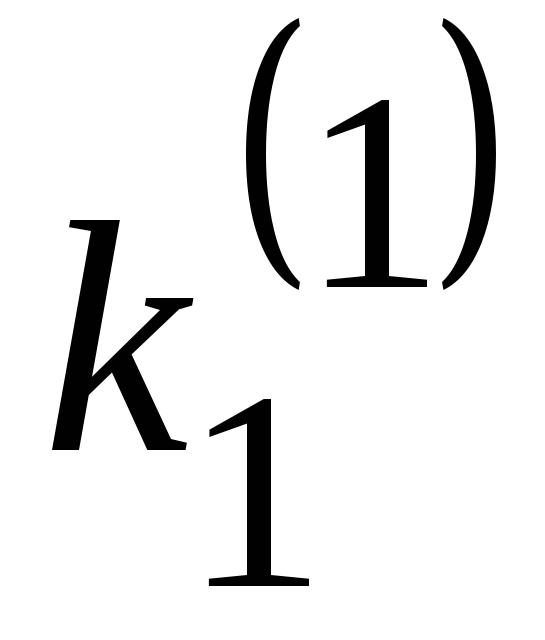





Решение. Покажем начало процесса.
Вычисление
![]() .
Последовательно имеем:
.
Последовательно имеем:
![]() ,
,
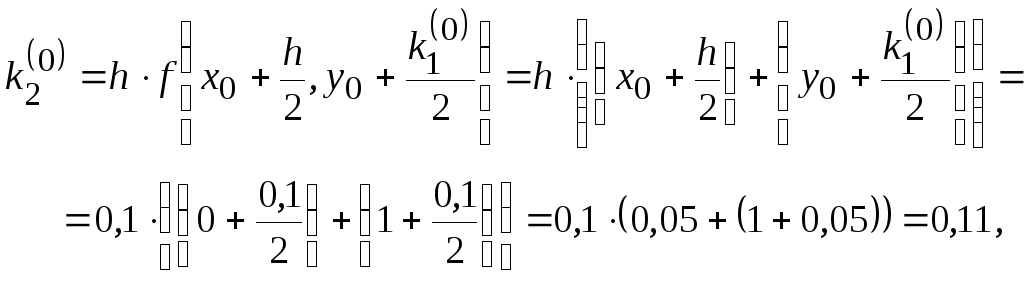
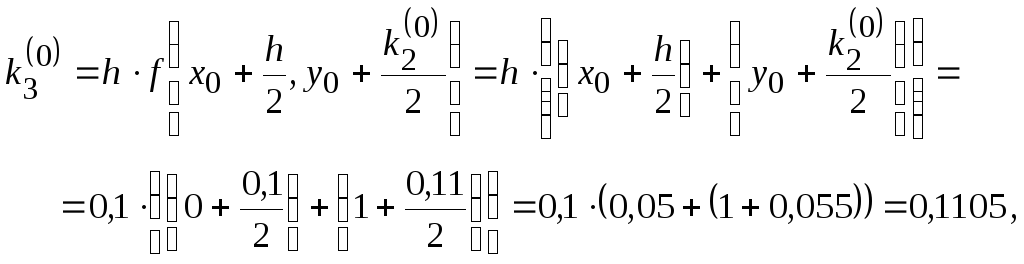
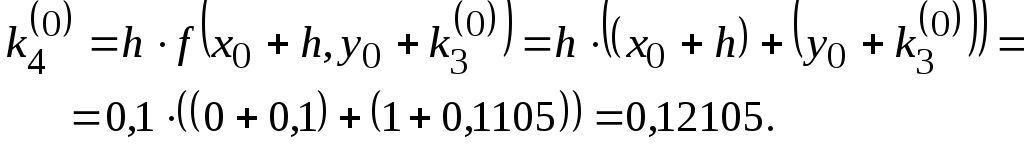
Отсюда
![]() ,
,
и, следовательно,
![]() .
.
Аналогично вычисляются
дальнейшие приближения. Результаты
вычислений приведены в табл. 10 (искомые
значения функции выделены жирным
шрифтом). Таким образом,
![]() .
Уравнение (3.61) имеет точное решение
.
Уравнение (3.61) имеет точное решение
![]() ,
откуда
,
откуда
![]()
Метод РунгеКутта применим для приближенного решения систем обыкновенных дифференциальных уравнений.
