
- •Введение
- •Основные макроэкономические понятия §1. Макро- и микротеория. Агрегирование
- •§2. Факторы производства
- •§3. Износ. Амортизация и инвестиции
- •§4. Измерение объёма национального производства и национального дохода
- •§5. Сбережения и норма процента. Дисконтирование
- •§6. Ценные бумаги
- •Облигации
- •§7. Денежная масса, номинальная и реальная заработная плата
- •§8. Международная торговля и системы валютных курсов
- •§ 9. Производственная функция
- •§10. Список основных макроэкономических элементов
- •Классическая теория §1. Макроэкономические теории
- •§2. Рынок труда
- •Предложение труда
- •Спрос на труд
- •Равновесие на рынке труда
- •§3. Рынок капитала (сбережений и инвестиций)
- •Предложение капитала
- •Спрос на капитал
- •Равновесие на рынке капитала
- •§4.Денежный рынок
- •§5 Краткий обзор классической теории
- •§6 Сравнительная статика
- •§7 Критика классической теории
- •Теория Кейнса
- •§1 Склонность к потреблению
- •§2 Спекулятивный спрос на деньги
- •§3 Рынок труда
- •§4 Рынок капитала (сбережений и инвестиций)
- •§5 Денежный рынок
- •§6 Краткая формулировка модели и определение равновесия
- •§7 Существование и единственность равновесия в модели Кейнса
- •§8 Инфляция и безработица
- •§9 Сравнительная статика. Изменение предложения денег.
- •§10 Сравнительная статика. Изменение производственной функции.
- •§11 Сравнительная статика. Изменение номинальной зарплаты
- •Экономический рост §1 Однопродуктовая макроэкономическая модель
- •§2 Независимость производственного процесса от масштаба
- •§3 Модель Солоу
- •§4 Сбалансированный рост
- •§5 Асимптотическое поведение траектории в модели Солоу
- •§6 Оптимальная норма накопления
- •§ 7 Была ли необходима перестройка экономики в ссср?
- •Элементы теории потребительского поведения §1. Отношение предпочтения и функция полезности
- •§2. Неоклассическая задача потребления
- •Теория фирм
- •§1 Задача максимизации прибыли фирмы в условиях совершенной конкуренции
- •§2 Несовершенная конкуренция. Монополия и монопсония
- •§3 Конкуренция среди немногих. Олигополия, олигопсония
Теория фирм
Одним из основных понятий макроэкономической теории является фирма, определяемая, как некоторая организация, производящая затраты экономических факторов таких как земля, труд и капитал, для изготовления продукции и услуг, которые она продает или предоставляет потребителям или другим фирмам.
§1 Задача максимизации прибыли фирмы в условиях совершенной конкуренции
Неоклассическая теория
фирмы построена на предположении, что
цель фирмы заключается в максимизации
прибыли путём выбора видов затрат
(ресурсов). Будем считать, что известна
производственная функция фирмы
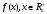 ,
значения которой в данном случае
представляют собой годовой физический
объём выпускаемой продукции. Кроме того
предполагаются заданными цена
,
значения которой в данном случае
представляют собой годовой физический
объём выпускаемой продукции. Кроме того
предполагаются заданными цена
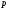 продукции и вектор цен
продукции и вектор цен
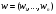 ,
используемых при производстве ресурсов.
Прибыль
,
используемых при производстве ресурсов.
Прибыль
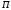 равна годовому доходу
равна годовому доходу
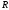 за вычетом издержек производства
за вычетом издержек производства
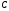 :
:
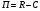 .
Годовой доход равен произведению
физического объёма выпущенной за год
продукции на её цену:
.
Годовой доход равен произведению
физического объёма выпущенной за год
продукции на её цену:
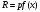 .
Издержки производства равны общим
выплатам за все ресурсы:
.
Издержки производства равны общим
выплатам за все ресурсы:
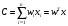 .
Предполагается, что фирма способна
делать любые затраты, то есть выбирать
любую точку из пространства ресурсов
.
Предполагается, что фирма способна
делать любые затраты, то есть выбирать
любую точку из пространства ресурсов
 .
Тогда задача максимизации прибыли фирмы
формулируется следующим образом:
.
Тогда задача максимизации прибыли фирмы
формулируется следующим образом:
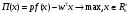 (1)
(1)
Это наиболее простая
модель задачи о максимизации прибыли.
В ней не учитывается ряд факторов,
например, то обстоятельство, что затраты
не могут быть сколь угодно большими. И
капитал, и ресурсы – величины ограниченные.
Для того, чтобы модель адекватно описывала
реальную ситуацию, в ней должны быть
ограничения вида
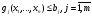 ,
или в векторной форме
,
или в векторной форме
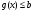 .
К таким ограничениям, в частности,
относятся бюджетные ограничения
.
К таким ограничениям, в частности,
относятся бюджетные ограничения
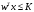 ,
где К – бюджет фирмы, то есть
количество денег в её распоряжении.
,
где К – бюджет фирмы, то есть
количество денег в её распоряжении.
Из сказанного, однако, не следует, что бессмысленно ставить задачу в виде (1). Эта задача также решает вопрос о максимальной прибыли, если оптимальные затраты в ней доступны фирме.
Предположим, что решение
задачи (1) существует, и пусть
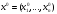 – вектор оптимальных затрат. Если при
некотором
– вектор оптимальных затрат. Если при
некотором
 имеет место неравенство
имеет место неравенство
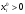 ,
то функция одной переменной
,
то функция одной переменной
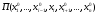 будет иметь в точке локальный максимум,
поэтому
будет иметь в точке локальный максимум,
поэтому
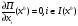 (2)
(2)
Соотношение (2) можно записать в виде
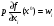 (3)
(3)
или
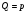 ,
,
где
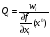 (4)
(4)
Соотношение (3) означает,
что на оптимальном плане производства
предельные производительности
используемых ресурсов пропорциональны
их ценам с коэффициентом пропорциональности
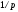 .
.
Величина
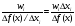 ,
где
,
где
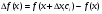 характеризует стоимость дополнительных
затрат
характеризует стоимость дополнительных
затрат
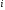 -го
вида, связанных с производством еще
одной единицы продукции. В связи с этим
-го
вида, связанных с производством еще
одной единицы продукции. В связи с этим
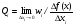 называют предельными издержками
производства по
называют предельными издержками
производства по
 -му
ресурсу. Как видно из (4), на оптимальном
плане производства предельные издержки
по всем используемым ресурсам
совпадают и равны цене выпускаемой
продукции. Связь между ценами и издержками
с точки зрения производителя очевидна.
Некоторые экономисты, становясь на
позиции производителя, пытались
трактовать формулу (4) таким образом,
что цена определяется лишь издержками
производства. Однако это так же
неубедительно, как и то, что цены
определяются лишь полезностью товаров
(см. §5.2). При выводе формулы (4) предполагалось,
что цены уже заданы. Один изолированный
производитель не может определять цены,
если только он не монополист.
-му
ресурсу. Как видно из (4), на оптимальном
плане производства предельные издержки
по всем используемым ресурсам
совпадают и равны цене выпускаемой
продукции. Связь между ценами и издержками
с точки зрения производителя очевидна.
Некоторые экономисты, становясь на
позиции производителя, пытались
трактовать формулу (4) таким образом,
что цена определяется лишь издержками
производства. Однако это так же
неубедительно, как и то, что цены
определяются лишь полезностью товаров
(см. §5.2). При выводе формулы (4) предполагалось,
что цены уже заданы. Один изолированный
производитель не может определять цены,
если только он не монополист.
