44. Неравенство с модулем

Основные способы решений неравенств с модулем во многом совпадают с методами решения аналогичных уравнений. Единственное отличие, пожалуй, связано с тем, что, решая неравенства с модулем (как, впрочем, и неравенства вообще), нужно очень внимательно совершать равносильные переходы и следить не только за тем, чтобы не приобрести новые решения, но и за тем, чтобы не потерять уже имеющиеся.

Стандартный путь решения неравенств с модулем заключается в том, что координатная прямая разбивается на промежутки (границами этих промежутков являются нули подмодульных выражений), а затем неравенство решается на каждом из промежутков.

Этот метод работает всегда. Правда, в отдельных случаях может быть затруднена его техническая реализация, например, очень тяжело или невозможно найти корни подмодульных выражений и пр. Однако, это сложности иного плана. Нужно понимать, что раскрытие модуля по определению неизменно приводит к цели. Конечно же, этот метод не является оптимальным: в условиях конкурсного экзамена важен не только результат, но и то время, которое потрачено на его получение.

Рассмотрим методы, не связанные с поиском нулей функций, стоящих под знаком модуля.

Рассмотрим неравенство Очевидно, что те x , для которых g  ( x ) < 0, не являются решениями. Значит, если x является решением, то для него g  ( x ) ≥ 0, и согласно геометрическому смыслу модуля, как расстоянию на координатной оси, данное неравенство равносильно системе Таким образом, имеем

Аналогично можно рассмотреть неравенство Неравенство выполнено для тех x , для которых g  ( x ) < 0 и функции f  ( x ) и g  ( x ) определены. Для тех x , для которых g  ( x ) ≥ 0, имеем равносильную совокупность

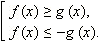
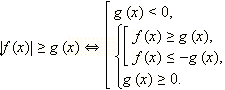
Заметим, что последняя совокупность является равносильной нашему неравенству и при g  ( x ) ≤ 0. В этом можно непосредственно убедиться, учтя g  ( x ) ≤ 0 и вспомнив

45. Числовые последовательности, виды

Понятие последовательности

Последовательностью элементов множества E называется отображение

т. е. функция, которая каждому натуральному числу ставит в соответствие элемент .

Для записи последовательности употребляем обозначения (x_n), или x₁, x₂, ..., x_n, ..., или x_n = f(n), .

Элементы x₁, x₂, ..., x_n, ... называются членами последовательности, а x_n - общим членом последовательности.

Множество E может быть различным, например: R, R^m, C[a, b], и т.д. Если E = R, то последовательность называется числовой, если E = R^m, - векторной, если E = C[a, b], - функциональной, если E = - матричной и т. д. В каждом из этих случаев множество всевозможных последовательностей образует векторное нормированное, а следовательно, и метрическое пространство.

Сходящиеся последовательности и их свойства

Рассмотрим числовые последовательности.

Последовательность (x_n) действительных чисел называется сходящейся, если существует действительное число a и для произвольного ε > 0 существует натуральное число m такое, что для всех n > m справедливо неравенство |x_n - a| < ε.

При этом число a называют пределом последовательности (x_n), что символически записывают

или x_n → a при n → ∞.