154. Возвышение в квадрат произведения, степени и дроби.

а) Пусть требуется возвысить в квадрат произведение нескольких сомножителей, напр.    аbс. Это значит, что требуется аbс умножить на аbс. Но чтобы умножить на произведение аbс, можно умножить множимое на а, результат умножить на b и что получатся умножить еще на с .

Значит:

(аbс)² = (аbс) (аbс) = (аbс) аbс = аbсаbс

(мы отбросили последние скобки, так как от этого смысл выражения не изменяется). Теперь, пользуясь сочетательным свойством умножения (отдел1§ 34, б), сгруппируем сомножители так:

(аа) (bb) (сс),

что можно сокращенно написать: а²b²с².

Значит, чтобы возвысить произведение в квадрат, можно возвысить в квадрат каждый сомножитель отдельно (Для сокращения речи правило это, как и последующее, выражено не полно; надо было бы еще добавить: „и полученные результаты перемножить". Добавление ото само собой подразумевается..)

Таким образом:

( ³/₄ xy)²  =  ⁹/₁₆  x² y²;    (— 0,5mn)² = + 0,25m²n²;    и т. п.

б)  Пусть требуется какую-нибудь  степень, напр. a³, возвысить в квадрат. Это можно выполнить так:

(а³)² = а³ • а³ = а³⁺³ = а⁶.

Подобно этому: (х⁴)² = x⁴ • x⁴ = x⁴⁺⁴ = x⁸

Значит, чтобы возвысить степень в квадрат, можно показатель степени умножить на 2.

Таким образом, применяя эти два правила, будем, напр., иметь:

(— 3 ³/₄  a x² y³)² = (— 3 ³/₄ )² a² (x²)² (у³)² = ²²⁵/₂ a² x⁴ y⁶

в)   Пусть   требуется   возвысить   в   квадрат   какую-нибудь дробь ^a/_b. Тогда, применяя правило  умножения дроби на дробь, получим:

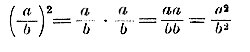
Значит,  чтобы возвысить в  квадрат дробь, можно возвысить в квадрат отдельно числитель и знаменатель.

Пример.

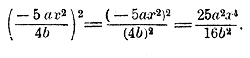
36. Логарифм

Логари́фм числа b по основанию a (от греч. λόγος — «слово», «отношение» и ἀριθμός — «число»^[1]) определяется как показатель степени, в которую надо возвести основание a, чтобы получить число b. Обозначение: . Из определения следует, что записи и равносильны.

Например, , потому что .

38. Степенная функция

Степенной функцией с вещественным показателем a называется функция y = x ⁿ , x > 0.

Заметим, что для натуральных n степенная функция определена на всей числовой оси. Для произвольных вещественных n это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x .

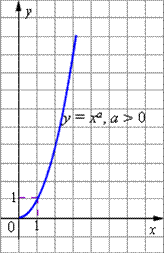
К основным свойствам степенной функции y = x ^a при a > 0 относятся:

• Область определения функции - промежуток (0; + ).

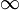• Область значений функции - промежуток (0; +).

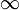• Для любых a график функции проходит через точку (1; 1).

• Функция строго монотонно возрастает в области определения функции, то есть, если x₁ < x₂ то a^r₁ < a^r₂ .

• График степенной функции при a > 0 изображен на рисунке.

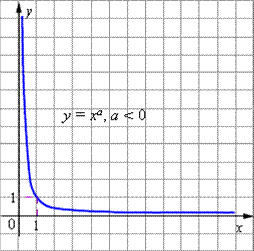
К основным свойствам степенной функции y = x ^a при a < 0 относятся:

• Область определения функции - промежуток (0; +).

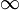• Область значений функции - промежуток (0; +).

• Для любых a график функции проходит через точку (1; 1).

• Функция строго монотонно возрастает в области определения функции, то есть, если x₁ < x₂ то a^r₁ > a^r₂ .

• График степенной функции при a < 0 изображен на рисунке.

Справедливы следующие свойства степенной функции:

• x^a₁x^a₂ = x^a₁ ^{+ a}₂

• x^a₁ : x^a₂ = x^a₁ ^{- a}₂

• (x^a₁)^a₂ = x^a₁ ^a₂

• x^a₁ > x^a₂, x > 1, a₁ > a₂

• x^a₁ < x^a₂, 0 < x < 1, a₁ < a₂

39. Обратная функция

Функция является обратной к функции , если выполнены следующие тождества:

• f(g(y)) = y для всех

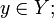
• g(f(x)) = x для всех

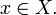
Чтобы найти обратную функцию, нужно решить уравнение x = F(y) относительно y. Если оно имеет более чем один корень, то функции обратной к F не существует. Таким образом, функция f(x) обратима на интервале (a;b) тогда и только тогда, когда на этом интервале она инъективна.

Для непрерывной функции F(y) выразить y из уравнения x − F(y) = 0 возможно в том и только том случае, когда функция F(y) монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её монотонности. Например, является обратной функцией к x² на , хотя на промежутке обратная функция другая: .