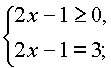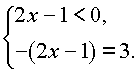42. Квадратные неравенства
Определение. Квадратным неравенством называется неравенство вида ax2 + bx + c > 0, где вместо знака > может быть другой знак неравенства: , < или .
Для решения квадратного неравенства надо представить себе расположение графика функции y = ax2 + bx + c относительно оси Ox. Возможны два основных случая – график совсем не пересекает ось Ox (трехчлен не имеет корней) или пересекает ее в двух точках (трехчлен имеет два корня). Исключительный случай, когда график касается оси Ox (трехчлен имеет один корень) мы рассмотрим отдельно.
Рассмотрим сначала случай, когда график не пересекает оси Ox. В этом случае квадратичная функция сохраняет постоянный знак на всей числовой оси, причем этот знак совпадает со знаком старшего коэффициента а. Поэтому решением квадратного неравенства в этом случае будут либо все вещественные числа, либо пустое множество (не будет решений вовсе).
Теперь рассмотрим случай, когда график квадратичной функции пересекает ось Ox в двух точках, то есть когда квадратное уравнение ax2 + bx + c = 0 имеет два корня x1 и x2 (x1 < x2).
В этом случае функция y = ax2 + bx + c между корнями, то есть в промежутке (x1; x2) сохраняет один знак (а именно, знак, противоположный знаку а), а “вне корней”, то есть на двух промежутках (– ; x1) и (x2; + ) имеет противоположный знак (сейчас он совпадает со знаком старшего коэффициента).
Случай,
когда график квадратичной функции
касается оси Ox,
то есть когда уравнение ax2 + bx + c = 0
имеет единственный корень, на самом
деле, мало отличается от первого случая,
когда корней совсем нет. Действительно,
в этом случае квадратичная функция
сохраняет постоянный знак во всех
точках, кроме единственной – точки
x = –
,
где она обращается в нуль. При записи
ответа надо не забыть учесть эту
исключительную точку x = –
.
Составим алгоритм решения квадратного неравенства, в левой части которого стоит квадратичная функция y = f(x), где f(x) = ax2 + bx + c, а само неравенство имеет один из четырех видов: y > 0, y 0, y < 0 или y 0.
1. Определяем, сколько корней имеет трехчлен ax2 + bx + c. Это можно сделать по знаку его дискриминанта D = b2 – 4ac:
а) D > 0 два корня,
б) D < 0 нет корней,
в) D = 0 один корень.
2. В
случаях б) и в) сразу записываем ответ.
Он может выглядеть так: R
(решениями являются все числа);
(решений нет); x = –
(неравенство выполняется в единственной
точке).
3. В случае а) находим корни x1 и x2 (x1 < x2) и записываем ответ. Он может выглядеть для строгих неравенств так: (– ; x1) (x2; + ); (x1; x2).
В случае нестрогого неравенства в ответ надо включить точки x1 и x2: (– ; x1] [x2; + ); [x1; x2].
43. Уравнение содержащие переменную под знаком модуля
При решении таких уравнений применяют чаще всего следующие методы: а) раскрытие модуля; b) возведение обеих частей уравнения в квадрат; с) разбиение на промежутки.
Пример 2.4.1. Решить уравнение
Решение
а) Так как по определению
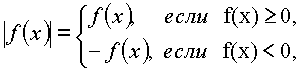
то исходное уравнение равносильно следующей совокупности двух смешанных систем:
|
|
|
Из первой системы этой совокупности находим x = 2, а из второй x = –1.
b) Так как обе части исходного уравнения – выражения одинаковых знаков, то оно равносильно следующему уравнению:
|
|
или |
|
Решая последнее уравнение, находим те же корни.
Ответ: –1; 2.