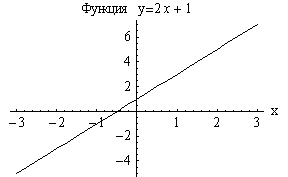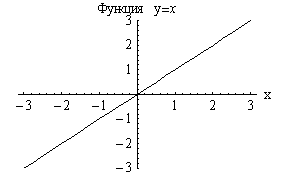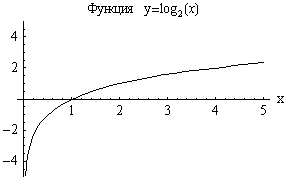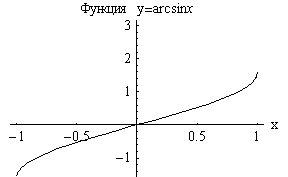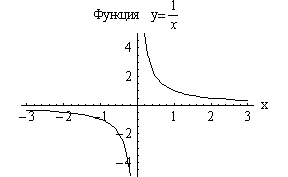Действия над векторами, заданными своими координатами
|
Сложение |
Вычитание |
Умножение |
|
При сложении векторов их соответстветственные координаты складываются. |
При вычитании векторов их соответстветственные координаты вычитаются. |
При умножении вектора на число все его координаты умножаются на это число |
19. Определение длины вектора, расстояние между двумя точками на плоскости
Вектором называеься направленный отрезок(отрезок,у которого одна граничная точка считается начальной, другая - конечной). Над буквенным обозначением вектора ставится стрелка. Длиной вектора называеттся расстояние между началом и концом вектора. Нулевым называется вектор,у которого начало и конец равны нулю. Его направление не определено. Два ненулевых вектора, лежащих на одной прямой или на параллельных прямых, называются коллинеарными. Нулевой коллинеарен любому вектору. Вектор, длина которого равна единице,называется единичным вектором. Векторы называют равными,если они коллинеарны,имеют одинаковую длину и направление. Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если тройка векторов содержит нулевой вектор или пару коллинеарных векторов,то эти векторы компланарны. Векторы называют противоположными, если их длины равны,а направления противоположны.
20. Как делятся отрезки в данном соотношении
Если
точка М(x;
y)
лежит на прямой, проходящей через две
данные точки
(
,
)
и
(
,
),
и дано отношение
,
в котором точка М делит отрезок
,
то координаты точки М определяются по
формулам
,
Если
точка М является серединой отрезка
,
то ее координаты определяются по формулам
,
.
21.Уравнение прямой, прох. Через точку.
. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
Пример.
Найти уравнение прямой, проходящей
через точку А(1, 2) перпендикулярно вектору
(3,
-1).
Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А.
Получаем: 3 – 2 + C = 0, следовательно С = -1.
Итого: искомое уравнение: 3х – у – 1 = 0.
Общее уравнение прямой:
Ах + Ву + С = 0 ,
где А и В не равны нулю одновременно.
Коэффициенты А и В являются координатами нормального вектора прямой ( т.е. вектора, перпендикулярного прямой ). При А = 0 прямая параллельна оси ОХ , при В = 0 прямая параллельна оси ОY .
При
В
0
получаем
уравнение
прямой с угловым коэффициентом:
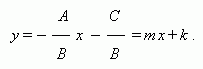
Уравнение прямой, проходящей через точку ( х0 , у 0 ) и не параллельной оси OY, имеет вид:
у – у 0 = m ( x – х0 ) ,
где m – угловой коэффициент, равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ .
При
А
0,
В
0
и С
0
получаем
уравнение
прямой в отрезках на осях:
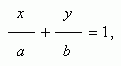
где a = – C / A , b = – C / B . Эта прямая проходит через точки ( a, 0 ) и ( 0, b ), т.е. отсекает на осях координат отрезки длиной
23. Уравнение прямой через точку и имеющую направл. Вектор
Определение.
Каждый
ненулевой вектор
(
α1
, α2
), компоненты которого удовлетворяют
условию А α1
+ В α2
= 0 называется направляющим вектором
прямой
Ах + Ву + С = 0.
Пример.
Найти уравнение прямой с направляющим
вектором
(1,
-1) и проходящей через точку А(1, 2).
Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.
при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:
х + у - 3 = 0
24. Уравнение прямой ч.з две точки
Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой, проходящей через эти точки:
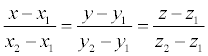
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.
На плоскости записанное выше уравнение прямой упрощается:
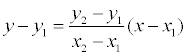
если х 1 ≠ х2 и х = х 1 , если х 1 = х2 .
Дробь
=
k называется угловым
коэффициентом прямой.
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Применяя записанную выше формулу, получаем:
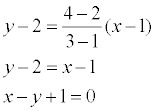
25. Уравнение прямой в отрезках
Если
в общем уравнении прямой Ах + Ву + С = 0
С≠0, то, разделив на –С, получим:
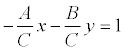или
,
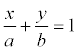где
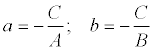
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
С
= 1,
,
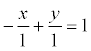а = -1, b = 1.
26. Определение окружности
|
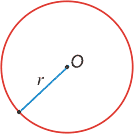
Определения: Окружностью называется фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки. Эта точка (О) называется центром окружности. Расстояние (r) от точки окружности до ее центра называется радиусом окружности. Радиусом называется также любой отрезок, соединяющий точку окружности с ее центром. Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром (d=2r).
Касательная — прямая (а), проходящая через точку (А) окружности перпендикулярно к радиусу, проведенному в эту точку, называется. При этом данная точка (А) окружности называется точкой касания.
Часть плоскости, ограниченная окружностью, называется кругом. |
|
30. Определение системы двух линейных уравнений с 2 переменными
Системы двух линейных уравнений с двумя неизвестными имеют вид:
где a, b, c, d, e, f – заданные числа; x, y – неизвестные. Числа a, b, d, e – коэффициенты при неизвестных; c, f – свободные члены. Решение этой системы уравнений может быть найдено двумя основными методами.
Метод подстановки.
1) Из одного уравнения выражаем одно из неизвестных, например x, через коэффициенты и другое неизвестное y:
x = ( c – by ) / a . (2)
2) Подставляем во второе уравнение вместо x :
d ( c – by ) / a + ey = f .
3) Решая последнее уравнение, находим y :
y = ( af – cd ) / ( ae – bd ).
4) Подставляем это значение вместо y в выражение (2) :
x = ( ce – bf ) / ( ae – bd ) .
П р и м е р . Решить систему уравнений:
Из первого уравнения выразим х через коэффициенты и y :
x = ( 2y + 4 ) / 3 .
Подставляем это выражение во второе уравнение и находим y :
( 2y + 4 ) / 3 + 3y = 5 , откуда y = 1 .
Теперь находим х, подставляя найденное значение вместо y в
выражение для х: x = ( 2 · 1 + 4 ) / 3, откуда x = 2 .
Сложение или вычитание. Этот метод состоит в следующем.
1) Умножаем обе части 1-го уравнения системы (1) на (– d ), а обе части 2-го уравнения на а и складываем их:
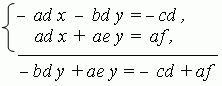
Отсюда получаем: y = ( af – cd ) / ( ae – bd ).
2) Подставляем найденное для y значение в любое уравнение системы (1):
ax + b( af – cd ) / ( ae – bd ) = c.
3) Находим другое неизвестное: x = ( ce – bf ) / ( ae – bd ).
П р и м е р . Решить систему уравнений:
методом сложения или вычитания.
Умножаем первое уравнение на –1, второе – на 3 и складываем их:
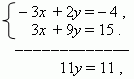
отсюда y = 1. Подставляем это значение во второе уравнение
(а в первое можно?): 3x + 9 = 15, отсюда x = 2.
Определители второго порядка. Мы видели, что формулы для решения системы двух линейных уравнений с двумя неизвестными имеют вид:
x = ( ce – bf ) / ( ae – bd ) ,
(3)
y = ( af – cd ) / ( ae – bd ) .
Эти формулы легко запоминаются, если ввести для их числителей и знаменателей следующий символ:
,
который
будет обозначать выражение: ps
– qr
.
Это выражение получается перекрёстным умножением чисел p, q, r, s :
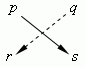
и последующим вычитанием одного произведения из другого: ps – qr. Знак « + » берётся для произведения чисел, лежащих на диагонали, идущей из левого верхнего числа к правому нижнему; знак « – » - для другой диагонали, идущей из правого верхнего числа к левому нижнему. Например,
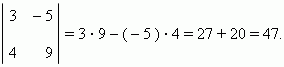Выражение
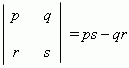называется
определителем
второго
порядка.
Правило Крамера. Используя определители, можно переписать формулы (3):
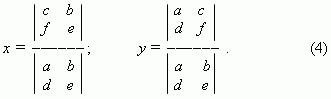
Формулы (4) называются правилом Крамера для системы двух линейных уравнений с двумя неизвестными.
П р и м е р . Решить систему уравнений
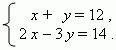
используя правило Крамера.
Р е ш е н и е . Здесь a = 1, b = 1, c = 12, d = 2, e = –3, f = 14 .
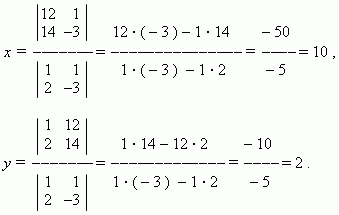
31. Определение системы 3 линейных ур-й с тремя уравнениями
Система трех линейных уравнений с тремя неизвестными
Система трех линейных уравнений с тремя неизвестными имеет вид
(7)
Определитель
(8)
составленный из коэффициентов при неизвестных, называется определителем системы.
1.
Если определитель системы
,
то система (7) имеет решение, и притом
единственное. Это решение находится по
формулам
(9)
Из этого заключаем, что значение неизвестного системы (7) равно дроби, знаменатель которой есть определитель системы, а числитель есть определитель, получающийся из определителя системы заменой в нем столбца из коэффициентов при определяемом неизвестном столбцом свободных членов.
Определители, стоящие в числителях дробей (9), будем обозначать соответственно через Dx, Dy, Dz.
2. Если D = 0, но, по крайней мере, один из его миноров и хотя бы один из определителей Dx, Dy и Dz не равен нулю, то система (7) решений не имеет. В этом случае говорят, что она противоречива, или несовместна.
3. Если D = 0 и все определители, стоящие в числителях дробей (9), - Dx, Dy, Dz - равны нулю, т. е. если
D = Dx = Dy = Dz = 0,
но хотя бы один из миноров в определителе D не равен нулю, то одно уравнение системы (7) является следствием двух других, и система трех уравнений (9) приводится к двум уравнениям, причем решения этих двух уравнений удовлетворяют третьему. В этом случае система (9) имеет бесконечное множество решений и называется неопределенной.
4. Если же все миноры в определителе D равны нулю, но хотя бы один из миноров в каком-нибудь из определителей Dx, Dy, Dz не равен нулю и хотя бы один из коэффициентов при неизвестных не равен нулю, то система несовместна и решений не имеет.
5. Если в определителях D, Dx, Dy, Dz все миноры равны нулю, но хотя бы один из коэффициентов при неизвестных нулю не равен, то два уравнения системы являются следствием третьего, и система трех уравнений приводится к одному уравнению, является неопределенной и имеет бесконечное множество решений, причем решения этого третьего уравнения удовлетворяют первому и второму уравнениям.
32. Определение функции примеры нахождения области определения
Определение. Функцией, заданной (или определенной) на некотором множестве X, называется соответствие, в силу которого любой элемент x множества X определяет некоторый (соответствующий ему) объект f(x).
Множество X называется областью определения функции, а множество Y - объектов, соответствующих всем элементам множества X, - областью значений функции
34. Элементарные функции
Графики элементарных функций
|
Все
графики |
|
Линейная
функция |
|
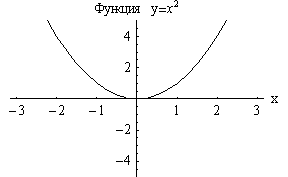
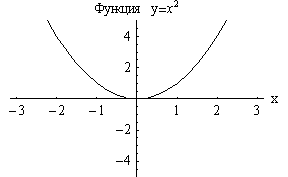
Квадратная
функция |
|
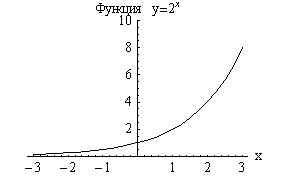
Показательная
функция |
|
Логарифмическая
функция |
|
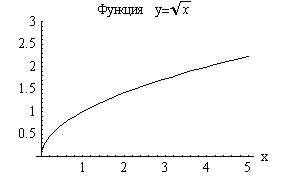
Функция
арифметический корень |
|
Степенная
функция |
|
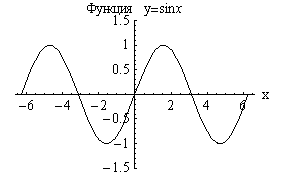
Тригонометрические
функции |
|
Обратные
тригонометрические функции |
|
Дробно-линейная
функция |
35. Определение степени числа
Определение степени. Напомним, что произведение двух одинаковых чисел аа называется второю степенью (или квадратом) числа а, произведение трех одинаковых чисел ааа называется третьей степенью (или кубом) числа а; вообще произведение n одинаковых чисел аа... а называется n-ю степенью числа а. Действие, посредством которого находится степень данного числа, называется возвышением в степень (вторую, третью и т. д.). Повторяющийся сомножитель называется основанием степени, а число одинаковых сомножителей называется показателем степени.
Сокращенно степени обозначаются так: а2, а3, а4... и т. д.
Мы сначала будем говорить о простейшем случае возвышения в степень, именно о возвышении в квадрат; а пoсле рассмотрим возвышение и в другие степени.
153. Правило знаков при возвышении в квадрат. Из правила умножения относительных чисел следует, что:
(+2)2=(+2) (+2) = + 4; (+1/3)2=(+1/3)(+1/3) = +1/9;
(—2)2=(—2) (—2) = + 4; (—1/3)2=(—1/3)(—1/3) = +1/9
Вообще:
(+a)2=(+a) (+a) = +a2
(—a)2=(—a) (—a) = +a2
Значит, квадрат всякого относительного числа есть число положительное.