
- •Курсовая работа
- •Структурный анализ механизма
- •Описание механизма
- •1.2. Степень подвижности механизма
- •1.3.Структурные группы механизма
- •3. Кинематический расчет механизма
- •3.1. Определение скоростей методом построения планов скоростей.
- •4. Строим план скоростей для по векторным уравнениям (7) и (8)
- •9. Построим план скоростей для верхнего «мертвого» положения второго поршня в точке с0 ()
- •3.2. Определение ускорений методом построения плана ускорений
- •План ускорений при
- •4. Силовой расчет
- •4.4. Определение векторов сил инерции и главных моментов сил инерции звеньев
- •4.5. Определение реакций в кинематических парах кинетостатическим способом
- •4.5.1. Силовой расчет диады 2-3
- •4.5.2. Силовой расчет диады 4-5
- •4.5.3. Силовой расчет механизма 1ого класса.
- •4.6 Определение уравновешивающей силы с помощью теоремы н.Е. Жуковского о «жестком рычаге»
- •1.1)Проектирование кинематического и силового расчёта многозвенного зубчатого механизма.
- •2.1)Вычерчивание кинематической силы редуктора.
- •2.2)Определение степени подвижности планетарного редуктора.
- •3.1)Определения передаточного числа аналитическим методом.
- •3.2)Определения передаточного числа графическим способом.
- •3,3)Построение угловых скоростей
- •3.4)Нагружение стойки. Определения тормазного (реактивного ) момента.
- •4.1)Определение геометрических параметров пары нормальных колёс.
- •4,2)Расщёт нормального эвольвентного зацепления
- •4,3)Ращёт исправленного зацепления (1-2)
- •Список литературы.
4.4. Определение векторов сил инерции и главных моментов сил инерции звеньев
|
Формулы определения |
Модули |
|
Звено 1 – невесомое вращается вокруг центра О |
|
|
|
|
|
Звено 2 – плоскопараллельное движение; центр масс – s2; |
|
|
|
|
|
Звено 3 – поступательное движение |
|
|
|
|
|
Звено 4 – плоскопараллельное движение; центр масс – s4; |
|
|
|
|
|
Звено 5 – поступательное движение |
|
|
|
|
4.5. Определение реакций в кинематических парах кинетостатическим способом
4.5.1. Силовой расчет диады 2-3
- Изображаем диаду
2-3 в прежнем масштабе длин
![]()
- Сумма моментов относительно точки В
![]()
![]()
отсюда
![]()
![]() 198мм.
198мм.
![]()
- Векторное уравнение сил диады 2-3
![]()
![]()
В этом уравнении
неизвестны величины сил
![]() и
и
![]() .
.
- По этому уравнению строим векторный многоугольник сил.
- Выбираем масштаб
построения.
![]()
Отрезки векторного многоугольника, соответствующие известным силам, будут равны

- Строим векторный многоугольник и находим модули неизвестных сил:
ak=6мм, gk=14мм.
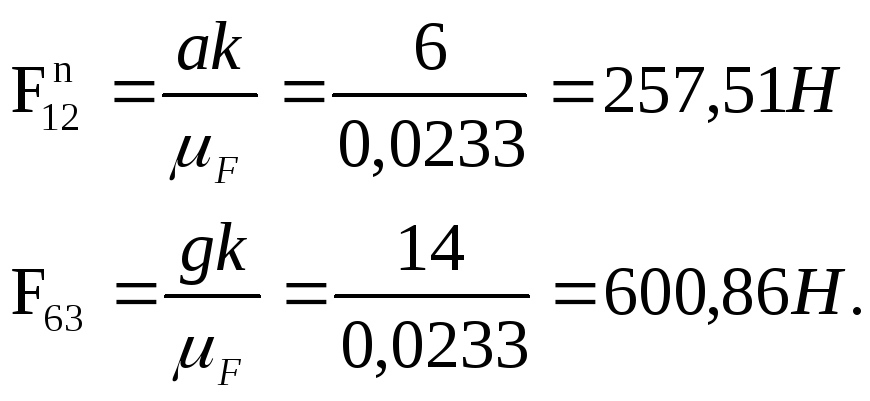
- Находим полную реакцию в шарнире А- в кинематической паре 2.
![]() ,
,
Соединим точку k с точкой с. Замеряем kc=42мм.
![]() .
.
- Найдем реакцию
внутренней кинематической пары ④
![]() в точке В
в точке В
- Реакция в точке В показана в виде двух составляющих
![]()
В точке В имеем реакции
![]() .
.
Составим уравнение суммы всех сил.
![]()
Соединяем точку
e
с точкой k
и направим вектор
![]() в точку k.
в точку k.
Замеряем ek=14мм.
Вычисляем ![]()
Сила
![]() ,
действующая на поршень, равна по величине
,
действующая на поршень, равна по величине
![]() и направлена ей противоположно.
и направлена ей противоположно.
4.5.2. Силовой расчет диады 4-5
Изобразим диаду
4-5 в прежнем масштабе длин
![]()
Уравнение суммы моментов всех сил, действующих на диаду 4-5, относительно точки С.
![]()
![]()
отсюда
![]()
Замеряем
![]() и вычисляем:
и вычисляем:
![]()
Сила получилась отрицательной, следовательно, направление ее не совпадает с направлением, изображенным на рисунке.
- Найдем нормальную
составляющую
![]() и реакцию
и реакцию
![]() со стороны стойки.
со стороны стойки.
Ставим уравнение суммы векторов сил, действующих на диаду.
![]()
![]()
Выбираем масштаб построения векторного многоугольника сил.
Проведем построение
в масштабе
![]() .
.
Отрезки векторного многоугольника, соответствующие известным силам, будут равны:

Построим векторный многоугольник сил и находим модули неизвестных сил:
замеряем ck= 52мм, gk= 48мм;
вычисляем ![]() ;
;
![]() .
.
- Найдем реакцию
внутренней кинематической пары ⑥
![]() в точке С
в точке С
- Реакция в точке С показана в виде двух составляющих
![]()
В точке С имеем реакции
![]() .
.
Составим уравнение суммы всех сил.
![]()
Соединяем точку
e
с точкой k
и направим вектор
![]() в точку k.
в точку k.
Замеряем ek=50мм.
Вычисляем ![]()
Сила
![]() ,
действующая на поршень, равна по величине
,
действующая на поршень, равна по величине
![]() и направлена ей противоположно.
и направлена ей противоположно.
4.5.3. Силовой расчет механизма 1ого класса.
- Изображаем кривошип в том же масштабе длин на
- Записываем два уравнения кинетостатического равновесия
![]()
![]()
- Найдем уравновешивающую силу. Составим уравнение суммы моментов сил относительно точки О.
![]()
отсюда
![]()
замеряем
![]() и вычисляем
и вычисляем
![]()
Находим полную реакцию со стороны стойки, составив векторную сумму сил.
![]()
Неизвестная сила
![]() находится путем построения силового
многоугольника.
находится путем построения силового
многоугольника.
Векторный
многоугольник строим в масштабе
![]() .
.
Отрезки векторного многоугольника, соответствующие известным силам будут равны

Найдем модуль силы
![]() ,
замеряем da=66
мм.
,
замеряем da=66
мм.
вычисляем
![]()

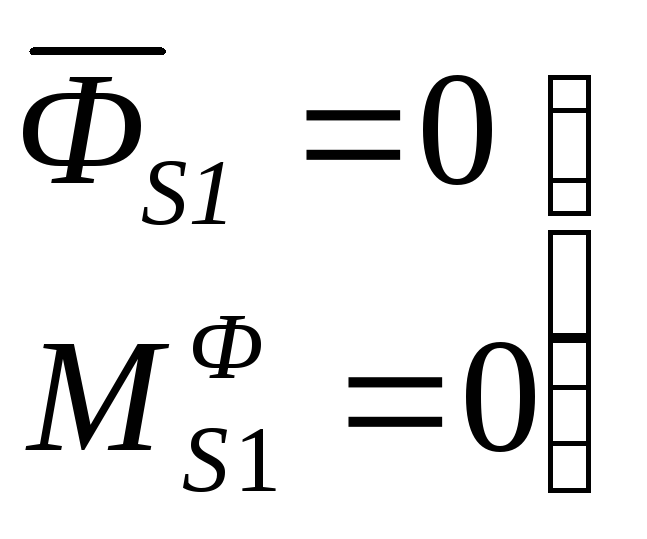 ,
так как
,
так как