12.Змушені коливання, резонанс.

Коливання — фізичний процес, під час якого чергуються інтервали збільшення й зменшення фізичної величини.

Коливаннями або коливальними рухами називають такі види механічного руху чи зміни стану системи, які періодично повторюються в часі, наприклад, механічні коливання тіла на пружині, коливання маятників, коливання струн, вібрації фундаментів будівель, електромагнітні коливання в коливальному контурі. За фізичною природою коливання поділяють на механічні та електромагнітні, за характером коливань - на вільні, вимушені та автоколивання. Коливання, які відбуваються в системі під дією зовнішньої періодичної сили, називаються вимушеними.

Графік ідеалізованого власного коливання являє собою синусоїду або косинусоїду. Однак у будь-якій реальній коливальній системі, внаслідок неминучості дії сил тертя й опору, власні коливання згасають, тобто їх амплітуда зменшується з часом.

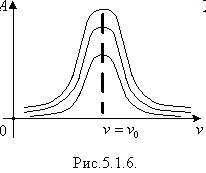
Оскільки в колі відбуваються вимушені коливання, а також можливі власнї коливання, то, очевидно, має місце резонанс: збіг частоти вимушених коливань у колі з частотою власних коливань. Резонансну частоту можна визначити так:

Як бачимо, значення резонансної частоти збігається зі значенням частоти вільних коливань в ідеальному коливальному контурі (формула Томсона).

Якими ж способами можна досягти в колах змінного струму резонансу? Цими способами можуть бути: зміна індуктивності, зміна ємності і зміна частоти струму. Явище резонансу широко використовують в радіотехніці (настроювання контурів), електротехніці (підвищення coscp) тощо.

Резонанс в електричному колі змінного струму спостерігається за умови, що RL = Rc і Z = R

Значення резонансної частоти збігається зі значенням частоти вільних коливань в ідеальному контурі (власних коливань — формула Томсона)

У колі з індуктивністю, ємністю та активним опором у загальному випадку між напругою і силою струму є зсув фаз, який можна визначити за формулами:

Коли в колі досягнуто резонансу (Ri = Rc), зсуву фаз немає: напруга і сила струму мають однакові фази. При цьому й коефіцієнт потужності максимальний: .

Коли у колі змінного струму досягнуто резонансу (RL = RC), то сила струму й напруга мають однакові фази (зсув фаз ф = 0) і коефіцієнт потужності максимальний:

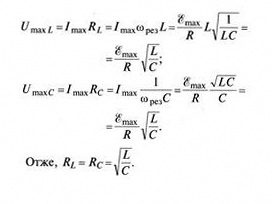
З'ясуємо, якими можуть бути амплітуди напруг на індуктивному та ємнісному опорах за резонансу:

Як бачимо, за резонансу значення цих напруг однакові. А оскільки вони мають протилежні фази, то повністю компенсують одна одну. Ці напруги можуть у багато разів перевищувати напругу, яка подається до кола.

Внаслідок рівності напруг у цьому послідовному колі за резонансу останній резонанс називають резонансом напруг. При резонансі у послідовному колі напруги на індуктивному і ємнісному опорах повністю компенсують одна одну, тому такий резонанс називається резонансом напруг.

13. Резонанс напруги, резонанс струмів.

Резонанс напруг - резонанс, який відбувається в послідовному коливальному контурі при його підключенні до джерела напруги, частота якого збігається з власною частотою контура.

Резонанс напруг можливий у нерозгалуженій ділянці ланцюга, схема якого містить індуктивний L, ємнісний С и резистивный R елементи, тобто в послідовному коливальному контурі. Назва "резонанс напруг" відбиває рівність діючих значень напруг на ємнісному й індуктивному елементах при протилежних фазах, на якій обрана початкова фаза напруги .Якщо при резонансі збільшити в однакове число раз індуктивний і ємнісний опори, то струм у ланцюзі не зміниться, а напруги на індуктивному і ємнісному елементах збільшаться в таке ж число раз. Можна необмежено збільшувати напруги на індуктивному і ємнісному елементах при незмінному струмі джерела. Фізичною причиною цього є коливання значної енергії, що запасається поперемінно в електричному полі ємнісного й у магнітному полі індуктивного елементів.

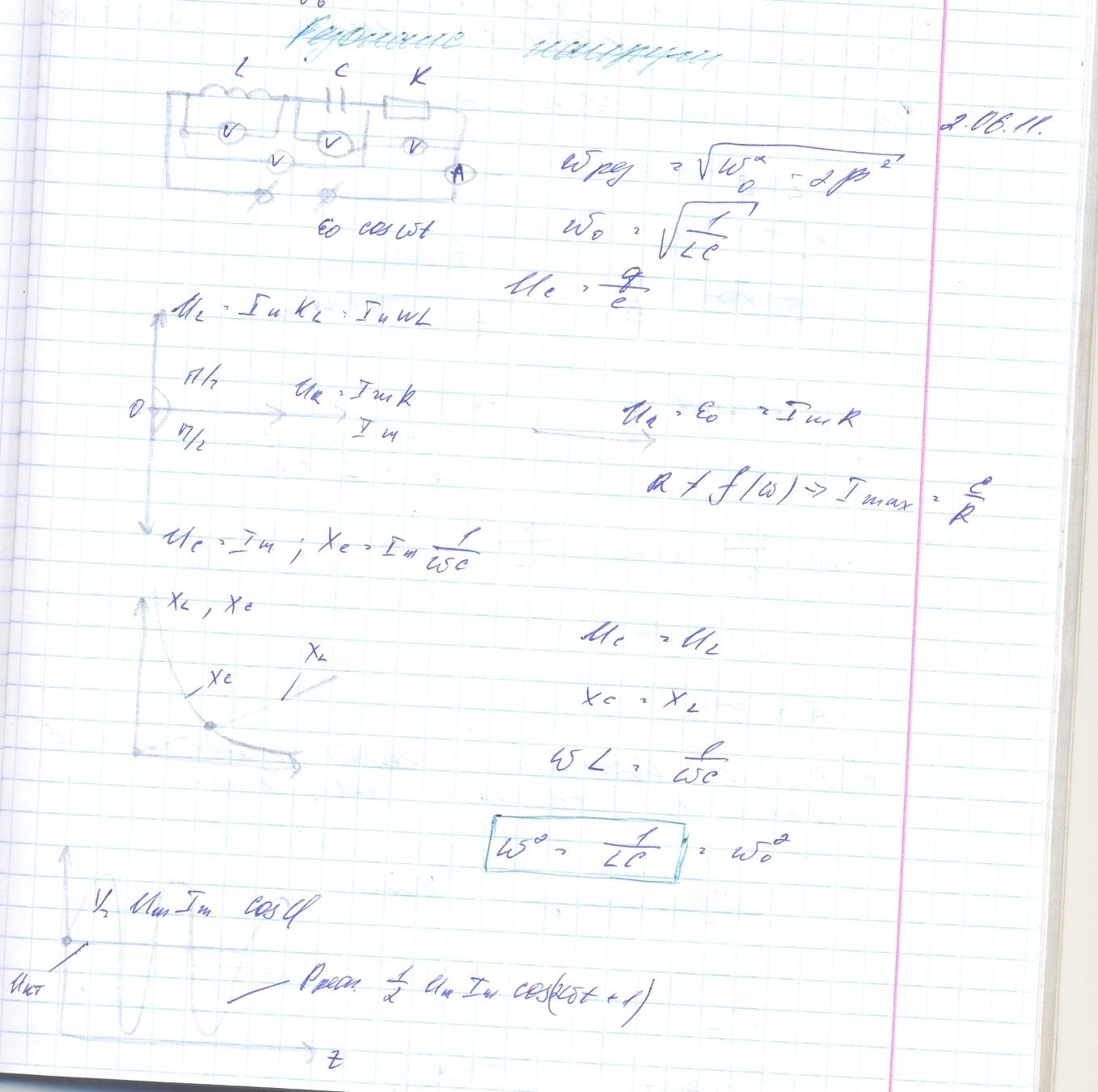
Резонанс струмів –явище резонансу на ділянці електричного кола, що має паралельно злучені індуктивний та емнісний елементи

Резонанс токов

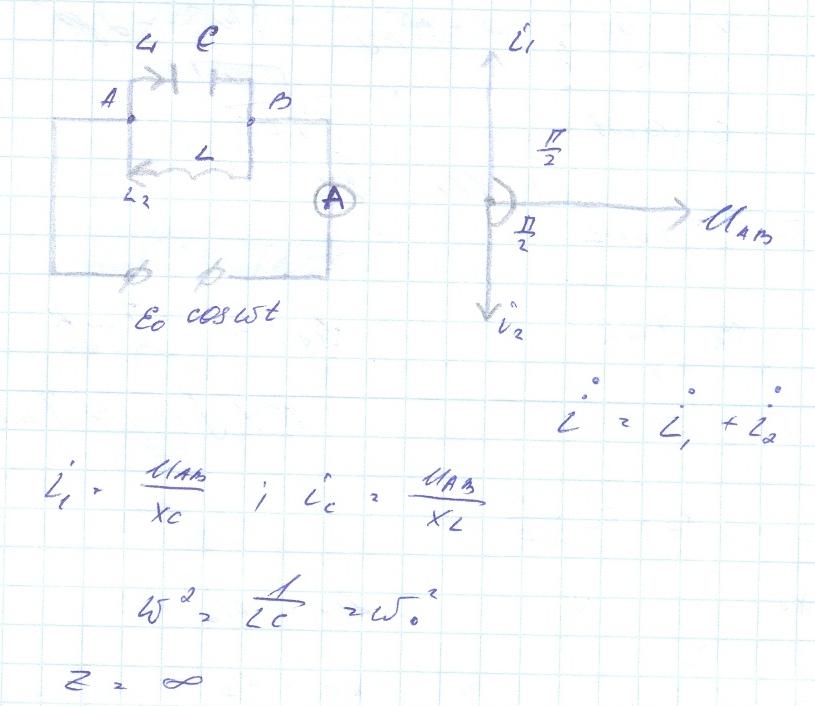
Рассмотрим случай, когда у параллельно соединенных конденсатора и катушки оказались равными их реактивные сопротивления, т. е. XlL = XC.

Если мы, будем считать, что катушка и конденсатор не обладают активным сопротивлением, то при равенстве их реактивных сопротивлений (YL = YC) общий ток в неразветвленной части цепи окажется равным нулю, тогда как в ветвях будут протекать равные токи наибольшей величины. В цепи в этом случае наступает явление резонанса токов.

При резонансе токов, как и при резонансе напряжений, происходит колебание энергии между полем катушки и полем конденсатора. Генератор, сообщив однажды энергию цепи, сказывается как бы изолированным. Его можно было бы совсем отключить, и ток в разветвленной части цепи поддерживался бы без генератора энергией, которую в самом начале запасла цепь. Равно и напряжение на зажимах цепи оставалось бы точно таким, какое развивал генератор.

Значения L, С и f, при которых наступает резонанс токов, определяются, как и при резонансе напряжений (если пренебречь активным сопротивлением контура), из равенства:

ωL = 1 / ωC

Следовательно: fрез = 1 / 2π√LC; Lрез = 1 / ω²С; Срез = 1 / ω²L

Изменяя любую из этих трех величин, можно добиться равенства Xl = Xc, т. е. превратить цепь в колебательный контур.

Резона́нс  — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы .