
- •Правило Саррюса
- •5) Определение
- •9) Описание метода Пусть исходная система выглядит следующим образом
- •Координаты вектора Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
- •13) Операции над векторами
- •Коллинеарные и компланарные векторы
- •6.2. Свойства скалярного произведения
- •6.3. Выражение скалярного произведения через координаты
- •15) Определение
- •Свойства Геометрические свойства векторного произведения
- •Алгебраические свойства векторного произведения
- •17) Правые и левые тройки векторов в трёхмерном пространстве
- •19) Уравнения прямой на плоскости
- •Общее уравнение прямой
- •20) Уравнение прямой, проходящей через две точки
- •21) Уравнение плоскости
- •22) Уравнение плоскости, проходящей через три данные точки
- •24) Числовые последовательности
- •Ограниченные и неограниченные последовательности
- •25) Бесконечно большие и бесконечно малые последовательности
- •Свойства бесконечно малых и бесконечно больших величин и связь между ними
- •29) Второй замечательный предел:
- •32) Определение
- •Определение производной функции через предел
- •34) Производные функции, заданной параметрически
- •35) Определения Для функций
- •36) 1) Физический смысл производной.
6.2. Свойства скалярного произведения
1. Скалярное произведение обладает переместительным свойством: ab=ba
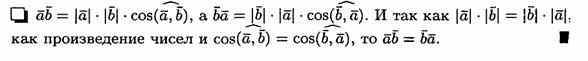

 Решение:
Решение:
![]()
![]()
5. Если векторы а и b(ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а 0b, то а b
.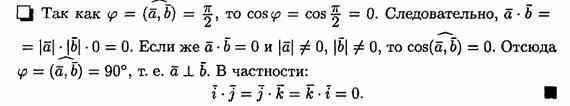
6.3. Выражение скалярного произведения через координаты
Пусть заданы два вектора
![]()
Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:
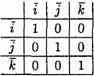
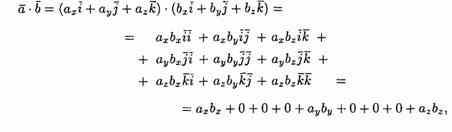
т.е
![]()
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.
15) Определение
Векторным
произведением
вектора
![]() на
вектор
на
вектор
![]() в
пространстве
в
пространстве
![]() называется
вектор
называется
вектор
![]() ,
удовлетворяющий следующим требованиям:
,
удовлетворяющий следующим требованиям:
-
длина вектора
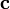 равна
произведению длин векторов
равна
произведению длин векторов
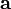 и
и
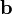 на
синус
угла
на
синус
угла
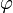 ;
между ними
;
между ними
![]()
-
вектор
 ортогонален
каждому из векторов
ортогонален
каждому из векторов
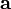 и
и
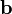
-
вектор
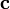 направлен
так, что тройка векторов
направлен
так, что тройка векторов
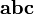 является
правой.
является
правой. -
в случае пространства
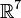 требуется
ассоциативность тройки векторов
требуется
ассоциативность тройки векторов
 .
.
Обозначение:
![]()
В литературе[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.
Свойства Геометрические свойства векторного произведения
-
Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
-
Модуль векторного произведения
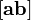 равняется
площади S
параллелограмма,
построенного на приведённых к общему
началу векторах
равняется
площади S
параллелограмма,
построенного на приведённых к общему
началу векторах
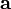 и
и
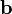 (см.
Рисунок 1)
(см.
Рисунок 1) -
Если
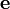 —
единичный
вектор, ортогональный векторам
—
единичный
вектор, ортогональный векторам
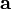 и
и
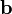 и
выбранный так, что тройка
и
выбранный так, что тройка
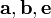 —
правая, а S —
площадь параллелограмма, построенного
на них (приведённых к общему началу),
то для векторного произведения
справедлива формула:
—
правая, а S —
площадь параллелограмма, построенного
на них (приведённых к общему началу),
то для векторного произведения
справедлива формула:
![]()
-
Если
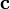 —
какой-нибудь вектор, π —
любая плоскость, содержащая этот вектор,
—
какой-нибудь вектор, π —
любая плоскость, содержащая этот вектор,
 —
единичный вектор, лежащий в плоскости
π
и ортогональный к
—
единичный вектор, лежащий в плоскости
π
и ортогональный к
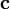 ,
,
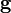 —
единичный вектор, ортогональный к
плоскости π
и направленный так, что тройка векторов
—
единичный вектор, ортогональный к
плоскости π
и направленный так, что тройка векторов
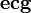 является
правой, то для любого лежащего в плоскости
π
вектора
является
правой, то для любого лежащего в плоскости
π
вектора
 справедлива
формула
справедлива
формула
![]()
-
При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.
![]()
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
![]()
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0, если векторы параллельны.
