2.Алгоритм поиска минимума интегральной оценки в пространстве параметров.

Уменьшение оценки будем осуществлять подбором параметров tau И teta корректирующего элемента. Исходя из их допустимых значений, которые определяются рис.12.5, построим начальный симплекс с вершинами в точках с координатами, задаваемыми

№точки	tau	teta	Интегр.оценка
1	0.230	0.350	3.7203
2	0.220	1.150	1.6862
3	0.086	0.710	0.1664

Из таблицы видно, что наибольшее значение интегральной оценки соответствует параметрам первой точки. Из этой точки делается пробный шаг в новую точку с координатами, вычисляемыми по формулам

В результате подсчета получаем новое значение интегральной оценки (Табл.13.2)

№ точки			Интегр.оценка
2	0.220	1.150	1.6862
3	0.086	0.710	0.1664
4	0.076	1.510	0.6629

Пробный шаг привел к уменьшению интегральной оценки и поэтому принимается. Нетрудно видеть, что геометрически этот шаг соответствует построению отрезка, проведенного из вершины с наибольшей интегральной оценкой через середину противоположной стороны треугольника-симплекса, образованного тремя первоначально выбранными точками. Во вновь образованной таблице «конкурирующими» вершинами оказались две прежних и одна новая. Однако повторение операции с пробным шагом не приведет к положительному результату, ибо новая вершина окажется вне пределов зоны устойчивости (рис.12.5). В этом случае необходимо сократить вдвое длину ребер симплекса, причем вершина с наименьшей интегральной оценкой остается неподвижной. В данном случае такой вершиной служит третья точка. Формулы для вычисления координат двух новых вершин очевидны:

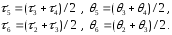
После подсчета интегральных оценок получаем

№ точки			Интегр.оценка
3	0.086	0.710	0.16640
5	0.081	1.110	0.21388
6	0.153	0.930	0.39266

Последующие шаги приводят к постепенному уменьшению интегральной оценки переходного процесса. Остановка всей вычислительной процедуры производится по признаку малого выигрыша в интегральной оценке, которая по принятой терминологии в теории наименьших квадратов является функцией риска. В приведенном примере достаточно малой интегральной оценкой можно считать величину I₂ = 0.046608.

БИЛЕТ № 12

1.Определение устойчивости движения по а.М. Ляпунову.

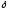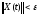Движение X(t)=0 называется устойчивым, если для любых >0 и T>0 существует такое, что из условия следует для любого t >T.

Это определение допускает наглядную геометрическую интерпретацию (рис.7.1).Границы множеств векторов с постоянной нормой изображаются здесь окружностями, а одна из осей используется для отсчета времени. В случае устойчивости решение, начинающееся внутри некоторой окружности с течением времени попадает внутрь цилиндра сколь угодно малого радиуса и в дальнейшем не покидает его.

Рис.7.1. Геометрическая интерпретация устойчивого решения