1.Типовые тестовые воздействия и их краткая характеристика.

1.Единичная ступенчатая функция

2.Дельта-функция (функция Дирака) причем ,

3.Гармоническое входное воздействие, представляющее собой , либо , либо их линейную комбинацию.

2.Импульсная переходная характеристика линейной системы управления.

Среди тестовых сигналов особая роль принадлежит функции или функции Дирака, о которой упоминалось в лекции 1. Реакция динамической системы на это входное воздействие называется импульсной переходной характеристикой, которую обычно обозначают символом . Пользуясь этим понятием, можно получить выражение для вычисления реакции системы на воздействие произвольного типа, в том числе и на воздействие типа непрерывной функции времени.

Формально импульсную переходную характеристику можно определить как оригинал по отношению к передаточной функции. В самом деле, т.к. изображение единичного импульса равно 1, то изображение можно записать как .

Если импульс возникает в момент , то реакция на него будет также сдвинута и равна , причем поскольку эффект не может предшествовать причине, вызвавшей его , то при .

С другой стороны любая ограниченная функция может быть представлена суммой элементарных импульсов , где и при остальных значениях аргумента. В силу линейности реакция системы на сумму импульсов будет равна сумме реакций на каждое слагаемое, т.е. .

Переходя к пределу при , получаем формулу, известную как интеграл Дюамеля . (10.1)

Если иметь в виду замечание о причине, вызывающей импульсную реакцию, то в формуле (10.1) верхний предел можно ограничить текущим моментом времени, т.е. . (10.2)

В случае, когда входной сигнал равен нулю при отрицательных значениях аргумента в формулах (10.1) и (10.2) нижний предел интеграла также равен нулю.

БИЛЕТ № 3

1.Периодические и непериодические сигналы. Преобразование Лапласа.

Функция f(t) называется периодической, если существует величина T, такая что для любого значения t f(t+T)=f(t). Наименьшая из величин T называется периодом.

Весьма широкий класс периодических функций можно разложить в ряд Фурье .(2.1)

Здесь коэффициенты a_k и b_k вычисляются с помощью соотношений ,(2.2)

Ряду Фурье можно придать комплексную форму, если воспользоваться соотношениями и

.

Введем обозначение и, замечая, что согласно (2.2) , запишем ряд (2.1) в комплексной форме(2.3)

Нетрудно заметить, что коэффициенты в (2.3) вычисляются с помощью формулы, вытекающей из (2.2), а именно . (2.4)

Введем обозначение . Очевидно при этом приращение и, следовательно, согласно (2.3) и (2.4), (2.5)

Переходя к пределу в (2.5) при 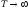и обозначая , (2.6) запишем (2.7)

Мы получили соотношения, которые играют в дальнейшем важную роль во всей изучаемой нами дисциплине. Это прямое (2.6) и обратное (2.7) преобразования Фурье. Предельный переход означает, что мы распространили ряд Фурье на непериодические функции, и этим существенно расширили класс исследуемых сигналов.

Заметим, что функция , фигурирующая в формуле прямого преобразования должна допускать сходимость несобственного интеграла. Разумеется, не все функции обладают этим свойством. Например, функция 1/t не может быть преобразована по Фурье - она недостаточно быстро убывает (кроме того, она имеет разрыв при t=0). Для того, чтобы гарантировать сходимость несобственного интеграла в (2.5),во многих случаях достаточно предварительно умножить преобразуемую функцию на экспоненту с отрицательным показателем, т.е. рассматривать в дальнейшем такие функции, которые допускают существование интеграла (2.8)

Константа с называется абсциссой абсолютной сходимости, а преобразование вида (2.8) называется прямым преобразованием Лапласа.

В соответствии с введенным обозначением для параметра s можно записать и обратное преобразование (2.7) в форме .(2.9)

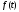принято называть изображением по Лапласу функции , которая в свою очередь называется оригиналом.