Основное уравнение мкт

, где k является постоянной Больцмана (отношение универсальной газовой постоянной R к числу Авогадро N_A), i — число степеней свободы молекул (i = 3 в большинстве задач про идеальные газы, где молекулы предполагаются сферами малого радиуса, физическим аналогом которых могут служить инертные газы), а T - абсолютная температура.

Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).

[Править]Вывод основного уравнения мкт

Пусть имеется кубический сосуд с ребром длиной l и одна частица массой m в нём.

Обозначим скорость движения v_x, тогда перед столкновением со стенкой сосуда импульс частицы равен mv_x, а после — − mv_x, поэтому стенке передается импульс p = 2mv_x. Время, через которое частица сталкивается с одной и той же стенкой, равно .

Отсюда следует:

Так как давление , следовательно сила F = p * S

Подставив, получим: 

Преобразовав: 

Так как рассматривается кубический сосуд, то V = Sl

Отсюда:

.

Соответственно,  и .

Таким образом, для большого числа частиц верно следующее: , аналогично для осей y и z.

Поскольку , то . Это следует из того, что все направления движения молекул в хаотичной среде равновероятны.

Отсюда 

или .

Пусть  — среднее значение кинетической энергии всех молекул, тогда:

, откуда .

Для одного моля выражение примет вид 

[Править]Уравнение среднеквадратичной скорости молекулы

Уравнение среднеквадратичной скорости молекулы легко выводится из основного уравнения МКТ для одного моля газа.

, для 1 моля N = N_a, где N_a — постоянная Авогадро

N_am = M_r, где M_r — молярная масса газа

Отсюда окончательно

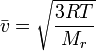
32. вантовая теория теплоёмкостей Эйнштейна − была создана Эйнштейном в 1907 году, при попытке объяснить экспериментально наблюдаемую зависимость теплоёмкости от температуры.

При разработке теории Эйнштейн опирался на следующие предположения:

• Атомы в кристаллической решетке ведут себя как гармонические осцилляторы, не взаимодействующие друг с другом.

• Частота колебаний всех осцилляторов одинакова.

• Число осцилляторов в 1 моле вещества равно 3N_a, где N_a - число Авогадро.

• Энергия их квантована:  , 

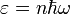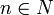
• Число осцилляторов с различной энергией определяется распределением Больцмана: 

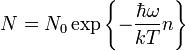
Внутренняя энергия 1 моля вещества:

.

 находится из соотношения для среднего значения:

и составляет:

,

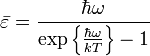отсюда:

.

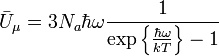Определяя теплоёмкость как производную внутренней энергии по температуре, получаем окончательную формулу для теплоёмкости:

.

31. Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.

Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высокихтемпературах, в других условиях её соответствие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут.

Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергияU становится функцией не только температуры, но и объёма.

Уравнение состояния

Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь междудавлением, объёмом и температурой.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

где

• p — давление,

• V — молярный объём,

• T — абсолютная температура,

• R — универсальная газовая постоянная.

Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка a учитывает силы притяжения между молекулами (давление на стенку уменьшается, т.к. есть силы, втягивающие молекулы приграничного слоя внутрь), поправка b — силы отталкивания (из общего объёма вычитаем объём, занимаемый молекулами).

Для ν молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

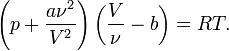
где

• V — объём,

30. Закон Пуассона является законом распределения вероятностей, например, для следующих случайных величин.

а) Пусть на интервале ]0, N[ оси Ох случайно размещаются п точек независимо друг от друга, причем события, заключающиеся в попадании одной точки на любой наперед заданный отрезок постоянной (например, единичной) Длины, равновероятны.

Если ЙЙЙ , то случайная величина X, рав­ная числу точек, попадающих на заданный отрезок единичной длины (которая может принимать значения О, 1, …, т, …)» распределяется по закону Пуассона.

б) Если п равно среднему числу вызовов абонентов, поступающих за один час на данную телефонную станцию, то число вызовов, поступающих за одну минуту, приближенно распределяется по закону Пуассона, причем а = /г/60.

Математическое ожидание и дисперсия случайных величин, распределенных по биномиальному закону и закону Пуассона, определяются по следующим формулам:

для биномиального закона: М(Х) = пр; D(X) = npq;

для закона Пуассона: М(Х) = а; D(X) = a.

29. Закон Бо́йля — Марио́тта — один из основных газовых законов, открытый в 1662 году Робертом Бойлем и независимо переоткрытый Эдмом Мариоттом в 1676 году. Закон является частным случаемуравнения состояния идеального газа.

Закон Бойля — Мариотта гласит:

При постоянной температуре и массе идеального газа произведение его давления иобъёма постоянно.

В математической форме это утверждение записывается следующим образом

pV = const,

где p — давление газа; V — объём газа.

28. Уравнение состояния идеального газа. (Уравнение Менделеева—Клапейрона.) Изопроцессы.      Состояние данной массы газа полностью определено, если известны его давление, температура и объем. Эти величины называют параметрами состояния газа. Уравнение, связывающее параметры состояния, называют уравнением состояния.           Для произвольной массы газа состояние газа описывается уравнением Менделеева—Клапейрона: pV = mRT/M, где р — давление, V — объем, m — масса, М — молярная масса, R — универсальная газовая постоянная. Физический смысл универсальной газовой постоянной в том, что она показывает, какую работу совершает один моль идеального газа при изобарном расширении при нагревании на 1 К (R = 8,31 ДжДмоль • К)).           Уравнение Менделеева—Клапейрона показывает, что возможно одновременное изменение трех параметров, характеризующих состояние идеального газа. Однако многие процессы в газах, происходящие в природе и осуществляемые в технике, можно рассматривать приближенно как процессы, в которых изменяются лишь два параметра. Особую роль в физике и технике играют три процесса: изотермический, изохорный и изобарный.           Изопроцессом называют процесс, происходящий с данной массой газа при одном постоянном параметре — температуре, давлении или объеме. Из уравнения состояния как частные случаи получаются законы для изопроцессов.           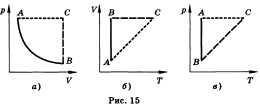Изотермическим называют процесс, протекающий при постоянной температуре. Т = const. Он описывается законом Бойля—Мариотта: pV = const.           Изохорным называют процесс, протекающий при постоянном объеме. Для него справедлив закон Шарля: V = const, p/T = const.           Изобарным называют процесс, протекающий при постоянном давлении. Уравнение этого процесса имеет вид V/T = const прир = const и называется законом Гей-Люссака. Все процессы можно изобразить графически (рис. 15).           Реальные газы удовлетворяют уравнению состояния идеального газа при не слишком высоких давлениях (пока собственный объем молекул пренебрежительно мал по сравнению с объемом сосуда,