Каноническое уравнение прямой.

(Термин «каноническое» - от греч. – правило, предписание, образец. Понимается как «типовой», «традиционный»).

Определение. Любой ненулевой вектор, параллельный данной прямой, называется направляющим вектором этой прямой.

Найдем уравнение прямой L, проходящей через заданную точку плоскости М₀(х₀;у₀) параллельно заданному вектору q={l,m}.

Рассмотрим произвольную точку М(х,у).

Точка М(х;у)L , когда векторы ММ₀=(х-х₀)i+(y-y₀)j и вектор q=li+mj коллинеарны, т.е.  когда координаты векторов пропорциональны, т.е.

(5) – каноническое уравнение прямой.

Замечание. В уравнении (5) одно из чисел l или m может оказаться равным нулю (оба числа l и m равняться нулю не могут, т.к. вектор q={l,m} ненулевой). Всякую пропорцию понимаем как равенство ad=cb. Тогда обращение в нуль одного из знаменателей в (5) означает обращение в нуль и соответствующего числителя. Так, например, если l=0, то m0 и из равенства l(y-y₀)=m(x-x₀) х-х₀=0, т.е. х=х₁ – уравнение прямой, параллельной оси Ох.)

Параметрическое уравнение прямой.

В каноническом уравнении (5) обозначим равные, но переменные для различных положений точки М, отношения через параметр t. Т.к. один из знаменателей (7) отличен от нуля, а соответствующий числитель может принимать любые значения, то областью изменения параметра t является вся вещественная ось, т.е. tR:

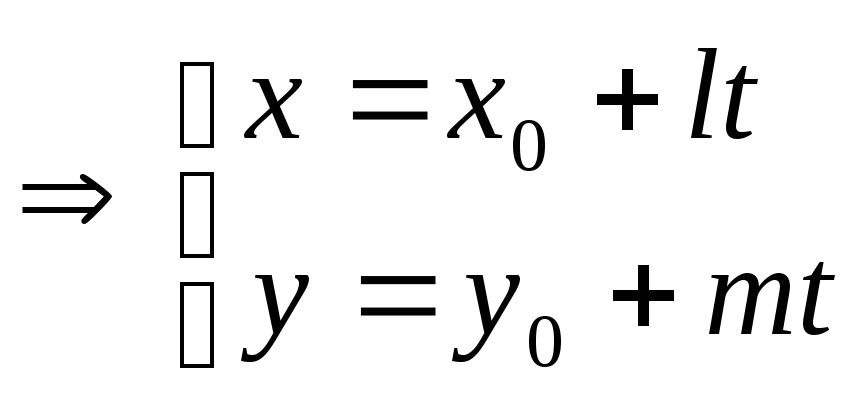tR (6) – параметрическое уравнение прямой.

Уравнение прямой, проходящей через 2 заданные точки.

Т.к. точка М₁L, то каноническое уравнение этой прямой имеет вид: ,

Где параметры l и m являются координатами направляющего вектора q, в качестве которого можно выбрать вектор М₁М₂. Тогда

q=li+mj=М₁М₂=(х₂-х₁)i+(y₂-y₁)j. В итоге получаем:

(7) – уравнение прямой, проходящей через 2 заданные точки.

Пример. Уравнение прямой, проходящей через точки А(3;-5), В(-2;1):

Замечание. Если в (7) один из знаменателей равен нулю, считают, что соответствующий числитель так же равен нулю.

Возможны случаи:

1. х₂-х₁=0, тогда х₁=х₂=const=a, x-x₁=0 x=a – уравнение вертикальной прямой.

2. y₂-y₁=0, тогда y₁=y₂=const=b, y-y₁=0 y=b – уравнение горизонтальной прямой.

Уравнение прямой в отрезках.

Пусть прямая L проходит через точки А(а;0) и В(0;b) (т.е. отсекает от осей координат отрезки длиной а и b). Уравнение этой прямой имеет вид:

или, после преобразования,

(8) – уравнение прямой в отрезках.

Это уравнение можно получить и из полного уравнения Ах+Ву+С=0, переписав его в виде (т.к. в полном уравнении коэффициенты А,В и С не равны нулю):

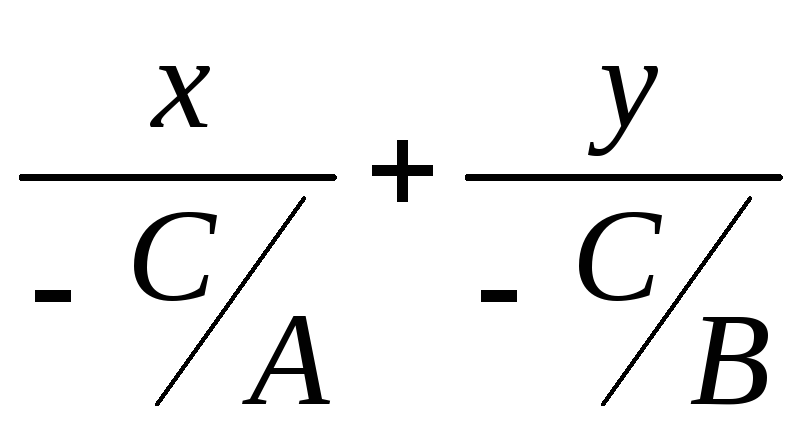=1 и положить а=-, b=-.

Уравнение прямой с угловым коэффициентом.

Рассмотрим произвольную прямую L, не параллельную оси Ох. Определим угол наклона прямой L к оси Ох. Допустим прямая L пересекает ось Ох в точке С. Возьмем на оси Ох произвольную точку А, лежащую по ту сторону от точки С, куда направлена ось Ох, а на прямой L произвольную точку М, лежащую по ту сторону от точки С, куда направлена ось Оу. Угол =МСА- угол наклона прямой L к оси Ох.

Если прямая параллельна оси Ох или совпадает с ней, то угол наклона этой прямой к оси Ох считается равным нулю.

Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой k=tg α. Если прямая параллельна оси Ох или совпадает с ней, то k=0. а для прямой, перпендикулярной оси Ох угловой коэффициент не существует.

Выведем уравнение прямой, проходящей через данную точку М₀(х₀;у₀) и имеющую данный угловой коэффициент k.

Теорема. Если прямая не перпендикулярна оси Ох и имеет направляющий вектор q={l,m}, то угловой коэффициент этой прямой k=.

Доказательство. Пусть  - угол наклона прямой к оси Ох, а  - угол наклона вектора q={l,m} к оси Ох. Возможны 4 случая.

В случаях 1) и 3) = и для проекций вектора q на оси Ох и Оу справедливы формулы:

l=qcos , m=qcos=qsin .

В случаях 2) и 4) =- и для проекций вектора q на оси Ох и Оу справедливы формулы:

l=qcos , m=-qsin .

Т.о. в случаях 1) и 3) tg=tg и =tg, а в случаях 2) и 4) tg=-tg и =-tg,

Следовательно, во всех 4-х случаях tg= tg. Ч.т.д.

Рассмотрим каноническое уравнение . Умножим обе части уравнения на m, учитывая, что k=, получим:

у-у₀=k(х-х₀) (9)

Обозначим через b постоянную b=у₀-kх₀ и уравнение (9) примет вид:

y=kx+b (10) – уравнение прямой с угловым коэффициентом.

Здесь b – величина отрезка, отсекаемого данной прямой на оси Оу, начиная от начала координат (т.е. координата точки пересечения прямой с осью Оу.)

k=.

Если известны координаты 2-х точек, лежащих на прямой, то ее угловой коэффициент равен: k=.

Уравнение (10) не является общим, т.е. не описывает всевозможные случаи расположения прямой на плоскости. Так, например, если α=, то k=tgα не существует. (Переход от уравнения (2) к (3): Ах+Ву+С=0 )

Пример. Найти угол наклона прямой 5х-3у+2=0 к оси Ох.

у=, k=tgα=5/3, α=arctg 5/3.

Рассмотрим частные случаи:

1. При b=0 получаем y=kx – уравнение прямой, проходящей через начало координат. При k=1(1= tg Π/4) получаем уравнение у=х биссектрисы I и III координатных углов, при k=-1 (-1=tg 3Π/4) – уравнение – у=-х – биссектрисы II и IV координатных углов.

2. k=tgα=0, т.е. α=0. Получаем у=b – уравнение прямой, параллельной оси Ох. При b=0 – уравнение самой оси Ох: у=0.

3. При α= прямая перпендикулярная оси Ох и k=tg не существует. Т.о. у вертикальной прямой нет углового коэффициента. Пусть эта прямая отсекает оси Ох отрезок, равный а. Тогда уравнение вертикальной прямой - х=а, а уравнение оси Оу: х=0.