Взаимное расположение прямых на плоскости.

Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых.

1) Прямые заданы общими уравнениями.

L₁: А₁х+В₁у+С₁=0

L₂: А₂х+В₂у+С₂=0

Их нормальные векторы, соответственно, n₁=A₁i+B₁j и n₂=A₂i+B₂j

Угол между прямыми L₁ и L₂ можно определить как угол между векторами n₁ и n₂:

cos φ=, т.е. cos φ= (10)

В этом случае, если l1||l2,то и n1||n2. По условию коллинеарности векторов:

Для того, чтобы прямые L₁ и L₂ совпадали .

Если , то прямые L₁ и L₂ пересекаются в одной точке.

Если L₁L₂, то n₁n₂. По условию ортогональности векторов: n₁·n₂=0, т.е.

А₁А₂+В₁В₂=0.

2) Прямые заданы каноническими уравнениями.

L₁: ; L₂:

Их направляющие векторы, соответственно, q₁={l₁;m₁} и q₂={l₂;m₂}.

Угол между прямыми L₁ и L₂ можно определить как угол между векторами q₁ и q₂:

cos φ=, т.е. cos φ= (11)

В этом случае, если l1||l2,то и q1||q2. По условию коллинеарности векторов:

Если , то прямые L₁ и L₂ пересекаются в одной точке.

Если L₁L₂, то q₁q₂. По условию ортогональности векторов: q₂·q₂=0, т.е.

l₁l₂+m₁m₂=0.

3) Прямые заданы уравнениями с угловыми коэффициентами.

Пусть даны две прямые L₁ и L₂:

y=k₁x+b₁ y=k₂x+b₂

k₁=tg α₁ k₂=tg α₂

Угол между прямыми (L₁ˆL₂)=φ . Тогда

α₁+φ= α₂ → φ=α₂-α₁

tgφ=tg(α₂-α₁)= tgφ= (12)

Если в этой формуле поменять местами k₁ и k₂, то эта формула определит другой угол между прямыми, смежный по отношению к предыдущему (тангенсы этих углов отличаются только знаком).

Если L₁||L₂, то tgφ=0, следовательно k₂-k₁=0, т.е. k₂=k₁ – у параллельных прямых одинаковые угловые коэффициенты.

Если L₁L₂, то φ=Π/2, значит 1+k₁k₂=0, т.е. для угловых коэффициентов перпендикулярных прямых верно соотношение: k₁k₂=-1 или k₁=-1/k₂.

Нормированное (нормальное) уравнение прямой.

Рассмотрим произвольную прямую L. Проведем через начало координат О прямую nL, Р=Ln – точка пересечения прямых. n –единичный вектор прямой n, и, следовательно, нормальный вектор прямой L, его направление совпадает с направлением отрезка ОР (если точки О и Р совпадают, то направление вектора n выбирают произвольно).

Выразим уравнение прямой L через два параметра: длину р отрезка ОР и угол  между вектором n и осью Ох.

Т.к. n – единичный вектор, то его координаты равны проекциям на оси координат:

n={cos ,sin } (13)

Точка М(х,у) лежит на прямой L тогда и только тогда, когда проекция вектора на ось, определяемую вектором n, равна р, т.е. при условии пр_n=р (14)

Т.к. , то nпр_n=пр_n=n (15)

n=х cos +уsin  (16)

Т.о. точка М(х,у) лежит на прямой L тогда и только тогда, когда координаты этой точки удовлетворяют уравнению:

х cos +уsin =р или х cos +уsin -р=0 (17)– нормированное (нормальное) уравнение прямой.

Общее уравнение прямой Ах+Ву+С=0 можно преобразовать в нормальное.

Если прямая задана общим уравнением Ах+Ву+С=0 и нормированным уравнением х cos +уsin -р=0, то найдется число t такое, что:

tА=cos, tB=sin, tC=-p.

Возведя в квадрат первые два равенства и сложив их, получим: t²(A²+B²)=1.

Тогда t=.

Т.к. всегда расстояние р0, то из равенства tC=-p заключаем, что знак t противоположен знаку C.

Т.о., для приведения общего уравнения прямой Ах+Ву+С=0 к нормированному виду, следует умножить его на нормирующий множитель t=, знак которого противоположен знаку С.

Если С=0, то прямая проходит через начало координат (р=0). В этом случае знак нормирующего множителя можно выбирать любым.

Пример. Написать нормированное уравнение прямой 3х-4у+10=0.

Т.к. С=10>0. то нормирующий множитель равен . Нормированное уравнение имеет вид: -х+у-2=0. Здесь р=2, cos =-, sin =, =.

Отклонение точки от прямой.

Даны прямая L:Ах+Ву+С=0 и точка М₀(х₀;у₀), не лежащая на ней. Расстоянием от точки М₀ до прямой L называется длина перпендикуляра М₀М₁, опущенного из этой точки на прямую: d=ρ(M₀,L).

Определение. Отклонением  точки М₀(х₀;у₀) от прямой L называется число + d в случае, когда точка М₀ и начало координат О лежат по разные стороны от прямой L, и число –d, когда точки М₀ и О лежат по одну сторону от прямой L.

Если начало координат О лежит на прямой L, то полагают отклонение равным +d в том случае, когда точка М₀ по ту сторону от L, куда направлен нормальный вектор n, и равным -d в противном случае.

Теорема. (с. 128) Пусть прямая L задана нормированным уравнением

х cos +уsin -р=0 (17). Тогда отклонение точки М₀(х₀,у₀) от прямой L, равно:

=х₀ cos +у₀ sin -р (18)

Учитывая процедуру преобразования общего уравнения прямой в нормальное, получаем формулу для расстояния от точки М₀(х₀;у₀) до прямой L, заданной своим общим уравнением: d= (19)

Формула (19) позволяет найти и расстояние от точки до прямой.

Пример. Найти длину высоты ВН ΔАВС, если В(1;2), а уравнение прямой, содержащей сторону АС: 6х-8у+5=0.

Находим длину ВН как расстояние от точки В до прямой АС: =0,5.

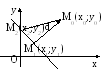
Рассмотрим точку М₂L, ее координаты удовлетворяют уравнению прямой, т.е. Ах₂+Ву₂+С=0 (*). Координаты вектора =(х₀-х₂;у₀-у₂).

Вектор n=(A;B) - нормальный вектор прямой (в его качестве можно рассмотреть вектор , т.к. L). Тогда

d=

(т.к. из (*) С=- Ах₂-Ву₂)