
- •Уравнение линии на плоскости.
- •Параметрическое уравнение линии.
- •2. Полярная система координат (пск).
- •Связь между декартовыми и полярными координатами точки.
- •Классификация плоских линий.
- •Уравнение поверхности в пространстве.
- •Классификация поверхностей.
- •4. Прямая на плоскости.
- •Неполные уравнения прямой. (Частные случаи).
- •Каноническое уравнение прямой.
- •Параметрическое уравнение прямой.
- •Уравнение прямой, проходящей через 2 заданные точки.
- •Уравнение прямой в отрезках.
- •Уравнение прямой с угловым коэффициентом.
- •Взаимное расположение прямых на плоскости.
- •1) Прямые заданы общими уравнениями.
- •В этом случае, если l1||l2,то и n1||n2. По условию коллинеарности векторов:
- •2) Прямые заданы каноническими уравнениями.
- •В этом случае, если l1||l2,то и q1||q2. По условию коллинеарности векторов:
- •3) Прямые заданы уравнениями с угловыми коэффициентами.
- •Нормированное (нормальное) уравнение прямой.
- •Уравнение пучка прямых.
- •Расстояние от точки до прямой. Кривые II –го порядка.
- •Аналитическая геометрия в пространстве (r3)
Аналитическая геометрия в пространстве (r3)
Д ля
описания точек, векторов, линий,
поверхностей в пространстве будем
использовать декартову систему координат
(ДСК) Т.е. установим взаимно однозначное
соответствие между тройкой чисел (х;y;z)
и точкой пространства М. Набор чисел
(х;y;z) называется координатами точки М.
ля
описания точек, векторов, линий,
поверхностей в пространстве будем
использовать декартову систему координат
(ДСК) Т.е. установим взаимно однозначное
соответствие между тройкой чисел (х;y;z)
и точкой пространства М. Набор чисел
(х;y;z) называется координатами точки М.
Поверхностью в пространстве называется множество точек {M(x;y;z)}, координаты которых удовлетворяют заданному уравнению:
z=f(x;y) (1) – явное уравнение линии в ДСК
F(x;y;z)=0 (2) - неявное уравнение линии в ДСК
(Уравнение (1) может быть получено из уравнения (2) путем выражения из этого уравнения одной переменной через другие.
Е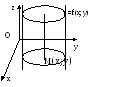 сли
уравнение (2) не содержит какой-либо
координаты х,у или z, то получаем уравнение
цилиндрической поверхности, которая
параллельна оси, соответствующей
отсутствующей переменной. F(x;y)=0
сли
уравнение (2) не содержит какой-либо
координаты х,у или z, то получаем уравнение
цилиндрической поверхности, которая
параллельна оси, соответствующей
отсутствующей переменной. F(x;y)=0
x2+y2=R2
Линия в пространстве R3 определяется как линия пересечения двух поверхностей.
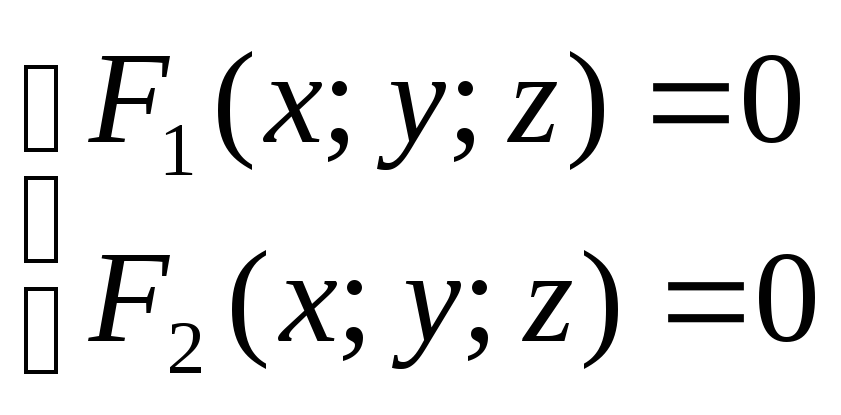 (3)
– общее уравнение линии в пространстве.
(3)
– общее уравнение линии в пространстве.
Линию в пространстве можно так же задать параметрически:
 (4)
(4)
Сфера.
Сферой в пространстве называется множество точек равноудаленных от заданной точки М0(х0;у0;z0) – центра сферы.
Пусть М(х;у;z) – некоторая переменная точка сфера. Расстояние от точки М до центра М0 постоянно и равно радиусу сферы, т.е. d(M0M)=const=R
R=![]()
R2=(x-x0)2+(y-y0)2+(z-z0)2 – уравнение сферы.
1. Сборник задач по математике для втузов, Т.1. Под ред. А.В. Ефимова, А.С. Поспелова.
2. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа. Под ред. А.В. Ефимова, Б.П. Демидовича.
