28

Уравнение линии на плоскости.

Пусть на плоскости  задана декартова прямоугольная система координат Оху и некоторая линия L.

Определение. Уравнение F(x;y)=0 (1) называется уравнением линии L (относительно заданной системы координат), если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии L, и не удовлетворяют координаты х и у ни одной точки, не лежащей на линии L.

Т.о. линией на плоскости называется геометрическое место точек {M(x;y)}, координаты которых удовлетворяют уравнению (1).

Уравнение (1) определяет линию L.

Пример. Уравнение окружности.

Окружность – множество точек, равноудаленных от заданной точки М₀(х₀,у₀).

Точка М₀(х₀,у₀) – центр окружности.

Для любой точки М(х;у), лежащей на окружности, расстояние ММ₀=R (R=const)

ММ₀==R

(х-х₀)²+(у-у₀)²=R²–(2)–уравнение окружности радиуса R с центром в точке М₀(х₀,у₀).

Параметрическое уравнение линии.

Пусть координаты х и у точек линии L выражаются при помощи параметра t:

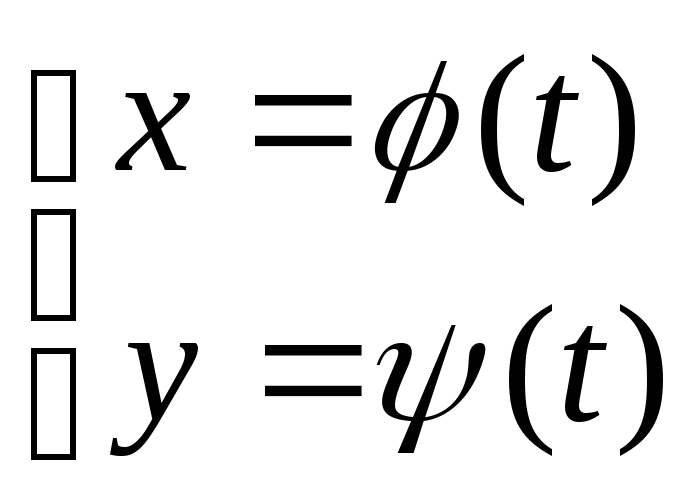(3) – параметрическое уравнение линии в ДСК

где функции (t) и (t) непрерывны по параметру t (в некоторой области изменения этого параметра).

Исключая из уравнения (3) параметр t, получим уравнение (1).

Рассмотрим линию L как путь, пройденный материальной точкой, непрерывно движущейся по определенному закону. Пусть переменная t представляет собой время, отсчитываемое от некоторого начального момента. Тогда задание закона движения представляет собой задание координат х и у движущейся точки как некоторых непрерывных функций х=(t) и у=(t) времени t.

Пример. Выведем параметрическое уравнение окружности радиуса r>0 с центром в начале координат. Пусть М(х,у) – произвольная точка этой окружности, а t – угол между радиус-вектором и осью Ох, отсчитываемый против часовой стрелки.

Тогда x=r cos x y=r sin t. (4)

У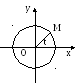равнения (4) представляют собой параметрические уравнения рассматриваемой окружности. Параметр t может принимать любые значения, но для того, чтобы точка М(х,у) один раз обошла окружность, область изменения параметра ограничивается полусегментом 0t2.

Возведя в квадрат и сложив уравнения (4), получим общее уравнение окружности (2).

2. Полярная система координат (пск).

Выберем на плоскости ось L (полярная ось) и определим точку этой оси О (полюс). Любая точка плоскости однозначно задается полярными координатами ρ и φ, где

ρ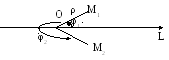 – полярный радиус, равный расстоянию от точки М до полюса О (ρ≥0);

φ[0;2Π] – угол между направлением вектора ОМ и осью L (полярный угол). М(ρ; φ)

Уравнение линии в ПСК может быть записано:

ρ=f(φ) (5) явное уравнение линии в ПСК

F=(ρ; φ) (6) неявное уравнение линии в ПСК

Связь между декартовыми и полярными координатами точки.

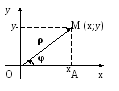(х;у) (ρ; φ) Из треугольника ОМА:

tg φ=(восстановление угла φ по известному тангенсу производится с учетом того, в каком квадранте находится точка М).(ρ; φ)(х;у). х=ρcos φ, y= ρsin φ

Пример. Найти полярные координаты точек М(3;4) и Р(1;-1).

Для М:=5, φ=arctg (4/3). Для Р: ρ=; φ=Π+arctg(-1)=3Π/4.

Классификация плоских линий.

Определение 1. Линия называется алгебраической, если в некоторой декартовой прямоугольной системе координат, если она определяется уравнением F(x;y)=0 (1), в котором функция F(x;y) представляет собой алгебраический многочлен.

Определение 2. Всякая не алгебраическая линия называется трансцендентной.

Определение 3. Алгебраическая линия называется линией порядка n, если в некоторой декартовой прямоугольной системе координат эта линия определяется уравнением (1), в котором функция F(x;y) представляет собой алгебраический многочлен n-й степени.

Т.о., линией n-го порядка называется линия, определяемая в некоторой декартовой прямоугольной системе алгебраическим уравнением степени n с двумя неизвестными.

Установлению корректности определений 1,2,3 способствует следующая теорема.

Теорема (док-во на с.107). Если линия в некоторой декартовой прямоугольной системе координат определяется алгебраическим уравнением степени n, то эта линия и в любой другой декартовой прямоугольной системе координат определяется алгебраическим уравнением той же степени n.