Выражение смешанного произведения через координаты векторов.

а=а_хi+a_yj+a_zk, b= b_хi+b_yj+b_zk, c= c_хi+c_yj+c_zk

abc=(a×b)c=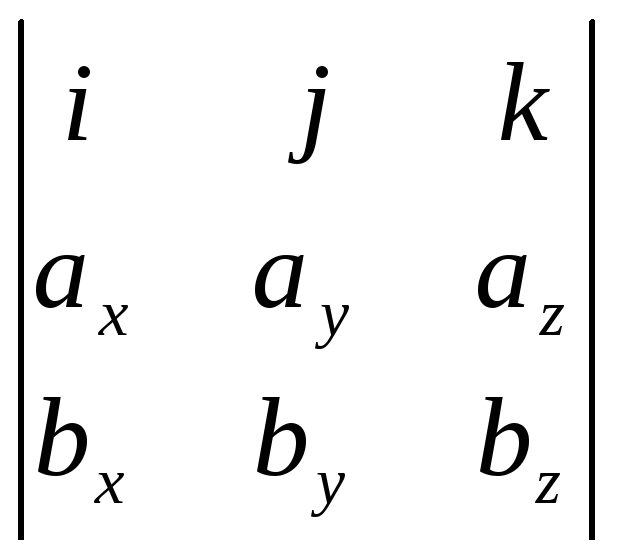(c_xi+c_yj+c_zk)=

=(i-j+k) (c_xi+c_yj+c_zk) =c_x-c_y+c_z

abc=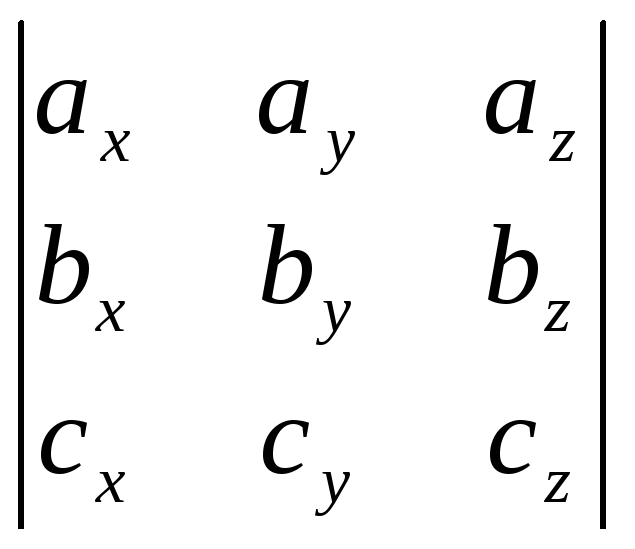

Т.о. объем параллелепипеда: V=±

V_пир.=S_{осн. пир.} Н= S_{осн. парал.}Н=±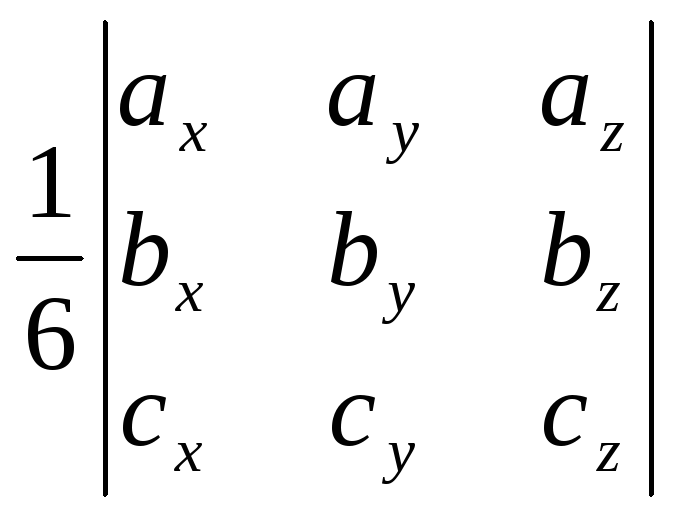

Следствие. Критерий компланарности: три вектора a,b и c компланарны тогда и только тогда, когда abc=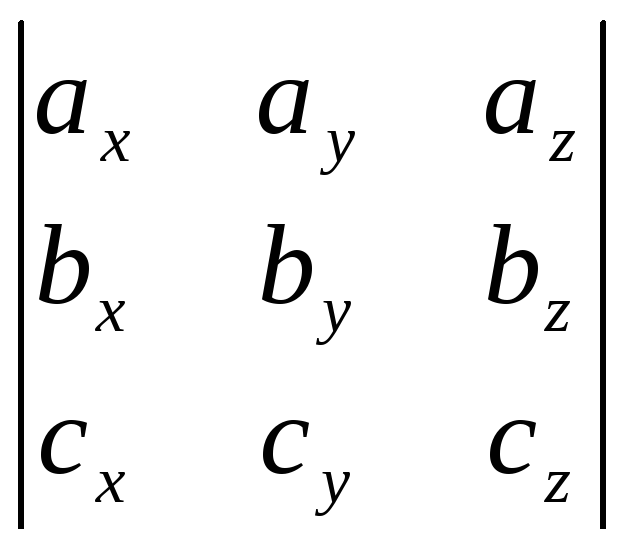=0 (в частности, любые два из них коллениарны).

Приложение смешанного произведения.

1. Определение ориентации тройки векторов. Если abc>0, то тройка векторов, которая его образует, является правой.

Если abc<0, то тройка векторов, которая его образует, является левой.

2. Определение компланарности векторов.

3. Вычисление объемов параллелепипеда и тетраэдра, построенного на векторах.

Пример. Определить ориентацию тройки векторов ijk.

ijk==1>0 – правая тройка векторов.

Двойное векторное произведение.

Пусть даны три произвольных вектора a, b и c. Если вектор b векторно умножается на вектор с, а вектор а также векторно умножается на векторное произведение bc, то полученный при этом вектор а(bc)=[a[bc]] называется двойным векторным произведением.

Теорема. (Док-во на с.79). Для любых векторов a, b и c справедлива формула:

а(bc)=[a[bc]]=b(ac)-c(ab) (13)

Из формулы (13)  (аb)c=[[ab]c]=b(ac)-a(bc) (13)

(Т.е. средний вектор, умноженный на скалярное произведение двух остальных, минус другой вектор внутреннего произведения, умноженный на скалярное произведение двух остальных.)