
- •Понятие базиса.
- •Проекция вектора на ось.
- •Свойства проекции вектора на ось.
- •Направляющие косинусы.
- •Скалярное произведение векторов.
- •Геометрические свойства скалярного произведения.
- •Алгебраические свойства скалярного произведения.
- •Выражение скалярного произведения через координаты векторов.
- •Векторное произведение векторов. Правые и левые тройки векторов и системы координат.
- •Геометрические свойства векторного произведения.
- •Геометрическое построение векторного произведения.
- •Выражение векторного произведения через координаты векторов.
- •Смешанное произведение векторов.
- •Геометрический смысл смешанного произведения.
- •Свойства смешанного произведения.
- •Выражение смешанного произведения через координаты векторов.
- •Приложение смешанного произведения.
Направляющие косинусы.
О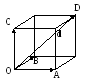 бозначим
буквами ,
,
углы наклона вектора
бозначим
буквами ,
,
углы наклона вектора
![]() к осям Ox,
Oy
и Oz
соответственно.
к осям Ox,
Oy
и Oz
соответственно.
Числа
cosα, cosβ, cosγ называются направляющими
косинусами вектора
![]() .
С учетом формулы
.
С учетом формулы
![]() и предыдущей теоремы, получаем формулы
для координат вектора
и предыдущей теоремы, получаем формулы
для координат вектора
![]() :
:
Х=![]()
cosα, Y=
cosα, Y=![]()
cosβ, Z=
cosβ, Z=![]()
cosγ (3)
cosγ (3)
Т.к.
квадрат диагонали прямоугольного
параллелепипеда равен сумме квадратов
его сторон, то из равенств ОА=Х, ОВ=Y,
OC=Z,
получим выражение для длины вектора
![]() :
:
![]() (4)
(4)
Из (3) и (4) получаем:
![]() ;
;
![]() ;
;
![]() (5)
(5)
Возводя в квадрат и складывая равенства (5), получаем:
cos2α+cos2β+cos2γ=1.
Т.к.
вектор
![]() однозначно определяется заданием
координат, то из (3) следует, что вектор
однозначно определяется заданием
координат, то из (3) следует, что вектор
![]() однозначно определяется заданием его
длины и направляющих
косинусов.
однозначно определяется заданием его
длины и направляющих
косинусов.
Действия над векторами.
![]() ={ах,ау,аz}={x,y,z}
={ах,ау,аz}={x,y,z}
Пусть
![]() ={х1,у1,z1},
={х1,у1,z1},
![]() ={х2,у2,z2},
={х2,у2,z2},
-
 =
=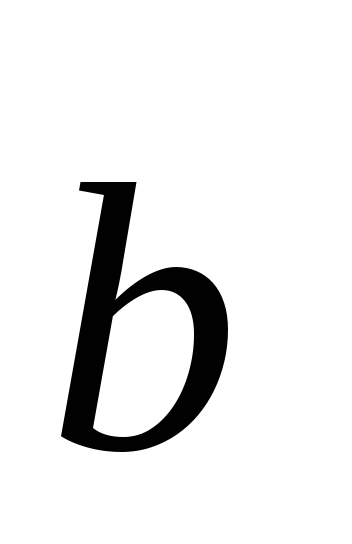 когда равны их соотв. координаты: х1=х2;
y1=y2;
z1=z2.
когда равны их соотв. координаты: х1=х2;
y1=y2;
z1=z2.
2)
Сумма (разность) векторов - вектор.
Пусть
![]() ,
,
![]() тогда
тогда
![]() ={х1+х2,у1+у2,z1+z2},
={х1+х2,у1+у2,z1+z2},
![]() ={х1-х2,у1-у2,z1-z2}.
={х1-х2,у1-у2,z1-z2}.
3)
Умножение вектора на число- вектор:
![]() ={λх1,λу1,λz1}.
={λх1,λу1,λz1}.
Примеры. а={2; -3;0}, b={1;3;-2}. a+2b={4;3;-4}.
.
Скалярное произведение векторов.
Определение 1. Скалярным произведением двух векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними:
![]() (1)
(1)
Рассмотрим
проекцию вектора
![]() на ось, определяемую вектором
на ось, определяемую вектором
![]() .
.
Тогда,
![]() (2)
(2)
Из
(1) и (2) следует:
![]() (3)
(3)
Аналогичным
образом получаем:
![]() (4)
(4)
Определение 2. Скалярным произведением двух векторов называется число, равное произведению длины одного из этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов.
Определения 1 и 2 эквивалентны.
Механический
смысл. Если
вектор
![]() изображает силу, точка приложения
которой перемещается
из начала в конец вектора
изображает силу, точка приложения
которой перемещается
из начала в конец вектора
![]() ,
то работа w
определяется равенством:
,
то работа w
определяется равенством:
w=![]() ,
т.е. равна скалярному произведению
векторов
,
т.е. равна скалярному произведению
векторов
![]() и
и
![]() .
.
Геометрические свойства скалярного произведения.
Если угол между двумя ненулевыми векторами прямой, то такие векторы называются ортогональными.
Теорема 1. Два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.
Доказательство.
Необходимость.
Пусть векторы
![]() и
и
![]() ортогональны,
- угол между ними. Тогда cos
=0
ортогональны,
- угол между ними. Тогда cos
=0![]() =0.
=0.
Достаточность.
Пусть
![]() =0.
Докажем, что векторы
=0.
Докажем, что векторы
![]() и
и
![]() ортогональны. Исключим тривиальный
случай, когда хотя бы один из векторов
ортогональны. Исключим тривиальный
случай, когда хотя бы один из векторов
![]() или
или
![]() равен 0. Если оба вектора ненулевые, то
равен 0. Если оба вектора ненулевые, то
![]() >0,
>0,
![]() >0из
равенства
>0из
равенства
![]() =0
и (1) следует, что cos
=0,
т.е. векторы
=0
и (1) следует, что cos
=0,
т.е. векторы
![]() и
и
![]() ортогональны. Ч.т.д.
ортогональны. Ч.т.д.
Теорема
2. Два ненулевых
вектора
![]() и
и
![]() составляют острый (тупой) угол тогда и
только тогда, когда их скалярное
произведение положительно (отрицательно).
составляют острый (тупой) угол тогда и
только тогда, когда их скалярное
произведение положительно (отрицательно).
Доказательство.
Т.к. векторы
![]() и
и
![]() ненулевые, то знак скалярного произведения
совпадает со знаком cos
.
Если угол
не превосходит ,
то cos
положителен тогда и только тогда, когда
- острый угол, и отрицателен тогда и
только тогда, когда
- тупой угол. Ч.т.д.
ненулевые, то знак скалярного произведения
совпадает со знаком cos
.
Если угол
не превосходит ,
то cos
положителен тогда и только тогда, когда
- острый угол, и отрицателен тогда и
только тогда, когда
- тупой угол. Ч.т.д.
Алгебраические свойства скалярного произведения.
-
аb=ba – свойство коммутативности.
-
 =
=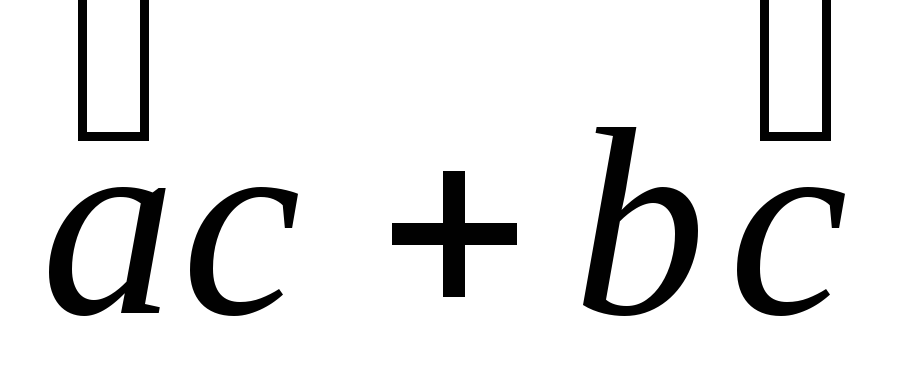 - дистрибутивное (распределительное)
относительно суммы векторов свойство.
- дистрибутивное (распределительное)
относительно суммы векторов свойство. -
 =
=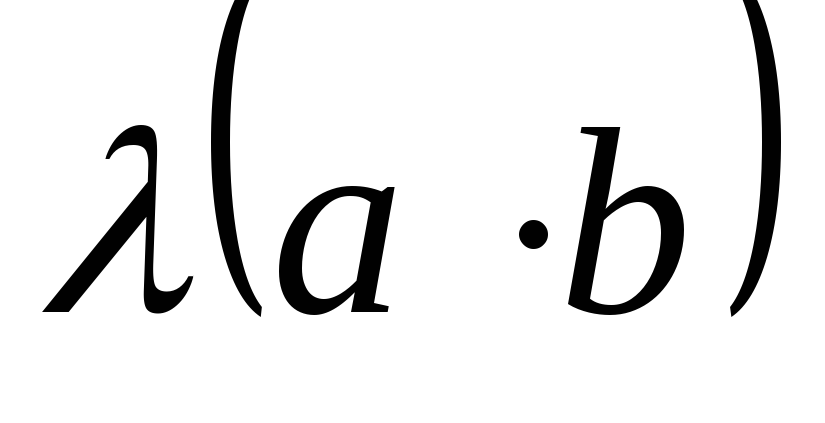 - сочетательное относительно скалярного
множителя свойство.
- сочетательное относительно скалярного
множителя свойство.
4) аа>0 если а ненулевой вектор, аа=0, если а – нулевой вектор.
Доказательства.
1) – следует из определения 1.
2)
– Воспользуемся формулой
![]() и линейным свойством проекции вектора
на ось.
и линейным свойством проекции вектора
на ось.
![]() =
=![]() =
=![]() =
=![]() +
+![]() =
=![]() .
.
3)
Аналогично св-ву 2):
![]() =
=![]() =
=![]() =
=![]() .
.
-
 -
скалярный квадрат вектора равен квадрату
его модуля. св-во
4.
-
скалярный квадрат вектора равен квадрату
его модуля. св-во
4.
